Optics (Ptolemy)


Ptolemy's Optics is a 2nd-century book on geometrical optics, dealing with reflection, refraction, and colour. The book was most likely written late in Ptolemy's life, after the Almagest, during the 160s.[1] The work is of great importance in the early history of optics. The Greek text has been lost completely. Fragments of the work survive only in the form of a Latin translation, prepared around 1154 by Eugene of Palermo, based on an Arabic translation which was presumably based on the Greek original. Both the Arabic and the Greek texts are lost entirely, and the Latin text is "badly mangled".[2] The Latin text was edited by Albert Lejeune in 1956. The 1996 English translation by Mark Smith is based on Lejeune's Latin text.
Textual history
[edit]The work is known to have been received by Arabic scholars working on optics in the 10th and 11th century, specifically Ibn Sahl (c. 984) and Ibn Al-Haytham (Alhazen), author of the influential Book of Optics (c. 1020). There are only three known references to the existence of the Greek text of the work, dated to the 4th, 6th and 11th centuries. The latest of these, produced by Simeon Seth, may however only be at second hand, so that it is uncertain whether the Greek text was still available in the medieval period, and the relation of the Arabic text available to Alhazen is unknown. On the other hand, the content of the Latin text produced by Eugene can to some extent be compared to the Arabic text available to Alhazen: both were structured in five books, and both are missing the first book entirely and the fifth book in part.[3] By contrast to the garbled state of the Arabic text and the complete loss of any Greek or Arabic manuscripts, the preservation of Eugene's Latin text is very good, the text being extant in 13 manuscripts, the oldest of which date to the early 14th century.[4]
Eugene's text was influential in the late medieval and Renaissance-era development of optics, even though its importance was overshadowed by the publication of the Latin translation of Alhazen's De aspectibus at the turn of the 13th century. Ptolemy's Optics is mentioned by Roger Bacon and Regiomontanus planned a printed edition (which was never published). The scientific progress made in the 16th and 17th centuries rendered the work so completely obsolete that it was considered a lost work by the mid-18th century. Manuscripts of the Latin text were recovered by philologists in the late 18th century, and in the 1820s there were once again preparations for the work's publication, which again came to nothing. A first edition finally appeared in 1885, prepared by Gilberto Govi. The first and still authoritative critical edition of the text is that of Lejeune, published in 1956.
Contents
[edit]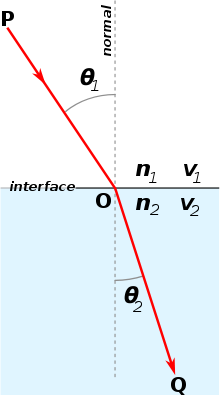
The work contains the earliest surviving table of refraction from air to water, for which the values (with the exception of the 60° angle of incidence), although historically praised as experimentally derived, appear to have been obtained from an arithmetic progression.[5]
However, according to Mark Smith, Ptolemy's tables were based on real experiments. His "adjustment" of the data, using arithmetic progression, is essentially the method of regularizing irregularly-changing values, which was often used by astronomers. This was done in order to organize and make sense of the tables' data in a rational way.[6]
Ptolemy also presents a theory of vision. In his view, rays (or flux) are emitted from the eye. The rays are sensitive, and convey information back to the observer's intellect about the distance and orientation of surfaces. Size and shape were determined by the visual angle subtended at the eye combined with perceived distance and orientation. This was one of the early statements of size-distance invariance as a cause of perceptual size and shape constancy, a view supported by the Stoics.[7]
Ptolemy offered explanations for many phenomena concerning illumination and colour, size, shape, movement and binocular vision. He also divided illusions into those caused by physical or optical factors and those caused by judgmental factors. He offered an obscure explanation of the sun or moon illusion (the enlarged apparent size on the horizon) based on the difficulty of looking upwards.[8][9]
See also
[edit]References
[edit]- ^ Smith 1996, p. 3.
- ^ Smith 1996, p. 5.
- ^ Smith (1996), p. 3, referencing Lejeune (1956), p. 27.
- ^ Lindberg 1975.
- ^ Boyer 1959.
- ^ Smith 2015, pp. 116–118.
- ^ Ross & Plug 1998.
- ^ Ross & Ross 1976, p. 377.
- ^ Sabra 1987.
Bibliography
[edit]- Boyer, Carl Benjamin (1959). The Rainbow: From Myth to Mathematics. New York: Thomas Yoseloff.
- Lejeune, Albert (1989) [first published in Louvrain, 1956]. L'Optique de Claude Ptolémée dans la version latine d'après l'arabe de l'émir Eugène de Sicile. Brill.
- Lindberg, David C. (1975). A Catalogue of Medieval and Renaissance Optical Manuscripts. Toronto.
{{cite book}}: CS1 maint: location missing publisher (link) - Ross, H.E.; Ross, G.M. (1976). "Did Ptolemy Understand the Moon Illusion?". Perception. 5 (4): 377–395. doi:10.1068/p050377. PMID 794813. S2CID 23948158.
- Sabra, A.I. (1987). "Psychology Versus Mathematics: Ptolemy and Alhazen on the Moon Illusion". In Grant, E.; Murdoch, J.E. (eds.). Mathematics and Its Application to Science and Natural Philosophy in the Middle Ages. Cambridge: Cambridge University Press. pp. 217–247.
- Ross, H.W.; Plug, C. (1998). "The History of Size Constancy and Size Illusions". In Walsh, V.; Kulikowski, J. (eds.). Perceptual Constancy: Why Things Look as They Do. Cambridge: Cambridge University Press. pp. 499–528.
- Smith, A. Mark (2015). From Sight to Light: The Passage from Ancient to Modern Optics. Chicago: The University of Chicago Press.
- Smith, A. Mark (1996). Ptolemy's Theory of Visual Perception– An English translation of the Optics. The American Philosophical Society. ISBN 0-87169-862-5.