Diagrama de Coxeter-Dynkin

En geometria, un diagrama de Coxeter-Dynkin (diagrama de Coxeter, o graf de Coxeter), nomenat així pels matemàtics Donald Coxeter i Eugene Dynkin, és un graf amb arestes etiquetades numèricament (anomenades «branques») que representen les relacions espacials entre una col·lecció de miralls (o hiperplans reflectits). Això descriu una construcció calidoscòpica: cada «node» del graf representa un mirall (anomenat faceta) i l'etiqueta enganxada a la branca codifica l'ordre de l'angle díedre entre dos miralls (en una cresta de domini). Una branca no marcada representa implícitament ordre-3.

Cada diagrama representa un grup de Coxeter, i els grups de Coxeter estan classificats pels seus diagrames associats.

Els diagrames de Dynkin estan estretament relacionats, però difereixen dels diagrames de Coxeter en dos aspectes:

• en primer lloc, les branques etiquetades com a «4» o més grans són dirigides, mentre que els diagrames de Coxeter no són dirigides;
• en segon lloc, els diagrames Dynkin han de satisfer una restricció (cristal·logràfica) addicional, és a dir, que les úniques branques permeses són les etiquetades com 2, 3, 4 i 6.

Els diagrames Dynkin es corresponen i s'utilitzen per classificar els sistemes d'arrels i, per tant, les àlgebres de Lie semisimple.^[1]

Les branques d'un diagrama de Coxeter-Dynkin estan etiquetades amb un nombre racional p, el que representa un angle diedre de 180°/p. Quan p = 2, l'angle és de 90° i els miralls no tenen cap interacció, de manera que la branca pot ser omesa del diagrama. Si una branca no està marcada, se suposa que té p = 3, el que representa un angle de 60°. Dos miralls paral·lels tenen una branca marcada amb «∞». En principi, n miralls poden ser representats per un graf complet en el qual es dibuixen totes les n(n - 1)/2 branques. A la pràctica, gairebé totes les configuracions interessants dels miralls inclouen una sèrie d'angles rectes, de manera que s'ometen les branques corresponents.

Els diagrames poden ser etiquetats per la seva estructura gràfica. Les primeres formes estudiades per Ludwig Schläfli són els ortoesquemes que tenen gràfics lineals que generen polítops regulars i tessel·lacions regulars. Els plagioesquemes són símplex representats pels grafs ramificats, i els cicloesquemes són símplex representats per grafs cicles.

Cada diagrama de Coxeter té una matriu de Schläfli corresponent amb elements de matriu a_i,j = a_j,i = -2cos (π / p), on p és l'ordre de la branca entre els parells de miralls. Com és una matriu de cosinus també s'anomena matriu de Gram. Totes les matrius de Schläfli del grup de Coxeter són simètriques perquè els seus vectors d'arrel estan normalitzats. Es relaciona estretament a la matriu de Cartan, que s'utilitza de forma similar, però els grafs dirigits dels diagrames de Dynkin estan limitats en els casos de p= 2, 3, 4 i 6, que en general NO són simètrics.

El determinant de la matriu de Schläfli, anomenat el Schläflià, i el seu signe determina si el grup és finit (positiu), afí (zero), indefinit (negatiu). Aquesta regla es denomina Criteri de Schläfli.^[2]

Els valors propis de la matriu de Schläfli determina si un grup de Coxeter és de tipus finit (tots positius), afí (tot no negatiu, almenys un és zero), o de tipus indefinit (en cas contrari). El tipus indefinit de vegades se subdivideix, per exemple, en grups de Coxeter hiperbòlics i altres. No obstant això, hi ha múltiples definicions no equivalents per als grups de Coxeter hiperbòlics. Utilitzem la següent definició: Un grup de Coxeter amb el diagrama connectat és hiperbòlic si no és ni de tipus finit ni afí, però cada subdiagrama apropiat connectat és de tipus finit o afí.

Un grup de Coxeter hiperbòlic és compacte si tots els subgrups són finits (és a dir, tenen determinants positius), i paracompacte si tots els seus subgrups són finits o afíns (és a dir, tenen determinants no negatius). Els grups finits i afins també s'anomenen el·líptics i parabòlics, respectivament. Els grups hiperbòlics també s'anomenen Lannér i F. Lannér, qui va enumerar els grups hiperbòlics compactes el 1950,^[3] i Koszul (o quasi-Lannér) per als grups paracompactes.

Pel rang 2, la varietat d'un grup de Coxeter està totalment determinada pel determinant de la matriu Schläfli, ja que és simplement el producte dels valors propis:

• tipus finit (determinant positiu),
• tipus afí (determinant igual a zero),
• tipus hiperbòlic (determinant negatiu).

Coxeter utilitza una notació gràfica equivalent, que enumera les seqüències de l'ordre de ramificació com un substitut dels diagrames de grafs amb nodes i branques. També hi ha solucions racionals ([p/q] o ), amb mcd (p, q) = 1, que defineixen la superposició de dominis fonamentals. Per exemple, 3/2, 4/3, 5/2, 5/3, 5/4 i 6/5.

Tipus	Finit					Afí	Hiperbòlic
Geometria					...
Coxeter	[ ]	[2]	[3]	[4]	[p]	[∞]	[∞]	[iπ/λ]
Ordre	2	4	6	8	2p	∞
Les línies de mirall són de color per correspondre als nodes del diagrama de Coxeter. Els dominis fonamentals estan acolorits alternativament.

Diagrames del grup Coxeter de rang 2

Ordre p	Grup	Diagrama de Coxeter		Matriu de Schläfli
				${\displaystyle \left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]}$	Determinant (4-a21*a₁₂)
Finit (Determinant > 0)
2	I₂(2) = A1xA1		[2]	${\displaystyle \left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]}$	4
3	I₂(3) = A₂		[3]	${\displaystyle \left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]}$	3
3/2			[3/2]	${\displaystyle \left[{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}\right]}$
4	I₂(4) = B₂		[4]	${\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {2}}\\-{\sqrt {2}}&2\end{smallmatrix}}\right]}$	2
4/3			[4/3]	${\displaystyle \left[{\begin{smallmatrix}2&{\sqrt {2}}\\{\sqrt {2}}&2\end{smallmatrix}}\right]}$
5	I₂(5) = H₂		[5]	${\displaystyle \left[{\begin{smallmatrix}2&-\phi \\-\phi &2\end{smallmatrix}}\right]}$	${\displaystyle (5-{\sqrt {5}})/2}$ ~1.38196601125
5/4			[5/4]	${\displaystyle \left[{\begin{smallmatrix}2&\phi \\\phi &2\end{smallmatrix}}\right]}$
5/2			[5/2]	${\displaystyle \left[{\begin{smallmatrix}2&1-\phi \\1-\phi &2\end{smallmatrix}}\right]}$	${\displaystyle (5+{\sqrt {5}})/2}$ ~3.61803398875
5/3			[5/3]	${\displaystyle \left[{\begin{smallmatrix}2&\phi -1\\\phi -1&2\end{smallmatrix}}\right]}$
6	I₂(6) = G₂		[6]	${\displaystyle \left[{\begin{smallmatrix}2&-{\sqrt {3}}\\-{\sqrt {3}}&2\end{smallmatrix}}\right]}$	1
6/5			[6/5]	${\displaystyle \left[{\begin{smallmatrix}2&{\sqrt {3}}\\{\sqrt {3}}&2\end{smallmatrix}}\right]}$
8	I₂(8)		[8]	${\displaystyle \left[{\begin{smallmatrix}2&-2\cos(\pi /8)\\-2\cos(\pi /8)&2\end{smallmatrix}}\right]}$	${\displaystyle 2-{\sqrt {2}}}$ ~0.58578643763
10	I₂(10)		[10]	${\displaystyle \left[{\begin{smallmatrix}2&-2\cos(\pi /10)\\-2\cos(\pi /10)&2\end{smallmatrix}}\right]}$	${\displaystyle 4\sin ^{2}(\pi /10)}$ =${\displaystyle (3-{\sqrt {5}})/2}$ ~0.38196601125
12	I₂(12)		[12]	${\displaystyle \left[{\begin{smallmatrix}2&-2\cos(\pi /12)\\-2\cos(\pi /12)&2\end{smallmatrix}}\right]}$	${\displaystyle 2-{\sqrt {3}}}$ ~0.26794919243
p	I₂(p)		[p]	${\displaystyle \left[{\begin{smallmatrix}2&-2\cos(\pi /p)\\-2\cos(\pi /p)&2\end{smallmatrix}}\right]}$	${\displaystyle 4\sin ^{2}(\pi /p)}$
Afí (Determinant = 0)
∞	I₂(∞) = ${\displaystyle {\tilde {I}}_{1}}$ = ${\displaystyle {\tilde {A}}_{1}}$		[∞]	${\displaystyle \left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]}$	0
Hiperbòlic (Determinant ≤ 0)
∞			[∞]	${\displaystyle \left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]}$	0
∞			[iπ/λ]	${\displaystyle \left[{\begin{smallmatrix}2&-2cosh(2\lambda )\\-2cosh(2\lambda )&2\end{smallmatrix}}\right]}$	${\displaystyle -4\sinh ^{2}(2\lambda )\leq 0}$

El diagrama de Coxeter-Dynkin pot ser vist com un graf descriptiu del domini fonamental dels miralls. Un mirall representa un hiperplà en un espai esfèric, euclidià, o en un espai hiperbòlic; (en els espais 2D un mirall és una línia, i en 3D un mirall és un pla).

Aquestes visualitzacions mostren els dominis fonamentals dels grups euclidians 2D i 3D, i dels grups esfèrics 2D. Per a cada diagrama de Coxeter es pot deduir mitjançant la identificació els miralls hiperplans i l'etiquetatge de les seves connectivitats, fent cas omís dels angles diedres de 90° (ordre 2).

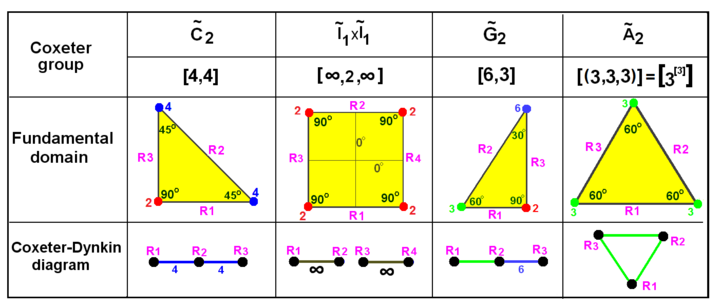Grups de Coxeter en el pla euclidià amb els diagrames equivalents. Les reflexions estan etiquetades en els nodes del graf, R1, R2, etc., i estan acolorides pel seu ordre reflexió. Les reflexions de 90° estan inactives, i per tant suprimides del diagrama. Els miralls paral·lels estan connectats per la branca etiquetada amb ∞. El grup prismàtic ${\displaystyle {\tilde {I}}_{1}}$x ${\displaystyle {\tilde {I}}_{1}}$es mostra com una duplicació de ${\displaystyle {\tilde {C}}_{2}}$, però també es pot crear com a domini rectangular de la duplicació dels triangles ${\displaystyle {\tilde {G}}_{2}}$. ${\displaystyle {\tilde {A}}_{2}}$ és una duplicació del triangle ${\displaystyle {\tilde {G}}_{2}}$.
Molts grups de Coxeter en el pla hiperbòlic es poden estendre a partir dels casos euclidians com una sèrie de solucions hiperbòliques.
Grups de Coxeter en espai 3D amb diagrames. Els miralls (cares triangulars) són etiquetats per 0..3 al vèrtex oposat. Les branques s'acoloreixen pel seu ordre reflexió. ${\displaystyle {\tilde {C}}_{3}}$ omplert amb un 1/48 de cub. ${\displaystyle {\tilde {B}}_{3}}$ omplert amb 1/24 de cub. ${\displaystyle {\tilde {A}}_{3}}$ omplert amb 1/12 de cub.	Grups de Coxeter en l'esfera amb diagrames equivalents. Un domini fonamental es resumeix en groc. Els vèrtexs del domini (i les branques del graf) s'acoloreixen pel seu ordre reflexió.

Vegeu també famílies de polítops per a una taula de polítops uniformes de node final associats amb aquests grups.

• Es donen tres símbols diferents per als mateixos grups; una lletra / nombre, un conjunt de nombres entre claudàtors, i el diagrama de Coxeter.
• Els grups D_n bifurcats són la meitat o la versió alternada dels grups regulars C_n.
• Els grups D_n i E_n bifurcats també són etiquetats amb una forma superíndexada [3^a,b,c], on a, b, c són els números de segments en cadascuna de les tres branques.

Grafs de Dynkin connectats fins a (rangs d'1 a 9)

Rang	Grups de Lie simple			Grups de Lie excepcionals
	${\displaystyle {A}_{1+}}$	${\displaystyle {B}_{2+}}$	${\displaystyle {D}_{2+}}$	${\displaystyle {E}_{3-8}}$	${\displaystyle {F}_{3-4}}$	${\displaystyle {G}_{2}}$	${\displaystyle {H}_{2-4}}$	${\displaystyle {I}_{2}(p)}$
1	A1=[ ]
2	A₂=[3]	B₂=[4]	D₂=A1A1			G₂=[6]	H₂=[5]	I₂[p]
3	A₃=[3²]	B₃=[3,4]	D₃=A₃	E₃=A₂A1	F₃=B₃		H₃
4	A₄=[33]	B₄=[3²,4]	D₄=[31,1,1]	E₄=A₄	F₄		H₄
5	A₅=[34]	B₅=[33,4]	D₅=[32,1,1]	E₅=D₅
6	A₆=[3⁵]	B₆=[34,4]	D₆=[33,1,1]	E₆=[32,2,1]
7	A₇=[3⁶]	B₇=[3⁵,4]	D₇=[34,1,1]	E₇=[33,2,1]
8	A₈=[37]	B₈=[3⁶,4]	D₈=[35,1,1]	E₈=[34,2,1]
9	A9=[38]	B9=[37,4]	D9=[36,1,1]
10+	..	..	..	..

En la construcció de polítops uniformes, els nodes es marquen com «actius» amb un anell si un punt generador està fora del mirall, creant una nova vora entre el punt generador i la seva imatge especular. Un node sense anell representa un mirall inactiu que no genera nous punts.

Dos miralls ortogonals es poden utilitzar per generar un quadrat, , vist aquí amb un punt de generador en vermell i 3 còpies virtuals a través dels miralls. El generador ha de ser de tots dos miralls, en aquest cas ortogonal, per generar a l'interior. Els punts marcats amb anells se suposa que són generadors actius que tenen la mateixa distància de tots els miralls, mentre que un rectangle també es pot representar una solució uniforme.

Els diagrames de Coxeter-Dynkin poden enumerar explícitament gairebé totes les classes de polítops uniformes i mosaics uniformes. Cada polítop uniforme amb simetria de reflexió pura (tots, excepte uns pocs casos especials, tenen simetria de reflexió pura) pot ser representat per un diagrama de Coxeter-Dynkin amb permutacions de marques. Cada polítop uniforme pot ser generat utilitzant aquest tipus de miralls i un únic punt generador; les imatges del mirall creen nous punts com reflexos, i llavors els polítops arestes poden ser definits entre els punts i un punt de la imatge del mirall. Les cares poden ser construïdes per cicles d'arestes creades, etc. Per especificar la generació del vèrtex, un o més nodes estan marcats amb els anells, el que significa que el vèrtex no està dins del mirall(s), representat per node(s) amb anell(s); si dos o més miralls estan marcats, el vèrtex és equidistant a ells. Un mirall és actiu (crea reflexions) només pel que fa als punts, no en ell. Un diagrama necessita almenys un node actiu per representar un polítop.

Tots els polítops regulars, representats pel símbol de Schläfli {p, q, r, ...}, poden tenir els seus dominis fonamentals representats per un conjunt de n miralls relacionats amb un diagrama de Coxeter-Dynkin d'una línia de nodes i branques etiquetades per p, q, r, ..., amb el primer node anellat.

Els polítops uniformes amb un anell corresponen al generador de punts en els cantons del domini fonamental símplex. Dos anells corresponen a les arestes del símplex i tenen un grau de llibertat, amb només el punt mitjà com la solució uniforme per a la mateixa longitud de l'aresta. En general, el generador de punts de k-anells estan en (k-1)-cares del símplex, i si tots el nodes estan anellats, el punt generador està a l'interior del símplex.

Un marcat secundari transmet un cas especial de polítops uniformes amb simetria no-reflectiva. Aquests casos existeixen com a alternatives de polítops de simetria de reflexió. Aquest marcat elimina el punt central d'un node anellat, anomenat «forat» (cercles amb nodes esborrats), que dona a entendre que els nodes alternatius han sigut eliminats. El polítop resultant tindrà una subsimetria del grup de Coxeter original. Una truncació alternada s'anomena «xato».

• Un únic node representa un sol mirall; això s'anomena grup A₁. Si el node amb anell crea un segment lineal perpendicular al mirall, es representa com {}.
• Dos nodes no units representen dos miralls perpendiculars. Si tots dos nodes tenen un anell es pot crear un rectangle, o un quadrat si el punt està a la mateixa distància de tots dos miralls.
• Dos nodes connectats per una branca d'ordre n pot crear un n-gon si el punt està en un mirall, i un 2n-gon si el punt està fora de tots dos miralls. Això forma el grup I₁ (n).
• Dos miralls paral·lels poden representar un polígon infinit, formant el grup I₁ (∞), també anomenat Ĩ_1.
• Tres miralls en triangle formen imatges vistes en un calidoscopi tradicional i es poden representar per tres nodes connectats a un triangle. Repetint aquest model s'obtenen branques etiquetades com (3 3 3), (4 4 2), (3 2 6), encara que els dos últims es poden dibuixar com una línia (amb les dues branques ignorades). Aquestes generaran tessel·lats regulars.
• Tres miralls poden generar políedres uniformes; inclosos els nombres racionals dona el conjunt de triangles de Schwarz.
• Tres miralls, amb un perpendicular als altres dos, poden formar els prismes regulars.

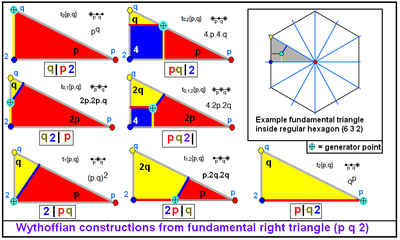En general, hi ha 7 construccions uniformes reflectores dins d'un triangle, a partir de 7 posicions topològiques del generador dins el domini fonamental. Cada mirall actiu té un generador en un vèrtex, amb dos miralls actius es tenen generadors en els costats, i tres miralls actius es té el generador a l'interior. Es poden resoldre un o dos graus de llibertat per una posició única per a longituds de les arestes del poliedre resultant o de la tessel·lació.

Exemple 7 generadors en simetria octaèdrica, domini fonamental del triangle (4 3 2), amb generació d'1/8 xato com una alternança.

De vegades, els polítops uniformes dobles es marquen amb una barra perpendicular en substitució del nodes anellats, i una barra per als forats del nodes xatos. Per exemple, representa un rectangle (com dos miralls ortogonals actius), i representa el seu polígon dual, el rombe.

Per exemple, el grup Coxeter B₃ té un diagrama  ; això també es diu simetria octaèdrica.

Hi ha 7 políedres uniformes convexes que es poden construir a partir d'aquest grup de simetria i 3 a partir de les seves subsimetries de les seves alternances, cada un amb un diagrama de Coxeter-Dynkin marcat de manera única cap amunt. El símbol de Wythoff representa un cas especial del diagrama de Coxeter de grafs de rang 3, amb totes les branques d'ordre 3 etiquetades, en lloc de suprimir les banques d'ordre 2. El símbol de Wythoff és capaç de manejar la forma xata, però no les alternances generals i sense tots els nodes anellats.

Políedres octaèdrics uniformes
Simetria: [4,3], (*432)							[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=				= or	= or	=
Duals de políedres uniformes
V43	V3.8²	V(3.4)²	V4.6²	V34	V3.43	V4.6.8	V34.4	V33	V3.6²	V3⁵

Les mateixes construccions es poden fer en grups de Coxeter inconnexos (ortogonals) com els prismes uniformes, i es pot veure més clarament com mosaics de diedres i hosohedres sobre l'esfera, com la família [6] × [ ] o [6,2] :

Políedres esfèrics diedres hexagonals uniformes
Simetria: [6,2], (*622)							[6,2]+, (622)	[6,2+], (2*3)
{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	s{2,6}
Duals dels políedres uniformes
V6²	V12²	V6²	V4.4.6	V2⁶	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

En comparació, la família [6,3], produeix un conjunt paral·lel de 7 tessel·lats uniformes del pla euclidià i el seu tessel·lat dual. També en aquest cas hi ha 3 alternances i alguna versió de mitja simetria.

Políedres hexagonals uniformes / Tessel·lats triangulars
Simetria: [6,3], (*632)							[6,3]+ (632)	[6,3+] (3*3)
{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}	s{3,6}
63	3.12²	(3.6)²	6.6.6	3⁶	3.4.12.4	4.6.12	3.3.3.3.6	3.3.3.3.3.3
Duals dels políedres uniformes
V63	V3.12²	V(3.6)²	V63	V3⁶	V3.4.12.4	V.4.6.12	V34.6	V3⁶

En el pla hiperbòlic [7,3], la família produeix un conjunt paral·lel de tessel·lats uniformes del pla euclidià i el seu tessel·lat dual. Només ha 1 alternança (xata), ja que tots els ordres de ramificació són imparells. Moltes altres famílies hiperbòliques dels tessel·lats uniformes es poden veure en els tessel·lats uniformes en pla hiperbòlic.

Políedres heptagonals uniformes / Tessel·lats triangulars
Simetria: [7,3], (*732)							[7,3]+, (732)
{7,3}	t{7,3}	r{7,3}	t{3,7}	{3,7}	rr{7,3}	tr{7,3}	sr{7,3}
Duals dels políedres uniformes
V73	V3.14.14	V3.7.3.7	V6.6.7	V37	V3.4.7.4	V4.6.14	V3.3.3.3.7

Les famílies del tessel·lats euclidians convexos regulars es defineixen pels grups de Coxeter afins. Aquests grups són idèntics als grups finits amb la inclusió d'un node afegit. Els nom de les lletres se'ls dona la mateixa lletra amb un ~ per sobre de la lletra. L'índex es refereix al grup finit, de manera que el rang és l'índex més 1 (els símbols d'Ernst Witt per als grups afins es donen com «també» entre parèntesis).

1. ${\displaystyle {\tilde {A}}_{n-1}}$: els diagrames d'aquest tipus són cicles. (també P_n)
2. ${\displaystyle {\tilde {C}}_{n-1}}$ : està associat amb la família de tessel·lació hipercúbica regular {4, 3, ...., 4}. (també R_n)
3. ${\displaystyle {\tilde {B}}_{n-1}}$ : relacionats amb C per un mirall eliminat. (també S_n)
4. ${\displaystyle {\tilde {D}}_{n-1}}$ : relacionats amb C per dos miralls eliminats. (també Q_n)
5. ${\displaystyle {\tilde {E}}_{6}}$, ${\displaystyle {\tilde {E}}_{7}}$, ${\displaystyle {\tilde {E}}_{8}}$. (també T₇, T₈, T₉)
6. ${\displaystyle {\tilde {F}}_{4}}$ : formes de la tessel·lació regular {3,4,3,3}. (també U₅)
7. ${\displaystyle {\tilde {G}}_{2}}$ : formes del domini fonamental del triangle 30-60-90. (també V₃)
8. ${\displaystyle {\tilde {I}}_{1}}$ : són dos miralls paral·lels. (= ${\displaystyle {\tilde {A}}_{1}}$ = ${\displaystyle {\tilde {C}}_{1}}$) (també W₂)

Els grups compostos també es poden definir com a projeccions ortogonals. L'ús més comú ${\displaystyle {\tilde {A}}_{1}}$, com ${\displaystyle {\tilde {A}}_{1}^{2}}$ representa els dominis d'un tauler d'escacs quadrat o rectangular al pla euclidià. ${\displaystyle {\tilde {A}}_{1}{\tilde {G}}_{2}}$ representa els dominis fonamentals del prisma triangular en el 3-espai euclidià.

Grafs de Coxeters afins (de 2 a 10 nodes)

Rang	${\displaystyle {\tilde {A}}_{1+}}$ (P2+)	${\displaystyle {\tilde {B}}_{3+}}$ (S4+)	${\displaystyle {\tilde {C}}_{1+}}$ (R2+)	${\displaystyle {\tilde {D}}_{4+}}$ (Q5+)	${\displaystyle {\tilde {E}}_{n}}$ (Tn+1) / ${\displaystyle {\tilde {F}}_{4}}$ (U₅) / ${\displaystyle {\tilde {G}}_{2}}$ (V₃)
2	${\displaystyle {\tilde {A}}_{1}}$=[∞]		${\displaystyle {\tilde {C}}_{1}}$=[∞]
3	${\displaystyle {\tilde {A}}_{2}}$=[3[3]] *		${\displaystyle {\tilde {C}}_{2}}$=[4,4] *		${\displaystyle {\tilde {G}}_{2}}$=[6,3] *
4	${\displaystyle {\tilde {A}}_{3}}$=[3[4]] *	${\displaystyle {\tilde {B}}_{3}}$=[4,31,1] *	${\displaystyle {\tilde {C}}_{3}}$=[4,3,4] *	${\displaystyle {\tilde {D}}_{3}}$=[31,1,3−1,31,1] = ${\displaystyle {\tilde {A}}_{3}}$
5	${\displaystyle {\tilde {A}}_{4}}$=[3[5]] *	${\displaystyle {\tilde {B}}_{4}}$=[4,3,31,1] *	${\displaystyle {\tilde {C}}_{4}}$=[4,3²,4] *	${\displaystyle {\tilde {D}}_{4}}$=[31,1,1,1] *	${\displaystyle {\tilde {F}}_{4}}$=[3,4,3,3] *
6	${\displaystyle {\tilde {A}}_{5}}$=[3[6]] *	${\displaystyle {\tilde {B}}_{5}}$=[4,3²,31,1] *	${\displaystyle {\tilde {C}}_{5}}$=[4,33,4] *	${\displaystyle {\tilde {D}}_{5}}$=[31,1,3,31,1] *
7	${\displaystyle {\tilde {A}}_{6}}$=[3[7]] *	${\displaystyle {\tilde {B}}_{6}}$=[4,33,31,1]	${\displaystyle {\tilde {C}}_{6}}$=[4,34,4]	${\displaystyle {\tilde {D}}_{6}}$=[31,1,3²,31,1]	${\displaystyle {\tilde {E}}_{6}}$=[32,2,2]
8	${\displaystyle {\tilde {A}}_{7}}$=[3[8]] *	${\displaystyle {\tilde {B}}_{7}}$=[4,34,31,1] *	${\displaystyle {\tilde {C}}_{7}}$=[4,3⁵,4]	${\displaystyle {\tilde {D}}_{7}}$=[31,1,33,31,1] *	${\displaystyle {\tilde {E}}_{7}}$=[33,3,1] *
9	${\displaystyle {\tilde {A}}_{8}}$=[3[9]] *	${\displaystyle {\tilde {B}}_{8}}$=[4,3⁵,31,1]	${\displaystyle {\tilde {C}}_{8}}$=[4,3⁶,4]	${\displaystyle {\tilde {D}}_{8}}$=[31,1,34,31,1]	${\displaystyle {\tilde {E}}_{8}}$=[35,2,1] *
10	${\displaystyle {\tilde {A}}_{9}}$=[3[10]] *	${\displaystyle {\tilde {B}}_{9}}$=[4,3⁶,31,1]	${\displaystyle {\tilde {C}}_{9}}$=[4,37,4]	${\displaystyle {\tilde {D}}_{9}}$=[31,1,3⁵,31,1]
11	...	...	...	...

Hi ha molts grups de Coxeter hiperbòlics infinits. Els grups hiperbòlics es classifiquen en compactes o no, amb els grups compactes que tenen dominis fonamentals delimitats. Existeixen grups hiperbòlics compactes símplex (Lannér símplex) amb rang de 3 a 5. Els grups paracompactes símplex (Koszul símplex) existeixen fins al rang 10. Els grups supercompactes (polítops Vinberg) han estat explorats però encara no s'han determinat totalment. En 2006, Allcock va demostrar que hi ha un nombre infinit de polítops Vinberg compactes per dimensions superiors a 6, i un nombre infinit de volums finits per politops Vinberg per a dimensions superiors a 19,^[4] pel que una enumeració completa no és possible. Tots aquests dominis reflectants fonamentals, tant símplex com no-símplex, es solen anomenar «politops Coxeter» o, de vegades amb menys precisió, «políedres Coxeter».

Disc de Poincaré de domini fonamental triangular

Exemple de triangles rectangles [p,q]
[3,7]	[3,8]	[3,9]	[3,∞]
[4,5]	[4,6]	[4,7]	[4,8]	[∞,4]
[5,5]	[5,6]	× × €4.95 / month Favourites List Audio Listining Color Mode Monthly New Updates Fullname * Email * Credit or debit card Subscribe A PHP Error was encountered Severity: Notice Message: Undefined variable: userid Filename: user/popup_modal.php Line Number: 68 Backtrace: File: /var/www/wikizero/data/www/wikizero.com/application/views/user/popup_modal.php Line: 68 Function: _error_handler File: /var/www/wikizero/data/www/wikizero.com/application/views/page/index.php Line: 478 Function: view File: /var/www/wikizero/data/www/wikizero.com/application/controllers/Main.php Line: 107 Function: view File: /var/www/wikizero/data/www/wikizero.com/index.php Line: 315 Function: require_once "> Subscribe Now × €4.95 € 9.90 / Modal title × Close Save changes × Diagrama_de_Coxeter-Dynkin" id="cancelSubscription" name="cancelSubscription" class="mb-0"> A PHP Error was encountered Severity: Notice Message: Undefined variable: user_membership Filename: user/popup_modal.php Line Number: 192 Backtrace: File: /var/www/wikizero/data/www/wikizero.com/application/views/user/popup_modal.php Line: 192 Function: _error_handler File: /var/www/wikizero/data/www/wikizero.com/application/views/page/index.php Line: 478 Function: view File: /var/www/wikizero/data/www/wikizero.com/application/controllers/Main.php Line: 107 Function: view File: /var/www/wikizero/data/www/wikizero.com/index.php Line: 315 Function: require_once A PHP Error was encountered Severity: Warning Message: Invalid argument supplied for foreach() Filename: user/popup_modal.php Line Number: 192 Backtrace: File: /var/www/wikizero/data/www/wikizero.com/application/views/user/popup_modal.php Line: 192 Function: _error_handler File: /var/www/wikizero/data/www/wikizero.com/application/views/page/index.php Line: 478 Function: view File: /var/www/wikizero/data/www/wikizero.com/application/controllers/Main.php Line: 107 Function: view File: /var/www/wikizero/data/www/wikizero.com/index.php Line: 315 Function: require_once A PHP Error was encountered Severity: Notice Message: Undefined variable: userid Filename: user/popup_modal.php Line Number: 208 Backtrace: File: /var/www/wikizero/data/www/wikizero.com/application/views/user/popup_modal.php Line: 208 Function: _error_handler File: /var/www/wikizero/data/www/wikizero.com/application/views/page/index.php Line: 478 Function: view File: /var/www/wikizero/data/www/wikizero.com/application/controllers/Main.php Line: 107 Function: view File: /var/www/wikizero/data/www/wikizero.com/index.php Line: 315 Function: require_once "> Harry Potter Books × A PHP Error was encountered Severity: Notice Message: Undefined variable: products Filename: user/popup_harry_book.php Line Number: 24 Backtrace: File: /var/www/wikizero/data/www/wikizero.com/application/views/user/popup_harry_book.php Line: 24 Function: _error_handler File: /var/www/wikizero/data/www/wikizero.com/application/views/page/index.php Line: 479 Function: view File: /var/www/wikizero/data/www/wikizero.com/application/controllers/Main.php Line: 107 Function: view File: /var/www/wikizero/data/www/wikizero.com/index.php Line: 315 Function: require_once A PHP Error was encountered Severity: Warning Message: Invalid argument supplied for foreach() Filename: user/popup_harry_book.php Line Number: 24 Backtrace: File: /var/www/wikizero/data/www/wikizero.com/application/views/user/popup_harry_book.php Line: 24 Function: _error_handler File: /var/www/wikizero/data/www/wikizero.com/application/views/page/index.php Line: 479 Function: view File: /var/www/wikizero/data/www/wikizero.com/application/controllers/Main.php Line: 107 Function: view File: /var/www/wikizero/data/www/wikizero.com/index.php Line: 315 Function: require_once