Diagrama de Hasse

En matemàtiques, un diagrama de Hasse és una representació gràfica simplificada d'un conjunt parcialment ordenat finit. Això s'aconsegueix eliminant informació redundant. Per a això es dibuixa una aresta ascendent entre dos elements només si un segueix a un altre sense haver altres elements intermedis.

En un diagrama de Hasse s'elimina la necessitat de representar:

• Cicles d'un element, ja que s'entén que una relació d'ordre parcial és reflexiva.
• Arestes que es dedueixen de la transitivitat de la relació.

• De dos membres x i y d'un conjunt parcialment ordenat S que « y segueix x » si x ≤ y i no hi ha element de S entre x i y.

L'ordre parcial és llavors precisament la clausura transitiva de la relació de seguir .

• El diagrama de Hasse de S es defineix com el conjunt de tots els parells ordenats ( x , y ) tals que y segueix x , és a dir, el diagrama de Hasse es pot identificar amb la relació de seguir .

Concretament, es representa cada membre de S com un punt negre a la pàgina i es dibuixa una línia que vagi cap amunt de x a y si y segueix x.

Per exemple, sigui el conjunt A ={1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}(tots els divisors de 60). Aquest conjunt està ordenat parcialment per la relació de divisibilitat. El seu diagrama de Hasse pot ser representat de la manera següent:

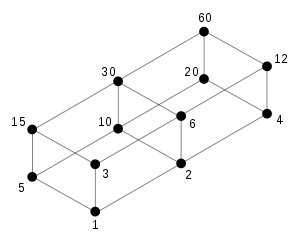
Per exemple, en el diagrama de Hasse del Poset de tots els divisors d'un nombre n , ordenats parcialment per divisibilitat, n mateix està en el límit del diagrama, el número 1 estaria en el fons, i els divisors més petits (cosins) seguirien l'element inferior.

Un diagrama de Hasse es pot veure també com un graf al qual se li lleven tots els seus bucles i els seus arestes que poden deduir amb la propietat transitiva i propietat reflexiva.

Les relacions «seguir» queda definida de manera única a partir de la relació d'ordre inicial. Això fa que les arestes del diagrama de Hasse i els punts que connecten quedin determinats també de forma única. Però hi ha un problema addicional: trobar una ubicació adequada per als vèrtexs que pugui reflectir alguna de les simetries subjacents. En aquest sentit, trobar un bon diagrama és difícil.

S'han proposat diversos algorismes per a dibuix de «bons» diagrames, però avui dia la seva construcció segueix basant-se en una forta intervenció humana. De fet, fins i tot un humà necessita bastant pràctica per elaborar-los.

Els següents exemples corresponen a diagrames de Hasse d'una mateixa relació d'ordre:

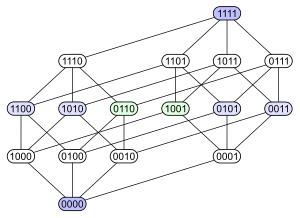A Wikimedia Commons hi ha contingut multimèdia relatiu a: Diagrama de Hasse