Processament de senyals

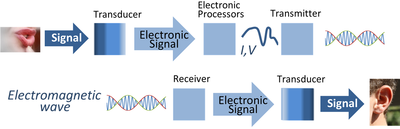
El processament de senyals (també anomenat tractament de senyals) és un subcamp d’enginyeria elèctrica que se centra a analitzar, modificar i sintetitzar senyals com ara so, imatges i mesures científiques.[1] Les tècniques de processament del senyal es poden utilitzar per millorar la transmissió, l'eficiència de l'emmagatzematge i la qualitat subjectiva i també per emfatitzar o detectar components d’interès en un senyal mesurat.[2]
És la disciplina que desenvolupa i estudia les tècniques de tractament (filtratge, amplificació, ...), d'anàlisi i d'interpretació dels senyals, tant en senyals continus (Processament analògic de senyals) com senyals discrets (Processament digital de senyals). Utilitza, doncs, els resultats de la teoria de la informació, de l'estadística i la matemàtica aplicada.[3] Exemples en què se sol utilitzar el processament de senyals és en la transmissió de senyals com ara la ràdio, en enregistrar so (com ara música), en imatges...[1]
Els senyals que poden ésser tractats poden provenir de fonts molt diverses, tot i que, majoritàriament, es tracta de senyals elèctrics, o que han estat convertits en elèctrics mitjançant captadors i transductors.
Història
[modifica]Segons Alan V. Oppenheim i Ronald W. Schafer, els principis del processament del senyal es poden trobar a les tècniques d’anàlisi numèrica clàssica del segle xvii. A més, afirmen que el refinament digital d’aquestes tècniques es pot trobar en els sistemes de control digital dels anys quaranta i cinquanta.[4]
El 1948, Claude Shannon va escriure l'influent article "A Mathematical Theory of Communication" que es va publicar al Bell System Technical Journal.[5] El document va establir les bases per al desenvolupament posterior de sistemes de comunicació d'informació i el processament de senyals per a la transmissió.[6]
El processament del senyal va madurar i va prosperar als anys seixanta i setanta, i el processament digital del senyal es va utilitzar àmpliament als anys vuitanta amb xips especialitzats processadors digitals de senyals.[6]
Tipus de senyals
[modifica]Els senyals poden ésser analògics i digitals. Els primers poden provenir de captadors (o captadors+transductors) com ara un micròfon (que capta sons), una sonda termomètrica (que capta temperatures), una sonda baromètrica (que capta pressions), un velocímetre, un acceleròmetre, etc. Els senyals analògics es caracteritzen per representar magnituds que varien de forma contínua, que poden tenir, a priori, qualsevol valor. Els valors d'aquestes magnituds es coneixen també d'una forma contínua en el temps.
Els senyals digitals, per altra banda, poden provenir d'ordinadors, de sistemes que llegeixen suports digitals (com ara un CD) o bé han estat convertits per un conversor analògic-digital. Aquests senyals es caracteritzen per ésser representats per mitjà d'una certa quantitat de nombres (dígits). Així, els valors que poden prendre les magnituds representades digitalment són sempre graons d'una certa escala. Per altra banda, els valors digitals no es coneixen de manera contínua en el temps, sinó que se'n prenen mostres amb una certa freqüència, o quan esdevé alguna circumstància d'interès.
Tipus de processament de senyals analògics
[modifica]Processament analògic del senyal
[modifica]Els senyals analògics poden ser tractats mitjançant circuits electrònics analògics.
Processament digital del senyal
[modifica]No obstant la simplicitat del tractament analògic, la tendència actual és cap a la digitalització del senyal i el seu posterior tractament digital mitjançant ordinadors o altres sistemes basats en microprocessadors. D'entre els basats en microprocessadors, n'hi ha un tipus anomenat processador digital del senyal (DSP) especialment pensat per a aquesta mena d'operacions.
Processament estadístic del senyal
[modifica]El processament estadístic del senyal és un enfocament que tracta els senyals com a processos estocàstics, utilitzant les seves propietats estadístiques per realitzar tasques de processament de senyal.[7] Les tècniques estadístiques s'utilitzen àmpliament en aplicacions de processament de senyals. Per exemple, es pot modelar la distribució de probabilitat del soroll produït en fotografiar una imatge, i construir tècniques basades en aquest model per reduir el soroll a la imatge resultant.
Processament no lineal del senyal
[modifica]El processament no lineal del senyal implica l'anàlisi i el processament de senyals produïts a partir de sistemes no lineals i poden ser en els dominis de temps, freqüència o espaciotemporal.[8][9] Els sistemes no lineals poden produir comportaments molt complexos, incloses les bifurcacions, caos, harmònica, i subharmònica que no es poden produir ni analitzar mitjançant mètodes lineals.
El processament de senyal polinomial és un tipus de processament de senyal no lineal, on els sistemes polinòmics es poden interpretar com a extensions conceptualment directes de sistemes lineals en cas no lineal.[10]
Mètodes matemàtics aplicats
[modifica]- Equacions diferencials [11]
- Relació de recurrència [12]
- Teoria de les transformacions
- Anàlisi temps-freqüència – per processar senyals no estacionaris [13]
- Estimació espectral – per determinar el contingut espectral (és a dir, la distribució de la potència sobre la freqüència) d'una sèrie temporal[14]
- Processament estadístic del senyal – analitzar i extreure informació de senyals i sorolls a partir de les seves propietats estocàstiques
- Teoria lineal de sistemes invariants en el temps i teoria de transformades
- Processament de senyals polinòmics – anàlisi de sistemes que relacionen entrada i sortida mitjançant polinomis
- Identificació del sistema i classificació [8]
- Càlcul
- Anàlisi complexa [15]
- Espais vectorials i àlgebra lineal [16]
- Anàlisi funcional [17]
- Probabilitat i processos estocàstics [7]
- Teoria de la detecció
- Teoria de l'estimació
- Optimització [18]
- Mètodes numèrics
- Sèries temporals
- Mineria de dades – per a l'anàlisi estadística de relacions entre grans quantitats de variables (en aquest context que representen molts senyals físics), per extreure patrons interessants desconeguts fins ara
Aplicacions
[modifica]- Processament de senyals d'àudio – per a senyals elèctrics que representen el so, com ara la parla o la música[19]
- Processament d'imatge – en càmeres digitals, ordinadors i diversos sistemes d’imatge
- Processament de vídeo – per interpretar imatges en moviment
- Comunicació sense fils – generacions de formes d'ona, demodulació, filtratge, igualació
- Sistemes de control
- Processament de matrius – per processar senyals a partir de matrius de sensors
- Procés de control – s'utilitzen diversos senyals, inclòs el bucle de corrent estàndard de la indústria de 4-20 mA
- Sismologia
- Processament de senyals financers – analitzar dades financeres mitjançant tècniques de processament de senyals, especialment amb finalitats de predicció.
- Extracció de funcions, com ara comprensió d’imatges i reconeixement de veu.
- Millora de la qualitat, com ara la reducció del soroll, la millora de la imatge i la cancel·lació del ressò.
- Codificació de fonts, inclosa la compressió d'àudio, la compressió d'imatges i la compressió de vídeo.
- Processament del senyal genòmic [20]
Referències
[modifica]- ↑ 1,0 1,1 Sengupta, Nandini; Sahidullah, Md; Saha, Goutam Computers in Biology and Medicine, 75, 1, 8-2016, pàg. 118–129. DOI: 10.1016/j.compbiomed.2016.05.013. PMID: 27286184.
- ↑ Alan V. Oppenheim and Ronald W. Schafer. Discrete-Time Signal Processing. Prentice Hall, 1989, p. 1. ISBN 0-13-216771-9.
- ↑ Vignolo Barchiesi, Juan «Procesamiento Digital de Señales». Ediciones Universitarias de Valparaíso, 2008. Arxivat de l'original el 2021-09-27 [Consulta: 1r setembre 2021].
- ↑ Oppenheim i 1975, 5.
- ↑ «A Mathematical Theory of Communication – CHM Revolution». Computer History. [Consulta: 13 maig 2019].
- ↑ 6,0 6,1 Fifty Years of Signal Processing: The IEEE Signal Processing Society and its Technologies, 1948–1998. The IEEE Signal Processing Society, 1998.
- ↑ 7,0 7,1 Scharf, Louis L. Statistical signal processing: detection, estimation, and time series analysis. Boston: Addison–Wesley, 1991. ISBN 0-201-19038-9. OCLC 61160161.
- ↑ 8,0 8,1 Billings, S. A.. Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains. Wiley, 2013. ISBN 978-1119943594.
- ↑ «A New Approach to Signal Processing of Spatiotemporal Data». A: 2018 IEEE Statistical Signal Processing Workshop (SSP). IEEE Xplore, 2018, p. 338–342. DOI 10.1109/SSP.2018.8450704. ISBN 978-1-5386-1571-3.
- ↑ V. John Mathews; Giovanni L. Sicuranza Polynomial Signal Processing. Wiley. ISBN 978-0-471-03414-8.
- ↑ Patrick Gaydecki. Foundations of Digital Signal Processing: Theory, Algorithms and Hardware Design. IET, 2004, p. 40–. ISBN 978-0-85296-431-6.
- ↑ Shlomo Engelberg. Digital Signal Processing: An Experimental Approach. Springer Science & Business Media, 8 gener 2008. ISBN 978-1-84800-119-0.
- ↑ Boashash, Boualem. Time frequency signal analysis and processing a comprehensive reference. Amsterdam: Elsevier, 2003. ISBN 0-08-044335-4.
- ↑ Stoica, 2005.
- ↑ Peter J. Schreier. Statistical Signal Processing of Complex-Valued Data: The Theory of Improper and Noncircular Signals. Cambridge University Press, 4 febrer 2010. ISBN 978-1-139-48762-7.
- ↑ Max A. Little. Machine Learning for Signal Processing: Data Science, Algorithms, and Computational Statistics. OUP Oxford, 13 agost 2019. ISBN 978-0-19-102431-3.
- ↑ Steven B. Damelin. The Mathematics of Signal Processing. Cambridge University Press, 2012. ISBN 978-1-107-01322-3.
- ↑ Daniel P. Palomar. Convex Optimization in Signal Processing and Communications. Cambridge University Press, 2010. ISBN 978-0-521-76222-9.
- ↑ Sarangi, Susanta; Sahidullah, Md; Saha, Goutam Digital Signal Processing, 104, 9-2020, pàg. 102795. arXiv: 2007.10729. DOI: 10.1016/j.dsp.2020.102795.
- ↑ Anastassiou, D. (en anglès) IEEE Signal Processing Magazine, 18, 4, 2001, pàg. 8–20. DOI: 10.1109/79.939833.
Bibliografia
[modifica]- P Stoica, R Moses. Spectral Analysis of Signals. NJ: Prentice Hall, 2005.
- Kay, Steven M. Fundamentals of Statistical Signal Processing. Upper Saddle River, New Jersey: Prentice Hall, 1993. ISBN 0-13-345711-7. OCLC 26504848.
- Papoulis, Athanasios. Probability, Random Variables, and Stochastic Processes. third. McGraw-Hill, 1991. ISBN 0-07-100870-5.
- Wong, Kainam Thomas. Statistical Signal Processing lecture notes at the University of Waterloo, Canada. (en anglès). Arxivat 2011-09-27 a Wayback Machine.
- Sayed, Ali H. Adaptive filters (en anglès). Hoboken, N.J.: Wiley-Interscience. ISBN 978-0-470-25388-5.
- Kailath, Thomas; Sayed, Ali H.; Ali H. Sayed; Hassibi, Babak; Babak Hassibi. Linear estimation (en anglès). Upper Saddle River, N.J.: Prentice Hall. ISBN 978-0-13-022464-4.
- Oppenheim, Alan V. Digital Signal Processing (en anglès). Prentice Hall, 1975. ISBN 0-13-214635-5.
- Stoica, Petre. Spectral Analysis of Signals (en anglès). NJ: Prentice Hall, 2005.
Vegeu també
[modifica]- Processament analògic de senyals
- Processament digital de senyals
- Senyal elèctric
- Electrònica analògica
- Electrònica
- Enginyeria elèctrica
- Condensador
- Inductor
- Resistència
- Transistor
- Circuit RC
- Circuit LC
- Circuit RLC
- Filtre passabanda
- Filtre de banda eliminada
- Filtre passaalt
- Filtre passabaix
- Circuit en sèrie
- Circuit en paral·lel