Buffonsches Nadelproblem

Das buffonsche Nadelproblem fragt nach der Wahrscheinlichkeit, dass eine willkürlich geworfene Nadel ein Gitter paralleler Linien schneidet. Es erlaubt unter anderem, die Kreiszahl ${\displaystyle \pi }$ experimentell zu bestimmen. Das Problem gehört zum Bereich der Integralgeometrie und war eines der ersten auf diesem Gebiet.^[1] Georges-Louis Leclerc de Buffon behandelte es erstmals 1733 vor der Pariser Akademie der Wissenschaften^[2] und nochmals ausführlicher im Supplement zu seiner Histoire Naturelle 1777.^[3][4]

Experimentelle Durchführung[Bearbeiten | Quelltext bearbeiten]

Benötigt werden möglichst viele identische Stäbchen. Auf einer ebenen Unterlage werden parallele Hilfslinien im Abstand ${\displaystyle d}$ konstruiert.

Alle vorhandenen Stäbchen werden zufällig auf der Unterlage verstreut. Abschließend zählt man, wie viele Stäbchen eine der Linien kreuzen.

Falls der Abstand ${\displaystyle d}$ der Linien gleich der Länge ${\displaystyle l}$ der Stäbchen ist, so erhält man eine Näherung für ${\displaystyle \pi }$, indem man die Anzahl aller genutzten Stäbchen mit 2 multipliziert und durch die Anzahl der Stäbchen, die eine Linie kreuzen, teilt.

Auf dem Bild rechts kreuzen 11 von 17 Stäbchen eine Linie; es ergibt sich also die Näherung

${\displaystyle {\hat {\pi }}={\frac {2\cdot 17}{11}}\approx 3{,}1}$.

Gilt ${\displaystyle d\geq l}$ (Fall kurzer Stäbchen), so ist (wie im Folgeabschnitt abgeleitet) die Formel für die Trefferwahrscheinlichkeit ${\displaystyle p={\tfrac {2\;\!\cdot \;\!l}{\pi \;\!\cdot \;\!d}}}$. Nach ${\displaystyle \pi }$ umgestellt, und unter Benutzung der relativen Häufigkeiten ${\displaystyle {\hat {p}}=N_{C}/N_{A}}$ als Schätzer für ${\displaystyle p}$ folgt der Schätzer

${\displaystyle {\hat {\pi }}={\frac {2\cdot N_{\!A}\cdot l}{N_{\;\!\!C}\cdot d}},}$

wobei ${\displaystyle N_{A}}$ die Anzahl aller Stäbchen der Länge ${\displaystyle l}$ bezeichnet. ${\displaystyle N_{C}}$ ist die Anzahl aller Stäbe, die eine der Linien kreuzen und ${\displaystyle d}$ ist der Abstand zweier benachbarter Linien.

Nach dem Gesetz der großen Zahlen nähert sich die relative Häufigkeit ${\displaystyle {\hat {p}}}$ für eine große Anzahl an Stäbchen der angegebenen Wahrscheinlichkeit an:

${\displaystyle {\tfrac {N_{\;\!\!C}}{N_{\!A}}}\rightarrow p}$  und damit  ${\displaystyle {\tfrac {2\;\!\cdot \;\!N_{\!A}\;\!\cdot \;\!l}{N_{\;\!\!C}\;\!\cdot \;\!d}}\rightarrow \pi }$  für  ${\displaystyle N_{\!A}\rightarrow \infty }$.

Für den Fall ${\displaystyle d<l\ }$ (Fall langer Stäbchen) ist der Zusammenhang etwas komplizierter.^[5]

Beweis für Nadeln beliebiger Länge[Bearbeiten | Quelltext bearbeiten]

Der Winkel ${\displaystyle \Phi }$, unter dem die Nadel auf die Linien trifft, ist eine gleichverteilte Zufallsvariable. Eine Realisierung dieser Zufallsvariablen wird durch ein kleines ${\displaystyle \varphi }$ notiert. Ob eine Nadel eine Linie berührt (1) oder nicht (0), ist eine Bernoulli-verteilte Zufallszahl ${\displaystyle Z}$. Der Erwartungswert ${\displaystyle E[Z]=P(Z=1)}$ wird im Experiment geschätzt: ${\displaystyle {\hat {E}}[Z]={\frac {1}{N_{A}}}\sum _{i=1}^{N_{A}}z_{i}}$, wobei ${\displaystyle N_{A}}$ die Zahl der Würfe ist.

Fall kurzer Nadeln[Bearbeiten | Quelltext bearbeiten]

Für den Fall ${\displaystyle l\leq d}$ (kurze Nadel) betrachte man nur einen waagerechten Streifen der Breite ${\displaystyle d}$, siehe Abbildung rechts für den Fall ${\displaystyle l=d}$. Eine Nadel der Länge ${\displaystyle l}$ berührt den Rand, falls der auf der senkrechten gestrichelten Linie liegende Endpunkt der Nadel innerhalb eines Streifens der Breite ${\displaystyle l|{\cos {\varphi }}|}$ von einem der beiden Ränder liegt. Die Zufallsvariablen ${\displaystyle Z}$ und ${\displaystyle \Phi }$ besitzen eine gemeinsame Wahrscheinlichkeitsverteilung, da sie sich auf dasselbe Zufallsexperiment beziehen.^[6] Da die Zufallsvariablen ${\displaystyle Z}$ und ${\displaystyle \Phi }$ reellwertig sind, existiert eine reguläre bedingte Wahrscheinlichkeit von ${\displaystyle Z}$, gegeben ${\displaystyle \Phi }$.^[7] Daher gilt insbesondere

${\displaystyle p=P(Z=1)=\mathbb {E} [P(Z=1|\Phi )]=\int _{-\infty }^{\infty }P(Z=1|\Phi =\varphi )f_{\Phi }(\varphi )\mathrm {d} \varphi }$.^[8]

Mit der Wahrscheinlichkeit für die Existenz eines Schnittpunktes^[9]

${\displaystyle \lim _{\Delta \to 0}P(Z=1|\varphi -\Delta \leq \Phi \leq \varphi +\Delta )={\frac {l|{\cos {\varphi }}|}{d}}}$

im Fall ${\displaystyle \Phi =\varphi }$ und mit der Dichtefunktion

${\displaystyle f_{\Phi }(\varphi )={\begin{cases}{\frac {1}{2\pi }}&{\text{für }}0<\varphi <2\pi \\0&{\text{sonst}}\end{cases}}}$

der Zufallsvariablen ${\displaystyle \Phi }$ ergibt sich

${\displaystyle p=\int _{0}^{2\pi }{\frac {l\ |{\cos {\varphi }}|}{d}}{\frac {1}{2\pi }}\mathrm {d} \varphi ={\frac {2l}{\pi d}}\;.}$

Somit ist ${\displaystyle E[Z]=P(Z=1)={\frac {2l}{\pi d}}}$ bzw. ${\displaystyle \pi ={\frac {2l}{E[Z]d}}}$.

Daher ist ${\displaystyle {\hat {\pi }}={\frac {2l}{{\hat {E}}[Z]d}}}$ ein Schätzer für ${\displaystyle \pi }$, mit ${\displaystyle {\hat {E}}[Z]={\frac {1}{N_{A}}}\sum _{i=1}^{N_{A}}z_{i}}$. Asymptotisch für große Stichprobenumfänge ${\displaystyle N_{A}}$ ist ${\displaystyle {\hat {\pi }}}$ normalverteilt um den Mittelwert ${\displaystyle \pi }$, wobei die Varianz des Schätzers^[10] ${\displaystyle \operatorname {Var} [{\hat {\pi }}]={\frac {\pi ^{2}}{2N_{A}}}\left({\frac {\pi }{l/d}}-2\right)}$ ist.

Fall langer Nadeln[Bearbeiten | Quelltext bearbeiten]

Im Fall ${\displaystyle l>d}$ (lange Nadel) muss man die Möglichkeit der mehrfachen Berührung von Linien berücksichtigen, so dass die Formeln komplizierter werden:^[11]

${\displaystyle p={\frac {2}{\pi }}\left({\frac {l}{d}}+\operatorname {arcsec} {\frac {l}{d}}-{\sqrt {\left({\frac {l}{d}}\right)^{\!\!2}\!-1}}\right)}$

Man kann statt des Arkussekans in der letzten Formel auch ${\displaystyle \operatorname {arcsec} {x}=\arccos {\tfrac {1}{x}}={\tfrac {\pi }{2}}-\arcsin {\tfrac {1}{x}}}$ benutzen. Im Fall ${\displaystyle d=l}$ ergeben beide Formeln ${\displaystyle p={\tfrac {2}{\pi }}}$. Im Fall der langen Nadel wächst ${\displaystyle p}$ streng monoton mit der Nadellänge ${\displaystyle l}$ und geht für ${\displaystyle l\to \infty }$ gegen 1.

Der Beweis von Barbier für kleine Nadeln[Bearbeiten | Quelltext bearbeiten]

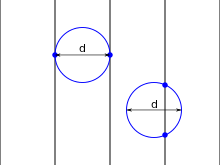
Barbier gab 1860^[12][13] für den Fall kleiner Nadeln einen Beweis, der ohne Integration auskommt. Zunächst wird gezeigt, dass der gesuchte Erwartungswert ${\displaystyle E}$ für die Anzahl der Treffer eine lineare Funktion der Länge der Nadel ist (${\displaystyle E=cl}$ mit der Länge ${\displaystyle l}$), was auch für beliebige Kurven gilt, da man sie durch einen Streckenzug approximieren kann. Zu bestimmen ist die Proportionalitätskonstante ${\displaystyle c}$. Dazu wird der Fall von Kreisen mit Durchmesser ${\displaystyle d}$ betrachtet, die immer genau 2 Treffer auf den Parallellinien im Abstand ${\displaystyle d}$ haben. Man nähert den Kreis durch ein- und umgeschriebene Vielecke ${\displaystyle P,Q}$ (mit dem Umfang ${\displaystyle p}$ bzw. ${\displaystyle q}$) und erhält

${\displaystyle E(P)=cp\leq 2\leq E(Q)=cq}$

sowie beim Grenzübergang der Seitenanzahl der Vielecke gegen Unendlich

${\displaystyle cd\pi \leq 2\leq cd\pi }$,

also ${\displaystyle c={\tfrac {2}{d\pi }}}$ und somit das gewünschte Ergebnis ${\displaystyle E={\tfrac {2l}{d\pi }}}$.

Wegen seiner Eleganz wurde der Beweis von Barbier von Aigner und Ziegler in Das Buch der Beweise aufgenommen.

Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]

Man kann nach anderen Figuren als Strecken fragen, die zufällig auf eine Ebene geworfen werden, beispielsweise Polygonzüge. Aus der Formel für das Buffonproblem folgt für Polygone mit einem Durchmesser kleiner ${\displaystyle d}$ und dem Umfang ${\displaystyle U}$ die Trefferwahrscheinlichkeit

${\displaystyle p={\frac {2U}{\pi d}}}$.

Nähert man eine geschlossene Kurve durch einen solchen Polygonzug,^[14] ergibt sich auch in diesem Fall die Trefferwahrscheinlichkeit, wenn man den Umfang ${\displaystyle U}$ des Polygonzugs durch die Länge der Kurve ersetzt (auch hier muss der Durchmesser kleiner ${\displaystyle d}$ sein). Das sind die Ausgangspunkte zu Methoden der Integralgeometrie, aus geeigneten Trefferwahrscheinlichkeiten Formeln zum Beispiel für die Bogenlänge von Kurven zu erhalten.

Im sogenannten Buffon-Laplace-Nadelproblem fragt man nach der Trefferwahrscheinlichkeit für ein Rechteck-Gitter mit Seitenlängen ${\displaystyle a}$ und ${\displaystyle b}$. Für kleine Nadeln (${\displaystyle l<a}$ und ${\displaystyle l<b}$) ergibt sich^[15]

${\displaystyle p={\frac {2l(a+b)-l^{2}}{\pi ab}}}$.

Das Problem lässt sich auch auf den Wurf anderer Körper ausdehnen, wie in dem auch von Buffon 1733 angesprochenen Franc-Carreau-Problem:^[16] Man werfe eine Münze (Kreisscheibe, Durchmesser ${\displaystyle l}$) auf ein Quadratgitter (Seitenlänge ${\displaystyle d}$), wobei ${\displaystyle l<d}$ sei. Wie groß ist die Wahrscheinlichkeit, dass die Münze auf dem Rand zu liegen kommt? Da die Münze den Rand nur berühren kann, falls ihr Mittelpunkt im Abstand ${\displaystyle {\tfrac {l}{2}}}$ vom Rand ist, lässt sich durch einfache geometrische Überlegungen die Trefferwahrscheinlichkeit als Flächenverhältnis angeben:

${\displaystyle p={\frac {d^{2}-{(d-l)}^{2}}{d^{2}}}={\frac {l}{d}}\left(2-{\frac {l}{d}}\right)}$

Für ein faires Spiel muss ${\displaystyle l=d\left(1-{\tfrac {1}{\sqrt {2}}}\right)\approx 0{,}293\cdot d}$ sein.

Historisches[Bearbeiten | Quelltext bearbeiten]

Über das Nadelproblem und ähnliche Probleme berichtete Buffon 1733 vor der Französischen Akademie der Wissenschaften, wie Fontenelle^[17] berichtet. Von Interesse war es in Zusammenhang mit einem damals bei Adligen beliebten Spiel: Man werfe eine Münze auf ein Kachelmuster und wette auf die Lage der Münze, ob sie eine der Ritzen berührt oder nicht (Franc-Carreau-Problem). Buffon ging darauf ausführlicher 1777 ein, wobei er im Fall des Nadelproblems auch schon die korrekte Antwort vermutete. Insbesondere leitete er aus der Formel für kurze Nadeln ab, dass für ein faires Wetten (d. h. für Wetten mit 50-prozentiger Gewinnwahrscheinlichkeit) beim Nadelproblem das Verhältnis ${\displaystyle {\tfrac {l}{d}}={\tfrac {\pi }{4}}}$ sein muss. Für den Wurf auf ein quadratisches Gitter gab er allerdings eine falsche Formel an. Die korrekte Formel (auch im Fall eines Rechteck-Gitters) gab erst Pierre Simon de Laplace 1812 an,^[18] ohne Buffon zu erwähnen. Er zitierte das als Beispiel für die Anwendung der Wahrscheinlichkeitstheorie auf die Bestimmung von Kurvenlängen und Flächeninhalten. Das wurde dann unter anderem von Isaac Todhunter 1865 ausgeführt. Aus der Beschäftigung mit dem buffonschen Nadelproblem ergab sich auch Croftons Formel (siehe Morgan Crofton) für die Bogenlänge einer Kurve in der Integralgeometrie (1868).

Der Italiener Mario Lazzarini soll 1901 den umfangreichsten experimentellen Test der Formel durchgeführt haben (mit einer eigens gebauten Maschine), mit 3408 Würfen von Nadeln mit einem Längenverhältnis ${\displaystyle {\tfrac {l}{d}}={\tfrac {5}{6}}}$. Sein Ergebnis war 1808 Treffer, so dass sich ein Wert für ${\displaystyle \pi }$ von ${\displaystyle 3{,}1415929\ldots }$ ergab, auf sechs Stellen hinter dem Komma genau. Die von ihm angegebenen Zahlen sind jedoch verdächtig (andere Autoren interpretierten das als Glückstreffer^[19][20]) und scheinen auf die bekannte Näherung ${\displaystyle {\tfrac {355}{113}}}$ für ${\displaystyle \pi }$ zugeschnitten zu sein.^[21][22] Der Astronom Rudolf Wolf^[23] führte das Experiment 1850 aus mit ${\displaystyle {\tfrac {l}{d}}=0{,}8}$ und erhielt bei 5000 Würfen 2532 Treffer, entsprechend einer Abschätzung für ${\displaystyle \pi }$ von ${\displaystyle 3{,}1596}$.^[24] Weitere Experimente führte Ambrose Smith 1855^[25] mit 3204 Würfen (${\displaystyle {\tfrac {l}{d}}=0{,}6}$) bei 1218 Treffern aus,^[26] was für ${\displaystyle \pi }$ einen Wert von ${\displaystyle 3{,}155\ldots }$ ergibt. Hans-J. Bentz führte das Experiment mit 2000 Würfen aus und erhielt ${\displaystyle 3{,}1430\ldots }$ für ${\displaystyle \pi }$.^[27][28]

Literatur[Bearbeiten | Quelltext bearbeiten]

• Martin Aigner, Günter M. Ziegler: Das Buch der Beweise, Springer Verlag 2002, Kapitel 24 Das Nadelproblem von Buffon, S. 179–182.
• Persi Diaconis: Buffon’s Needle Problem with a Long Needle, J. Appl. Prob. 13, 1976, S. 614–618 (Verteilung der Anzahl der Treffer bei langen Nadeln).
• P. Holgate: Buffon’s cycloid, Studies in the history of probability and statistics XXXIX, Biometrika 68 (3) (1981), 712–716 (zur Geschichte).
• Magdalena Hyksova, Anna Kalousova, Ivan Saxl: Early history of geometric probability and stereology, Image Anal. Stereology 31, 2012, 1–16, pdf.
• Maurice George Kendall, P. A. P. Moran: Geometric Probability, Charles Griffin, London 1963, S. 70 ff.
• P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, Buffonsches Nadelproblem (Buffon’s needle problem), S. 46–47. 
• Isaac Todhunter: A History of the mathematical theory of probability from the time of Pascal to that of Laplace, Macmillan 1865, S. 347 ff., Archive.
• L. Schroeder: Buffon’s needle problem: An exciting application of many mathematical concepts, Mathematics Teacher, 67, 1974, S. 183–186.
• James Victor Uspensky: Introduction to Mathematical Probability, McGraw Hill 1937, S. 112 ff.

Weblinks[Bearbeiten | Quelltext bearbeiten]

• Eric Weisstein: Buffon’s Needle Problem. In: MathWorld (englisch).
• Paul Kunkel Buffon’s Needle
• Buffon’s Needle Problem, Cut the Knot, Alex Bogomolny
• Buffon’s Needle Problem, Cut the Knot, Scott Brodie

Einzelnachweise und Anmerkungen[Bearbeiten | Quelltext bearbeiten]

1. ↑ Später stellte sich heraus, dass auch Isaac Newton Überlegungen auf diesem Gebiet angestellt hatte, diese aber nicht veröffentlichte.
2. ↑ Isaac Todhunter: History of the Mathematical Theory of Probability, 1865, S. 203.
3. ↑ John J. O’Connor, Edmund F. Robertson: Georges Louis Leclerc Comte de Buffon. In: MacTutor History of Mathematics archive (englisch).
4. ↑ Buffon: Essai d’arithmétique morale, Histoire naturelle, générale er particulière, Supplément 4, 46–123, 1777. Der Essay stammt aus der Zeit um 1760. Todhunter, History of the Mathematical Theory of Probability, 1865, S. 344.
5. ↑ Eric Weisstein: Buffon’s Needle Problem. In: MathWorld (englisch).
6. ↑ In mathematischer Sprechweise: ${\displaystyle Z}$ und ${\displaystyle \Phi }$ sind messbare Funktionen auf demselben Wahrscheinlichkeitsraum.
7. ↑ Die Existenz einer regulären bedingten Wahrscheinlichkeit, bei der die Bedingung die Wahrscheinlichkeit Null hat, ist nicht trivial, aber hier durch die spezielle Struktur der reellen Zahlen gewährleistet. In allgemeineren Messräumen kann diese Eigenschaft verlorengehen.
8. ↑ Hierbei ist ${\displaystyle P(Z=1|\Phi =\varphi )}$ keine elementare bedingte Wahrscheinlichkeit, insbesondere gilt nicht ${\displaystyle P(Z=1|\Phi =\varphi )={\frac {P(Z=1,\Phi =\varphi )}{P(\Phi =\varphi )}}}$, denn für die Wahrscheinlichkeit gilt ${\displaystyle P(\Phi =\varphi )=0}$, da ${\displaystyle \{\Phi =\varphi \}}$ eine Nullmenge beschreibt. Beachte, dass für die Wahrscheinlichkeitsdichte jedoch sehr wohl ${\displaystyle f_{\Phi }(\varphi )={\frac {1}{2\pi }}}$ für ${\displaystyle 0<\varphi <2\pi }$ gilt.
9. ↑ Zur bedingten Wahrscheinlichkeit als Grenzwert elementarer bedingter Wahrscheinlichkeiten siehe Michael A. Proschan, Pamela A. Shaw: Essentials of Probability Theory for Statisticians. CRC Press, Boca Raton 2016, ISBN 978-1-4987-0419-9, Abschnitt 10.8 Conditional Distribution Functions als Derivatives, S. 237–238. 
10. ↑ https://mathworld.wolfram.com/BuffonsNeedleProblem.html
11. ↑ Die Ableitung ist aber nicht viel schwieriger. Man macht beim Integrationsbereich eine Fallunterscheidung in einen Bereich, in dem nur eine Berührung stattfinden kann, bei dem die Integration wie bei kurzen Nadeln ausgeführt werden kann, und einen Bereich mit mindestens einer Berührung, dort ist die Wahrscheinlichkeit 1. Siehe Aigner, Ziegler.
12. ↑ E. Barbier: Note sur le problème de l’aiguelle et le jeu du joint couvert, J. Math. Pures et Appliqués, Band 5, 1860, S. 273–286.
13. ↑ Aigner, Ziegler: Das Buch der Beweise, Springer Verlag, Kapitel 24.
14. ↑ Zum Beispiel Boris Wladimirowitsch Gnedenko: Theory of Probability, MIR Publishers, 1978, S. 38 f.
15. ↑ Eric Weisstein: Buffon-Laplace Needle Problem. In: MathWorld (englisch).
16. ↑ Diderot, Enzyklopädie 1752 zum Franc Carreau Problem, PDF (Memento vom 21. September 2013 im Internet Archive)
17. ↑ Histoire de l’Academie royale des Sciences, année 1733, Paris 1735, S. 43–45, nur in einer kurzen Mitteilung.
18. ↑ Laplace: Théorie analytique des probabilités, Paris: Veuve Courcier, 1812, S. 359 ff.
19. ↑ Genauer zur Analyse von Resultaten wie dem von Lazzarini. B. Gnedenko: Theory of Probability, MIR 1978, S. 37 f. Ist die Anzahl der Würfe kleiner als 5000, folgt schon aus elementaren Überlegungen, dass schon bei Änderung der Trefferanzahl um 1 die vierte Dezimalstelle geändert wird. Nach Gnedenko ist die Wahrscheinlichkeit, gerade diesen Zahlenwert für ${\displaystyle \pi }$ im Fall des Experiments von Lazzarini zu erhalten, kleiner als drei Prozent.
20. ↑ Kendall, Moran: Geometric Probability, S. 70 führen scherzhafter Weise in ihrer Tabelle der Experimente auch folgenden Eintrag von N. T. Gridgeman (Geometric Probability and the Number Pi, Scripta Mathematica 25, 1960, 183–195): Anzahl der Würfe: 2, Treffer: 1, ${\displaystyle {\tfrac {l}{d}}=0{,}7857}$, ergibt die Näherung für ${\displaystyle \pi }$ von ${\displaystyle 3{,}143}$
21. ↑ Nach Aigner, Ziegler: ${\displaystyle 3408\cdot {\tfrac {5}{6}}=2840=8\cdot 355}$.
22. ↑ Siehe dazu auch Lee Badger: Lazzarini’s Lucky Approximation of π, Mathematics Magazine, Band 67, 1994, 83–91.
23. ↑ Biographie von Wolf in der ADB von Siegmund Günther.
24. ↑ Kendall, Moran: Geometric Probability, S. 70.
25. ↑ Augustus De Morgan berichtet darüber in A Budget of Paradoxes 1872, siehe Uspensky: Introduction to Mathematical Probability, 113.
26. ↑ Genauer 1213 bei 11 unklaren Fällen, von denen die Hälfte gewertet wurde.
27. ↑ H.-J. Bentz: Das Buffon-Nadelproblem (1777), Praxis der Mathematik, 22, 1980, Heft 6, S. 167–171.
28. ↑ Simulation mit einem Computerprogramm (Monte-Carlo-Verfahren): Hans-J. Bentz: Zur Simulation des Buffon Nadelproblems, Praxis der Mathematik, 24, 1982, Heft 5, S. 129–137.