Ellipse
 Van Wikipedia, de gratis encyclopedie
Van Wikipedia, de gratis encyclopedie


Die Mittelachse des Kegels ist so weit geneigt, dass sich die Ellipse in der Seitenansicht von rechts in wahrer Größe zeigt.

Ellipsen sind in der Geometrie spezielle geschlossene ovale Kurven. Sie zählen neben den Parabeln und den Hyperbeln zu den Kegelschnitten. Eine anschauliche Definition verwendet die Eigenschaft, dass die Summe der Abstände eines Ellipsenpunktes von zwei vorgegebenen Punkten, den Brennpunkten, für alle Punkte gleich ist. Sind die Brennpunkte identisch, erhält man einen Kreis.
Jede Ellipse lässt sich in einem geeigneten Koordinatensystem durch eine Gleichung
oder Parameterdarstellung
beschreiben. Hieran erkennt man, dass man eine Ellipse als einen an der x-Achse um und an der y-Achse um gestreckten Einheitskreis auffassen kann.
Die Ellipse (von altgriechisch ἔλλειψις élleipsis, deutsch ‚das Unterlassen, Ausbleiben, Zurückbleiben‘) wurde von Apollonios von Perge (etwa 262–190 v. Chr.)[1] eingeführt und benannt, die Bezeichnung bezieht sich auf die Exzentrizität .[2]
Ellipsen treten nicht nur als ebene Schnitte eines Kegels auf. Auch auf Zylindern, Ellipsoiden, Hyperboloiden und elliptischen Paraboloiden gibt es Ellipsen.
In der Natur treten Ellipsen in Form von ungestörten keplerschen Planetenbahnen um die Sonne auf. Auch beim Zeichnen von Schrägbildern werden häufig Ellipsen benötigt, da ein Kreis durch eine Parallelprojektion im Allgemeinen auf eine Ellipse abgebildet wird (siehe Ellipse (Darstellende Geometrie)).
Definition einer Ellipse als geometrischer Ort[Bearbeiten | Quelltext bearbeiten]




Es gibt verschiedene Möglichkeiten, Ellipsen zu definieren. Neben der üblichen Definition über gewisse Abstände von Punkten ist es auch möglich, eine Ellipse als Schnittkurve zwischen einer entsprechend geneigten Ebene und einem Kegel zu bezeichnen (siehe 1. Bild) oder als affines Bild des Einheitskreises.
Eine Ellipse ist der geometrische Ort aller Punkte der Ebene, für die die Summe der Abstände zu zwei gegebenen Punkten und gleich einer gegebenen Konstante ist. Diese Konstante wird üblicherweise mit bezeichnet. Die Punkte und heißen Brennpunkte:
Um eine Strecke auszuschließen, setzt man voraus, dass größer als der Abstand der Brennpunkte ist. Falls die beiden Brennpunkte zusammenfallen, ist ein Kreis mit Radius . Dieser einfache Fall wird in den folgenden Überlegungen oft stillschweigend ausgeschlossen, da die meisten Aussagen über Ellipsen im Kreisfall trivial werden.
Der Mittelpunkt der Strecke heißt Mittelpunkt der Ellipse. Die Gerade durch die Brennpunkte ist die Hauptachse und die dazu orthogonale Gerade durch die Nebenachse. Die beiden Ellipsenpunkte auf der Hauptachse sind die Hauptscheitel. Der Abstand der Hauptscheitel zum Mittelpunkt ist und heißt die große Halbachse. Die beiden Ellipsenpunkte auf der Nebenachse sind die Nebenscheitel, und ihr Abstand zum Mittelpunkt ist jeweils die kleine Halbachse . Den Abstand der Brennpunkte zum Mittelpunkt nennt man die lineare Exzentrizität und die numerische Exzentrizität. Mit dem Satz des Pythagoras gilt (siehe Zeichnung). Die Gleichung kann man auch so interpretieren: Wenn der Kreis um mit Radius ist, dann ist der Abstand des Punktes zum Kreis gleich dem Abstand des Punktes zum Brennpunkt :
heißt Leitkreis der Ellipse bzgl. des Brennpunktes . Diese Eigenschaft sollte man nicht verwechseln mit der Leitlinieneigenschaft einer Ellipse (s. unten).
Mit Hilfe Dandelinscher Kugeln beweist man:
- Jeder Schnitt eines Kegels mit einer Ebene, die die Kegelspitze nicht enthält, und deren Neigung kleiner als die der Mantellinien des Kegels ist, ist eine Ellipse.
Aufgrund der Leitkreis-Eigenschaft ist eine Ellipse die Äquidistanz-Kurve zu jedem ihrer Brennpunkte und dem Leitkreis mit dem anderen Brennpunkt als Mittelpunkt.
Ellipse in kartesischen Koordinaten[Bearbeiten | Quelltext bearbeiten]
Gleichung[Bearbeiten | Quelltext bearbeiten]
A. Führt man kartesische Koordinaten so ein, dass der Mittelpunkt der Ellipse im Ursprung liegt, die -Achse die Hauptachse ist, und
- die Brennpunkte die Punkte ,
- die Hauptscheitel sind,
so ergibt sich für einen beliebigen Punkt der Abstand zum Brennpunkt als und zum zweiten Brennpunkt . Also liegt der Punkt genau dann auf der Ellipse, wenn die folgende Bedingung erfüllt ist:
Nach Beseitigung der Wurzeln durch geeignetes Quadrieren und Verwenden der Beziehung (s. o.) erhält man die Gleichung
- oder nach aufgelöst
sind die Nebenscheitel. Aus der Beziehung erhält man die Gleichungen
- und
Daraus ergeben sich noch die Beziehungen
Ist , so ist und die Ellipse ein Kreis.
Ist , so ist , und man nennt die Ellipse eine gleichseitige Ellipse oder Ellipse schönster Form. Diese entsteht z. B., wenn man einen Drehzylinder mit einer gegen die Zylinderachse um 45° geneigten Ebene schneidet: Die Länge der kleinen Halbachse der Ellipse ist dabei gleich dem Radius des Zylinders.
B. Die Ellipse in A. lässt sich auch mithilfe einer Bilinearform als Lösungsmenge der Gleichung auffassen.[3] Hierbei werden die Vektoren und mit dem gleichen Punkt identifiziert. Bei Einführung kartesischer Koordinaten ist die Matrix , ein Zeilenvektor und ein Spaltenvektor.
C. Eine Ellipse mit dem Mittelpunkt im Ursprung und den Brennpunkten auf der -Achse heißt auch in 1. Hauptlage. Wenn hier die obige Ellipsengleichung erwähnt wird, wird immer angenommen, dass und damit die Ellipse in 1. Hauptlage ist, was im „realen Leben“ aber nicht sein muss. Da kann durchaus auch vorkommen, was bedeutet, dass die Ellipse sich in 2. Hauptlage befindet (die Brennpunkte liegen auf der -Achse).
Aufgrund der Definition einer Ellipse gilt:
- Eine Ellipse ist symmetrisch zu ihren Achsen und damit auch zu ihrem Mittelpunkt.
(Die Symmetrieeigenschaft lässt sich auch leicht an der hier abgeleiteten Gleichung einer Ellipse erkennen.)
Halbparameter[Bearbeiten | Quelltext bearbeiten]
Die halbe Länge einer Ellipsensehne, die durch einen Brennpunkt geht und zur Hauptachse senkrecht verläuft, nennt man den Halbparameter, manchmal auch nur Parameter oder auch semi-latus rectum (die Hälfte des latus rectum = ) der Ellipse. Mit Hilfe der Gleichung einer Ellipse rechnet man leicht nach, dass
gilt. Der Halbparameter hat noch die zusätzliche Bedeutung (s. unten): Der Krümmungsradius in den Hauptscheiteln ist .
Tangente[Bearbeiten | Quelltext bearbeiten]
A. Für den Hauptscheitel bzw. hat die Tangente die Gleichung bzw. . Die einfachste Weise, die Gleichung der Tangente in einem Ellipsenpunkt zu bestimmen, ist, die Gleichung der Ellipse implizit zu differenzieren. Hiermit ergibt sich für die Ableitung
und damit die Punkt-Steigungs-Form der Tangente im Punkt :
Berücksichtigt man , so erhält man als Gleichung der Tangente im Punkt :
Diese Form schließt auch die Tangenten durch die Hauptscheitel ein. Letzteres gilt auch für die Vektorform
- .
B. Die in A. eingeführte Tangentengleichung lässt sich auch ohne Differentialrechnung als Spezialfall einer Polarengleichung einführen (s. u. Herleitung der Lagebeziehungen von Pol und Polare, D.). Sie entspricht einer Normalenform mit dem Normalenvektor . Von diesem lässt sich ein dazu rechtwinkeliger Richtungsvektor von ablesen. Da nur bis auf einen Skalar eindeutig ist, hat er die Formen
- ;
dies liefert den Richtungsvektor der in A. angegebenen Vektorform und auch die Steigung der dort angegebenen Punktsteigungsform.
Eine zeichnerische Bestimmung von Ellipsentangenten findet man im Artikel Ellipse (Darstellende Geometrie).
Gleichung einer verschobenen Ellipse[Bearbeiten | Quelltext bearbeiten]
Verschiebt man die obige Ellipse so, dass der Mittelpunkt der Punkt ist, ergibt sich die Mittelpunktsform einer Ellipse, deren Achsen parallel zu den Koordinatenachsen sind:
Parameterdarstellungen[Bearbeiten | Quelltext bearbeiten]
- Standarddarstellung
Die übliche Parameterdarstellung einer Ellipse verwendet die Sinus- und Kosinus-Funktion. Wegen beschreibt
die Ellipse
Verschiedene Möglichkeiten, den Parameter geometrisch zu interpretieren, werden im Abschnitt Ellipsen zeichnen angegeben.
- Rationale Parameterdarstellung
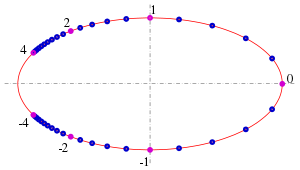
Mit der Substitution und trigonometrischen Formeln erhält man
und damit die rationale Parameterdarstellung einer Ellipse:
Die rationale Parameterdarstellung hat folgende Eigenschaften (s. Bild):
- Für wird der positive Hauptscheitel dargestellt: ; für der positive Nebenscheitel: .
- Übergang zur Gegenzahl des Parameters spiegelt den dargestellten Punkt an der -Achse: .
- Übergang zum Kehrwert des Parameters spiegelt den dargestellten Punkt an der -Achse: .
- Der negative Hauptscheitel kann mit keinem reellen Parameter dargestellt werden. Die Koordinaten desselben sind die Grenzwerte der Parameterdarstellung für unendliches positives oder negatives : .
Rationale Parameterdarstellungen der Kegelschnitte (Ellipse, Hyperbel, Parabel) spielen im CAD-Bereich bei quadratischen rationalen Bezierkurven eine wichtige Rolle.[4]
- Tangentensteigung als Parameter
Eine Parameterdarstellung, die die Tangentensteigung in dem jeweiligen Ellipsenpunkt verwendet, erhält man durch Differentiation der Parameterdarstellung :
Mit Hilfe trigonometrischer Formeln ergibt sich
Ersetzt man in der Standarddarstellung und , erhält man schließlich
Dabei ist die Tangentensteigung im jeweiligen Ellipsenpunkt, die obere und die untere Hälfte der Ellipse. Die Punkte mit senkrechten Tangenten (Scheitel ) werden durch diese Parameterdarstellung nicht erfasst.
Die Gleichung der Tangente im Punkt hat die Form . Der -Abschnitt ergibt sich durch Einsetzen der Koordinaten des zugehörigen Ellipsenpunktes :
Diese Hauptform der Tangentengleichung ist ein wesentliches Hilfsmittel bei der Bestimmung der orthoptischen Kurve einer Ellipse.
Bemerkung: Die Hauptform der Tangentengleichung und die Koordinaten von lassen sich auch ohne Differentialrechnung und ohne trigonometrische Formeln herleiten, indem die Tangente als Spezialfall einer Polare aufgefasst wird (s. u. Herleitung der Lagebeziehungen von Pol und Polare, D.)
- Verschobene Ellipse
Eine verschobene Ellipse mit Mittelpunkt wird durch
beschrieben.
Eine Parameterdarstellung einer beliebigen Ellipse ist in dem Abschnitt Ellipse als affines Bild des Einheitskreises enthalten.
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Brennpunkteigenschaft[Bearbeiten | Quelltext bearbeiten]

Die Verbindungslinie zwischen einem Brennpunkt und einem Punkt der Ellipse heißt Brennlinie, Leitstrahl oder Brennstrahl. Ihren Namen erhielten Brennpunkte und Brennstrahlen aufgrund der folgenden Eigenschaft:
- Der Winkel zwischen den beiden Brennstrahlen in einem Punkt der Ellipse wird durch die Normale in diesem Punkt halbiert.
- Anwendungen
- Der Einfallswinkel, den der eine Brennstrahl mit der Tangente bildet, ist gleich dem Ausfallswinkel, den die Tangente mit dem anderen Brennstrahl bildet. Ein Lichtstrahl, der von einem Brennpunkt ausgeht, wird demnach an der Ellipsentangente so reflektiert, dass er den anderen Brennpunkt trifft. Bei einem ellipsenförmigen Spiegel treffen sich demnach alle von einem Brennpunkt ausgehenden Lichtstrahlen in dem anderen Brennpunkt.
- Da alle Wege von einem zum anderen Brennpunkt (entlang zusammengehöriger Brennstrahlen) gleich lang sind, wird z. B. Schall durch konstruktive Interferenz „verstärkt“ übertragen.
- Die Tangente im Ellipsenpunkt ist die Winkelhalbierende des Außenwinkels. Da Winkelhalbierenden leicht zu konstruieren sind, bietet die Brennpunkteigenschaft eine einfache Methode, die Tangente in einem Ellipsenpunkt zu konstruieren (Eine weitere Tangentenkonstruktion wird in Ellipse (Darstellende Geometrie) beschrieben.).
Zwei Ellipsen mit denselben Brennpunkten nennt man konfokal. Durch jeden Punkt, der nicht zwischen den Brennpunkten liegt, gibt es genau eine Ellipse mit den Brennpunkten . Zwei konfokale Ellipsen haben keinen Schnittpunkt (s. Definition einer Ellipse).
Beweis der Brennpunkteigenschaft
Da die Tangente senkrecht zur Normalen verläuft, ist die obige Behauptung bewiesen, wenn die analoge Aussage für die Tangente gilt:
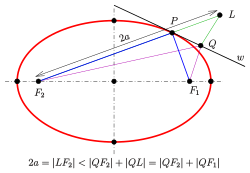
- Der Außenwinkel der Brennstrahlen in einem Ellipsenpunkt wird von der Tangente in diesem Punkt halbiert (s. Bild).
Es sei der Punkt auf der Geraden mit dem Abstand zum Brennpunkt ( ist die große Halbachse der Ellipse). Die Gerade sei die Winkelhalbierende der Außenwinkel der Brennstrahlen . Um nachzuweisen, dass die Tangente ist, zeigt man, dass auf kein weiterer Ellipsenpunkt liegen kann. Anhand der Zeichnung und der Dreiecksungleichung erkennt man, dass
gilt. Dies bedeutet, dass ist. Wenn ein Punkt der Ellipse wäre, müsste die Summe aber gleich sein.
Bemerkung: Ein Beweis mit Mitteln der analytischen Geometrie befindet sich im Beweisarchiv.[5]
Natürliches Vorkommen und Anwendung in der Technik:
Die Decken mancher Höhlen ähneln einer Ellipsenhälfte. Befindet man sich – mit den Ohren – in einem Brennpunkt dieser Ellipse, hört man jedes Geräusch, dessen Ursprung im zweiten Brennpunkt liegt, verstärkt („Flüstergewölbe“). Diese Art der Schallübertragung funktioniert in einigen Stationen der Pariser Métro sogar von Bahnsteig zu Bahnsteig. Das gleiche Prinzip der Schallfokussierung wird heute zur Zertrümmerung von Nierensteinen mit Stoßwellen verwendet. Auch im lampengepumpten Nd:YAG-Laser wird ein Reflektor in Form einer Ellipse verwendet. Die Pumpquelle – entweder eine Blitzlampe oder eine Bogenlampe – wird in dem einen Brennpunkt positioniert, und der dotierte Kristall wird in den anderen Brennpunkt gelegt.
Direktrix[Bearbeiten | Quelltext bearbeiten]

Für eine echte Ellipse, d. h. , bezeichnet man eine Parallele zur Nebenachse im Abstand als Direktrix oder Leitlinie. Für einen beliebigen Punkt der Ellipse ist das Verhältnis seines Abstands von einem Brennpunkt zu dem Abstand von der Direktrix auf der entsprechenden Seite der Nebenachse gleich der numerischen Exzentrizität:
- Es ist
Beweis:
Mit sowie und den binomischen Formeln ist
- .
Die Umkehrung dieser Aussage gilt auch und kann zu einer weiteren Definition einer Ellipse benutzt werden (ähnlich wie bei einer Parabel):
- Für einen Punkt (Brennpunkt), eine Gerade (Leitlinie) nicht durch und eine reelle Zahl mit ist die Menge der Punkte (geometrischer Ort), für die der Quotient der Abstände zu dem Punkt und der Geraden gleich ist, eine Ellipse:
Die Wahl , also die Exzentrizität eines Kreises, ist in diesem Zusammenhang nicht erlaubt. Man kann als Leitlinie eines Kreises die unendlich entfernte Gerade auffassen.

Beweis:
Es sei und ein Punkt der Kurve. Die Leitlinie hat die Gleichung . Mit und der Beziehung ergibt sich
- und
Die Substitution liefert
Dies ist die Gleichung einer Ellipse () oder einer Parabel () oder einer Hyperbel (). All diese nicht-ausgearteten Kegelschnitte haben den Ursprung als Scheitel gemeinsam (s. Bild).
Für führt man neue Parameter und ein; die obige Gleichung wird dann zu
was die Gleichung einer Ellipse mit Mittelpunkt , der -Achse als Hauptachse und den Halbachsen ist.
Allgemeiner Fall:
Für den Brennpunkt und die Leitlinie erhält man die Gleichung
Die rechte Seite der Gleichung benutzt die Hessesche Normalform einer Geraden, um den Abstand eines Punktes von einer Geraden zu berechnen.

Konstruktion der Leitlinie:
Wegen sind der Punkt der Leitlinie (siehe Bild) und der Brennpunkt bezüglich der Spiegelung am großen Scheitelkreis (im Bild grün) invers. Damit kann wie im Bild gezeigt aus mit Hilfe des großen Scheitelkreises konstruiert werden. Eine weitere Begründung für die Konstruktion liefert die Tatsache, dass der Brennpunkt und die Leitlinie sowohl bezüglich der Ellipse als auch bezüglich des großen Scheitelkreises ein Pol-Polare-Paar (siehe unten) bilden.
Konjugierte Durchmesser[Bearbeiten | Quelltext bearbeiten]

- Betrachtet man zu einem beliebigen Ellipsendurchmesser (einer Ellipsensehne durch den Ellipsenmittelpunkt) alle parallelen Sehnen, so liegen deren Mittelpunkte ebenfalls auf einem Ellipsendurchmesser . Man nennt den zu konjugierten Durchmesser.[6]
- Bildet man zum konjugierten Durchmesser erneut den konjugierten Durchmesser, so erhält man wieder den ursprünglichen. In der Zeichnung stimmt also der zu konjugierte Durchmesser mit dem ursprünglichen Durchmesser überein.
- Die Tangenten in den Endpunkten eines Durchmessers (etwa ) sind parallel zum konjugierten Durchmesser (im Beispiel ).
- Haupt- und Nebenachse sind das einzige Paar orthogonaler konjugierter Durchmesser.
- Ist die Ellipse ein Kreis, so sind genau die orthogonalen Durchmesser (auch) konjugiert.
- Sind konjugierte Durchmesser nicht orthogonal, so ist das Produkt ihrer Steigungen .
- Seien , konjugierte Durchmesser. Dann ist . (Satz des Apollonius)
- Für die Ellipse mit der Gleichung und der Parameterdarstellung gilt:
- ( Vorzeichen: (+,+) oder (−,−) )
- ( Vorzeichen: (−,+) oder (+,−) )
- liegen auf konjugierten Durchmessern und es ist
- Im Fall eines Kreises gilt
Konjugierte Durchmesser (erstrangig von Ellipsen) werden auch auf einer eigenen Wikipedia-Seite behandelt, ebenso der Satz des Apollonius (samt Beweis). Ein analytischer Gesamt-Beweis sämtlicher hier aufgeführter Aussagen, der von der gemeinsamen Bilinearform zweier Ursprungsgeraden ausgeht, findet sich im Beweisarchiv. Dieser Beweis benötigt weder trigonometrische Funktionen noch Parameterdarstellungen noch eine affine Abbildung.[7]
Eine Anwendungsmöglichkeit im Bereich des technischen Zeichnens besteht in der Möglichkeit, den höchsten Punkt einer Ellipse oder eines Ellipsenbogens beliebiger Lage über einer Linie zu finden – nützlich z. B. für korrekte 2D-Darstellungen nicht-orthogonaler Ansichten zylindrischer Körper oder abgerundeter Kanten ohne Verwendung von 3D-Programmen. Wichtig ist dies für den sauberen Anschluss tangential von der Ellipse weg laufender Linien. Hierzu sind in die Ellipse oder den Ellipsenbogen zwei Sehnen parallel zur gewünschten Tangentenrichtung und die durch die Mittelpunkte der beiden Sehnen definierte Linie des zugehörigen konjugierten Durchmessers einzuzeichnen. Der Schnittpunkt dieser Linie mit der Ellipse oder dem Ellipsenbogen definiert den Anschlusspunkt der Tangente (und normalerweise den Endpunkt des Ellipsenbogens).
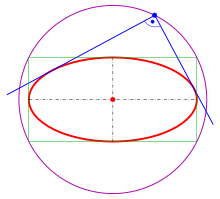
Orthogonale Tangenten[Bearbeiten | Quelltext bearbeiten]
Für die Ellipse liegen die Schnittpunkte orthogonaler Tangenten auf dem Kreis .
Diesen Kreis nennt man die orthoptische Kurve der gegebenen Ellipse, es ist der Umkreis des Rechtecks, das die Ellipse umschreibt.
Pol-Polare-Beziehung[Bearbeiten | Quelltext bearbeiten]
Führt man kartesische Koordinaten so ein, dass der Mittelpunkt der Ellipse im Ursprung liegt, so kann eine beliebige Ellipse mit der Gleichung beschrieben werden (s. o. Abschnitt Gleichung). Weiter ordnet für eine vorgegebene Ellipse eine Funktion je einem Punkt die Gerade zu. Bezüglich heißt Pol, die zugeordnete Gerade Polare. ist eine Bijektion; die inverse Funktion bildet je eine Polare auf einen Pol ab. Der Ellipsenmittelpunkt ist in keiner so definierten Polare enthalten, entsprechend existiert zu keine Polare. Die angegebene Gleichung der Polare lässt sich als Normalenform mit dem zugehörigen Normalenvektor auffassen.
Eine solche Beziehung zwischen Punkten und Geraden, die durch einen Kegelschnitt vermittelt wird, nennt man Pol-Polare-Beziehung oder einfach Polarität. Pol-Polare-Beziehungen gibt es auch für Hyperbeln und Parabeln, siehe auch Pol und Polare.
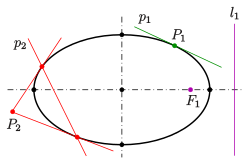
Zu Pol und Polare gelten folgende Lagebeziehungen:
- Der Brennpunkt und die Leitlinie sind polar zueinander. Da beide auch polar bezüglich des Scheitelkreises sind, lässt sich die Leitlinie auch mit Hilfe von Zirkel und Lineal konstruieren (siehe hierzu auch Kreisspiegelung). (1)
- Genau dann, wenn der Pol außerhalb der Ellipse liegt, hat die Polare zwei Punkte mit der Ellipse gemeinsam (s. Bild: ). (2)
- Genau dann, wenn der Pol auf der Ellipse liegt, hat die Polare genau einen Punkt mit der Ellipse gemeinsam (= die Polare ist eine Tangente; s. Bild: ). (3)
- Genau dann, wenn der Pol innerhalb der Ellipse liegt, hat die Polare keinen Punkt mit der Ellipse gemeinsam (s. Bild: ). (4)
- Jeder gemeinsame Punkt einer Polare und einer Ellipse ist Berührpunkt einer Tangente vom zugehörigen Pol an die Ellipse (s. Bild: ). (5)
- Der Schnittpunkt zweier Polaren ist der Pol der Geraden durch die Pole. (6)
Herleitung der Lagebeziehungen von Pol und Polare; alternative Herleitung einer Tangenten- und einer Ellipsengleichung[Bearbeiten | Quelltext bearbeiten]
A. Ist eine Polare parallel zur -Achse, so hat sie auch die Form . Mit dem zugehörigen Normalenvektor ist der zugehörige Pol Insbesondere folgt für die Polarität (1) von Brennpunkt und Direktrix.
Einsetzen der betrachteten Polare in die Mittelpunktform einer Ellipse ergibt für die Ordinate eines beliebigen Schnittpunkts die Bedingung ; die Diskriminante dieser quadratischen Gleichung in hat bis auf einen positiven Faktor die Form
- .
B. Ist eine Polare nicht parallel zur -Achse, so hat sie die Hauptform . Wegen lässt sich diese in die Normalenform umformen. Vergleich mit der Normalenform ergibt als Darstellung Koordinaten des Pols mit den Parametern der Hauptform:
- .
Einsetzen der Hauptform in die Mittelpunktform einer Ellipse ergibt für die Abszisse eines beliebigen Schnittpunkts die Bedingung ; die Diskriminante dieser quadratischen Gleichung in hat bis auf einen positiven Faktor die Form
C. Insgesamt erlaubt der Term bzw. für eine beliebige Polare folgende Unterscheidung paarweise disjunkter Fälle:
- Für hat die Polare mit der Ellipse keinen Punkt gemeinsam, und der Pol liegt innerhalb der Ellipse. Hieraus folgt (2).
- Für hat die Polare mit der Ellipse genau einen Punkt gemeinsam, und der Pol liegt auf der Ellipse. Also ist die Polare eine Tangente an die Ellipse, der Pol ihr Berührpunkt (s. Bild: ). Hieraus folgt (3).
- Für hat die Polare mit der Ellipse zwei Punkte gemeinsam, und der Pol liegt außerhalb der Ellipse. Hieraus folgt (4).
D. Ist eine Tangente nicht senkrecht, so ergibt Auflösung der Gleichung nach und Einsetzen von die Hauptform der Tangente:
;
Einsetzen von in die Koordinaten des Berührpunkts ergibt die Koordinaten der Parameterdarstellung einer Ellipse mit der Steigung als Parameter: ;
diese Parameterdarstellung erfasst die Hauptscheitel nicht.
E. Ausgehend von der im Abschnitt „Gleichung“, B. aufgeführten Bilinearform der Ellipse hat die Polare zum Punkt die Normalenformen
- mit dem Normalenvektor und
- mit dem Normalenvektor .
Ist ein Punkt der Ellipse, so beschreiben auch diese Gleichungen eine Tangente.
Diese koordinatenfreie rechnerische Darstellung der Polare eignet sich für Beweise. Mit den Koordinatendarstellungen und sowie den im Abschnitt „Gleichung“ angegebenen Matrizenkoordinaten für entsteht durch Auswertung der Matrizenprodukte wieder die im Abschnitt Pol-Polare-Beziehung angegebene Gleichung .
Beweis von (5) („Jeder gemeinsame Punkt einer Polare und einer Ellipse ist Berührpunkt einer Tangente vom zugehörigen Pol an die Ellipse.“):
Da die Ellipsenpunkte auf der Polare zu liegen, gilt und . Fasst man in diesen Gleichungen nicht , sondern bzw. als Normalenvektor auf, so besagen sie, dass die Tangenten in den Ellipsenpunkten den Punkt gemeinsam haben.
Beweis von (6) („Der Schnittpunkt zweier Polaren ist der Pol der Gerade durch die Pole.“):
Für einen Schnittpunkt zweier Polaren zu und gilt und . Fasst man in diesen Gleichungen nicht bzw. , sondern als Normalenvektor auf, so besagen sie, dass auf der Polare zu die Punkte , liegen. Weiter zeigt die Betrachtung der Parameterform mit
die punktweise Gleichheit der Gerade mit der Polare zu .
Ellipse als affines Bild des Einheitskreises[Bearbeiten | Quelltext bearbeiten]
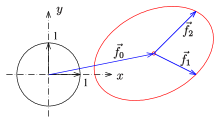
Eine andere Definition der Ellipse benutzt eine spezielle geometrische Abbildung, nämlich die Affinität. Hier ist die Ellipse als affines Bild des Einheitskreises definiert.[8]
Parameterdarstellung[Bearbeiten | Quelltext bearbeiten]
Eine affine Abbildung in der reellen Ebene hat die Form , wobei eine reguläre Matrix (Determinante nicht 0) und ein beliebiger Vektor ist. Sind die Spaltenvektoren der Matrix , so wird der Einheitskreis auf die Ellipse
abgebildet. ist der Mittelpunkt und sind zwei konjugierte Halbmesser (s. u.) der Ellipse. stehen i. A. nicht senkrecht aufeinander. D. h., und sind i. A. nicht die Scheitel der Ellipse. Diese Definition einer Ellipse liefert eine einfache Parameterdarstellung (s. u.) einer beliebigen Ellipse.
- Scheitel, Scheitelform
Da in einem Scheitel die Tangente zum zugehörigen Ellipsendurchmesser senkrecht steht und die Tangentenrichtung in einem Ellipsenpunkt ist, ergibt sich der Parameter eines Scheitels aus der Gleichung
und damit aus .
(Es wurden die Formeln benutzt.)
Falls ist, ist und die Parameterdarstellung schon in Scheitelform.
Die 4 Scheitel der Ellipse sind
Die Scheitelform der Parameterdarstellung der Ellipse ist
- Halbachsen
Mit den Abkürzungen folgt aus den beiden Sätzen von Apollonios:
Löst man nach auf, ergibt sich (s. Steiner-Ellipse)
- Flächeninhalt
Aus dem zweiten Satz von Apollonios folgt:
Der Flächeninhalt einer Ellipse ist
Für Beispiel 3 ist
- Beispiele
- liefert die übliche Parameterdarstellung der Ellipse mit der Gleichung .

Folge von Ellipsen: rotiert und so skaliert, dass zwei aufeinanderfolgende Ellipsen sich berühren - liefert die Parameterdarstellung der Ellipse, die aus durch Drehung um den Winkel und anschließende Verschiebung um hervorgeht. Die Parameterdarstellung ist schon in Scheitelform. D. h., und sind die Scheitel der Ellipse.

Transformation auf Scheitelform (Beispiel 3) - Die Parameterdarstellung
- einer Ellipse ist nicht in Scheitelform.
- Der Scheitelparameter ergibt sich aus zu .
- Die Scheitelform der Parameterdarstellung ist:
- Die Scheitel sind: und
- die Halbachsen:
Implizite Darstellung[Bearbeiten | Quelltext bearbeiten]
Löst man die Parameterdarstellung mit Hilfe der Cramerschen Regel nach auf und verwendet , erhält man die implizite Darstellung
- .
Für Beispiel 3 ergibt sich:
Dreht man die Ellipse mit der Gleichung um den Nullpunkt (Mittelpunkt), hat ihre Gleichung die Form
- wobei ist.
Liegt umgekehrt die Gleichung einer gedrehten Ellipse vor und man möchte die Vorteile der hier beschriebenen Parameterdarstellung nutzen, bestimmt man die Ortsvektoren zweier konjugierter Punkte. Wählt man als ersten Punkt , ergibt sich:
Beispiel: Für die Ellipse mit der Gleichung sind
die Ortsvektoren zweier konjugierter Punkte.
Ellipse im Raum[Bearbeiten | Quelltext bearbeiten]
Sind die Vektoren aus dem , so erhält man eine Parameterdarstellung einer Ellipse im Raum.
Peripheriewinkelsatz und 3-Punkteform für Ellipsen[Bearbeiten | Quelltext bearbeiten]
Kreise[Bearbeiten | Quelltext bearbeiten]
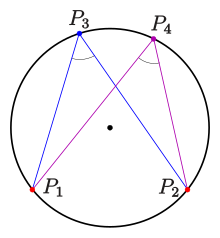
Ein Kreis mit der Gleichung ist durch drei Punkte




































































































































































































































































