Árbol de Pitágoras

El árbol de Pitágoras es un plano fractal construido a partir de cuadrados, inventado por el profesor Albert E. Bosman en 1942. Lleva el nombre del matemático griego Pitágoras debido a que en cada unión de 3 cuadrados se forma un triángulo rectángulo en una configuración utilizada tradicionalmente para representar el teorema de Pitágoras. Si el cuadrado más grande tiene un tamaño de L x L, todo el árbol de Pitágoras encajará perfectamente dentro de una caja de tamaño 6L × 4L.^[1]​^[2]​ Los detalles más finos de los árboles se asemejan a la curva de Lévy C.

construcción del árbol de Pitágoras comienza con un cuadrado. Sobre este cuadrado se construyen otros dos cuadrados, cada uno reducido por un factor lineal de ½√2 de tal manera que las esquinas de los cuadrados coinciden dos a dos. Este mismo procedimiento se aplica de forma recursiva para las dos cuadrados más pequeños, repitiéndose el proceso indefinidamente. La siguiente imagen muestra las primeras iteraciones en el proceso de construcción.[1]​[2]​ 

Orden 0	Orden 1	Orden 2	Orden 3

El límite de esta sucesión de conjuntos existe^[3]​ y es el fractal llamado árbol de Pitágoras.

La iteración n en la construcción suma 2ⁿ cuadrados de tamaño (½√2)ⁿ para un área total de 1. Así el área del árbol puede parecer que crece sin límite cuando n→∞. Sin embargo, algunos de los cuadrados se superponen a partir de la orden de iteración 5, el árbol en realidad tiene un área finita, ya que queda inscrito dentro de una caja de 6 x 4.^[1]​

Se puede demostrar fácilmente que el área A del árbol de Pitágoras debe estar en el rango de 5 <A < 18, que puede ser precisado con cálculos adicionales. Poco se sabe acerca el valor real de A.

• El número total de cuadrados en el paso ${\displaystyle n}$ es ${\displaystyle \sum _{k=0}^{n}2^{k}}$.
• Presenta autosimilitud exacta.
• Su dimensión de Hausdorff-Besicovitch es 2.^[4]​
• Se puede generar mediante el sistema de funciones iteradas no contractivo formado por las siguientes funciones:^[5]​

${\displaystyle f_{1}(x,y)=(x,y)}$

${\displaystyle f_{2}(x,y)={\frac {1}{2}}(x-y,x+y)+(0,1)}$

${\displaystyle f_{3}(x,y)={\frac {1}{2}}(x+y,-x+y)+\left({\frac {1}{2}},{\frac {3}{2}}\right)}$

• Si se elimina la primera función del sistema de funciones iteradas, se tiene un sistema contractivo que genera un fractal parecido a la curva C de Lévy.

Si se cambian los ángulos que forman los cuadrados (y, por tanto, sus tamaños), se obtienen otros árboles fractales. Por ejemplo, con ángulos de 60 y 30 grados y 9 iteraciones se tiene el siguiente árbol (en este ejemplo, el conjunto inicial es el borde de un cuadrado):

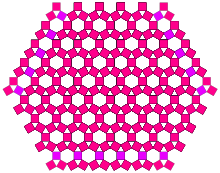Orden 4	Orden 10

Para los ángulos ${\displaystyle \alpha }$ y ${\displaystyle 90^{\circ }-\alpha }$, la razón de contracción de los cuadrados ha de ser ${\displaystyle cos(\alpha )}$ y ${\displaystyle sin(\alpha )}$, respectivamente.^[4]​

El árbol de Pitágoras fue construido por primera vez por el profesor de matemáticas Albert E. Bosman (1891-1961), en Holanda en 1942.^[6]​^[1]​

Es posible que el árbol de Pitágoras sería muy útil para antenas fractales con ajustes menores. Esta suposición se basa en la dimensión de Hausdorff-Besicovitch.

• Anexo:Fractales por dimensión de Hausdorff

• Wikimedia Commons alberga una categoría multimedia sobre Árbol de Pitágoras.
• Galería de árboles de Pitágoras
• Árboles de Pitágoras