Centro de homotecia

En geometría, un centro de homotecia (también llamado centro de semejanza o centro homotético) es un punto desde el cual se pueden ver al menos dos figuras geométricamente semejantes como dilatación o contracción la una de la otra. Si el centro es «externo», las dos figuras son directamente semejantes entre sí, y por lo tanto, sus ángulos tienen el mismo sentido de rotación. Si el centro es «interno», las dos figuras son imágenes especulares escaladas entre sí, y sus ángulos tienen sentido opuesto.

Si dos figuras geométricas poseen un centro homotético, son semejantes entre sí; en otras palabras, deben tener los mismos ángulos en los puntos correspondientes y diferir solo en su escala relativa. El centro homotético y las dos figuras no necesitan estar en el mismo plano; también se pueden relacionar mediante una proyección tridimensional desde un centro de homotecia.

Los centros de homotecia pueden ser externos o internos. Si el centro es interno, las dos figuras geométricas son imágenes escaladas especulares la una de la otra; en lenguaje técnico, tienen quiralidad opuesta. Un ángulo en el sentido de las agujas del reloj en una figura correspondería a un ángulo en el sentido contrario a las agujas del reloj en la otra. Por el contrario, si el centro es externo, las dos figuras son directamente semejantes entre sí; sus ángulos tienen el mismo sentido.

Los círculos son geométricamente semejantes entre sí y presentan simetría especular respecto a cualquier diámetro. Por lo tanto, un par de círculos poseen indistintamente ambos tipos de centros homotéticos, internos y externos, a menos que los centros sean coincidentes, o sus dos radios sean iguales. Estos casos excepcionales se tratan más adelante, según su posición general. Los dos centros de homotecia se encuentran en la línea que une los centros de las dos circunferencias dadas, que se llama la «recta de centros» (Figura 3). También se pueden incluir círculos con radio cero (véanse los casos excepcionales), y así mismo se puede usar el radio negativo, conmutando los centros externo e interno.

Para un par de círculos dados, los centros de homotecia internos y externos se pueden localizar de varias maneras. En geometría analítica, el centro de homotecia interno se obtiene como la media ponderada de los centros de los círculos, ponderados por el radio del círculo opuesto: la distancia desde el centro del círculo al centro interno es proporcional a ese radio, por lo que la ponderación es proporcional al radio opuesto. Denotando los centros de los círculos como ${\displaystyle C_{1}}$ y ${\displaystyle C_{2}}$ por ${\displaystyle (x_{1},y_{1})}$ y ${\displaystyle (x_{2},y_{2})}$ y sus radios por ${\displaystyle r_{1}}$ y ${\displaystyle r_{2}}$; y designando el centro por ${\displaystyle (x_{0},y_{0}),}$ esto es:

${\displaystyle (x_{0},y_{0})={\frac {r_{2}}{r_{1}+r_{2}}}(x_{1},y_{1})+{\frac {r_{1}}{r_{1}+r_{2}}}(x_{2},y_{2}).}$

El centro externo se puede calcular con la misma ecuación, pero considerando uno de los radios como negativo; cualquiera de los dos produce la misma ecuación, que es:

${\displaystyle (x_{e},y_{e})={\frac {-r_{2}}{r_{1}-r_{2}}}(x_{1},y_{1})+{\frac {r_{1}}{r_{1}-r_{2}}}(x_{2},y_{2}).}$

De manera más general, tomar ambos radios con el mismo signo (tanto positivo como negativo) produce el centro interno, mientras que tomar los radios con signos opuestos (uno positivo y el otro negativo) produce el centro externo. Nótese que la ecuación para el centro interno es válida para cualquier valor (a menos que ambos radios sean cero o uno sea el negativo del otro), pero la ecuación para el centro externo requiere que los radios sean diferentes, de lo contrario implica una división por cero.

En geometría sintética, se dibujan dos diámetros paralelos, uno para cada círculo; de manera que formen el mismo ángulo α con la línea de centros. Las rectas A₁A₂ y B₁B₂ dibujadas a través de los puntos finales correspondientes de esos radios, que son puntos homotéticos, se cruzan entre sí y con la línea de centros en el centro de homotecia externo. Por el contrario, las líneas A₁B₂ y B₁A₂ dibujadas a través de un punto final y el punto final opuesto en el otro círculo, se cruzan entre sí y con la línea de centros en el centro homotético interno.

Como caso límite de esta construcción, una línea tangente a ambos círculos (una línea bitangente) pasa a través de uno de los centros de homotecia, ya que forma ángulos rectos con los dos diámetros correspondientes, que son así paralelos; véase rectas tangentes a dos circunferencias para más detalles. Si los círculos quedan en lados opuestos de la recta, la tangente pasa a través del centro de homotecia interno, como en A₂B₁ en la figura anterior. Por el contrario, si los círculos quedan en el mismo lado de la línea, pasa a través del centro de homotecia externo (no representado).

Si los círculos tienen el mismo radio (pero centros diferentes), no poseen un centro homotético externo en el plano afín: en la geometría analítica esto da como resultado una división por cero, mientras que en la geometría sintética las líneas A₁A₂ y B₁B₂ son paralelas a la línea de centros (tanto para líneas secantes como para las líneas bitangentes) y, por lo tanto, no tienen intersección. Un centro externo se puede definir en el plano proyectivo como el punto del infinito correspondiente a la pendiente de esta línea. Este es también el límite del centro externo si los centros de los círculos están fijos y los radios se varían hasta que sean iguales.

Si los círculos tienen el mismo centro pero diferentes radios, tanto el externo como el interno coinciden con el centro común de los círculos. Esto se puede ver a partir de la fórmula analítica, y también es el límite de los dos centros homotéticos, ya que los centros de los dos círculos se pueden hacer variar hasta que coincidan, manteniendo los radios iguales. Sin embargo, no hay una línea de centros, y la construcción sintética falla cuando las dos líneas paralelas coinciden.

Si un radio es cero pero el otro es distinto de cero (un punto y un círculo), tanto el centro externo como el interno coinciden con el punto (centro del círculo de radio cero).

Si los dos círculos son idénticos (el mismo centro, el mismo radio), el centro interno es su centro común, pero no hay un centro externo bien definido. De manera adecuada, la función parametrizada de dos círculos en el plano hacia el centro externo tiene una discontinuidad no evitable en el lugar geométrico de los círculos idénticos. En el límite de dos círculos con el mismo radio pero distintos centros tendiendo a tener el mismo centro, el centro externo es el punto en el infinito correspondiente a la pendiente de la línea de centros, que puede ser cualquiera, por lo que no existe un límite para todos los posibles pares de tales círculos

Por el contrario, si ambos radios son cero (dos puntos) pero los puntos son distintos, el centro externo puede definirse como el punto en el infinito correspondiente a la pendiente de la línea de centros, pero no hay un centro interno bien definido.

En general, un rayo que emana de un centro homotético intersecará cada uno de sus círculos en dos puntos. De estos cuatro puntos, se dice que dos son «homólogos» si los radios dibujados forman el mismo ángulo con la línea que conecta los centros, por ejemplo, los puntos A₁ y A₂ en la Figura 3. Los puntos que son colineales con respecto al centro homotético pero que son «no» homólogos se dice que son «antihomólogos»,^[2]​ por ejemplo, los puntos Q y P′ en la Figura 4.

Cuando dos rayos del mismo centro homotético se cruzan con los dos círculos, cada conjunto de puntos antihomológicos se encuentra en un círculo.

Considérense los triángulos EQS y EQ′S′ (Figura 4).

Son semejantes porque ambos comparten el ángulo ∠QES = ∠Q′ES′ y ${\displaystyle {\frac {EQ}{EQ^{\prime }}}={\frac {ES}{ES^{\prime }}}}$ ya que E es el centro homotético. De esa semejanza se deduce que ∠ESQ = ∠ES′Q′ = α. El ángulo inscrito ∠EP′R′ = ∠ES′Q′. ∠QSR′ = 180°-α, ya que es suplementario a ∠ESQ. En el cuadrilátero QSR′P′ ∠QSR′ + ∠QP′R′ = 180° - α + α = 180° lo que significa que puede estar inscrito en una circunferencia. De la expresión de la potencia de un punto se deduce que EQ · EP′ = ES · ER′.

Del mismo modo, se puede demostrar que PRS′Q′ puede inscribirse en una circunferencia y EP · EQ′ = ER · ES′.

La prueba es similar para el centro homotético interno I.

PIR ~ P′IR′ luego ∠RPI = ∠IP′R′ = α. ∠RS′Q′ = ∠PP′R′ = α (teorema del ángulo inscrito). El segmento RQ′ se ve en el mismo ángulo desde P y S′, lo que significa que R, P, S′, Q′ se encuentran en un círculo.

De acuerdo con el teorema de las cuerdas secantes, IP · IQ′ = IR · IS′.

Del mismo modo QSP′R′ se puede inscribir en un círculo, e IQ · IP′ = IS · IR′.

Dos círculos tienen un eje radical, que es la línea de los puntos desde los que las tangentes a ambos círculos tienen la misma longitud. De manera más general, cada punto en el eje radical tiene la propiedad de que su potencia relativa a los círculos es la misma. El eje radical es siempre perpendicular a la línea de centros, y si se cruzan dos círculos, su eje radical es la línea que une sus puntos de intersección. Para tres círculos, se pueden definir tres ejes radicales, uno para cada par de círculos (C₁ / C₂, C₁ / C₃ y C₂ / C₃); notablemente, estos tres ejes radicales se cruzan en un solo punto, el centro radical. Las tangentes tendidas desde el centro radical a los tres círculos tendrían la misma longitud.

Se pueden usar dos pares de puntos antihomológicos para encontrar un punto en el eje radical. Considérense los dos rayos que emanan del centro homotético externo E en la Figura 4. Estos rayos intersecan los dos círculos dados (verde y azul en la Figura 4) en dos pares de puntos antihomólogos, Q y P′ para el primer rayo, y S y R′ para el segundo rayo. Estos cuatro puntos se encuentran en un solo círculo, que cruza ambos círculos dados. Por definición, la línea QS es el eje radical del nuevo círculo con el círculo dado verde, mientras que la línea P′R′ es el eje radical del nuevo círculo con el círculo dado azul. Estas dos líneas se cruzan en el punto G, que es el centro radical del nuevo círculo y los dos círculos dados. Por lo tanto, el punto G también se encuentra en el eje radical de los dos círculos dados.

Para cada par de puntos antihomólogos de dos círculos, existe un tercer círculo que es tangente a los dos círculos dados y que los toca en los puntos antihomólogos.

Lo contrario también es cierto: cada círculo que es tangente a otros dos círculos, los toca en un par de puntos antihomólogos.

Sean dos círculos dados, con centros O₁ y O₂ (Figura 5). E es su centro homotético externo. Se traza un rayo arbitrario desde E que cruza los dos círculos en P, Q, P′ y Q′. Extiéndase O₁Q y O₂P′ hasta que se intersequen en T₁. Se comprueba fácilmente que los triángulos O₁PQ y O₂P′Q′ son semejantes debido a su homotecia. También son triángulos isósceles porque O₁P = O₁Q (radio), y por lo tanto, ∠O₁PQ = ∠O₁QP = ∠O₂P& prime;Q′ = ∠O₂Q′P′ = T₁QP′ = ∠T₁P′Q. Así, T₁P′Q también es isósceles y se puede construir un círculo con el centro T₁ y el radio T₁P′ = T₁Q. Este círculo es tangente a los dos círculos dados en los puntos Q y P′.

La prueba para el otro par de puntos antihomólogos (P y Q′), así como en el caso del centro homotético interno es análoga.

Si se construyen los círculos tangentes para cada posible par de puntos antihomológicos, se obtienen dos familias de círculos, una para cada centro homotético. La familia de círculos del centro homotético externo es tal que cada círculo tangente contiene «los dos círculos dados» o ninguno (Figura 6). Por otro lado, los círculos de la otra familia siempre contienen solo uno de los círculos dados (Figura 7).

Todos los círculos de una familia tangente tienen un centro radical común y coincide con el centro homotético.
Para demostrarlo, considérense dos rayos del centro homotético, que se cruzan con los círculos dados (Figura 8). Existen dos círculos tangentes T₁ y T₂ que tocan los círculos dados en los puntos antihomológicos. Como ya se ha demostrado, estos puntos se encuentran en un círculo C y, por lo tanto, los dos rayos son ejes radicales para C / T₁ y C / T₂. Entonces, el punto de intersección de los dos ejes radicales también debe pertenecer al eje radical de T₁ / T₂. Este punto de intersección es el centro homotético E.

Si los dos círculos tangentes tocan pares colineales de puntos antihomólogos, como en la Figura 5, entonces debido a la homotecia ${\displaystyle {\frac {EP}{EP^{\prime }}}={\frac {EQ}{EQ^{\prime }}};{EP}\cdot {EQ^{\prime }}={EQ}\cdot {EP^{\prime }}}$. Por lo tanto, las potencias de E con respecto a los dos círculos tangentes son iguales, lo que significa que E pertenece al eje radical.

Cualquier par de círculos tiene dos centros de semejanza, por lo tanto, tres círculos tendrán seis centros de semejanza, dos para cada par distinto de círculos dados. Sorprendentemente, estos seis puntos se encuentran en cuatro líneas, tres puntos en cada línea. A continuación se demuestra:

Considérese el plano de los tres círculos (Figura 9). Desplácese cada punto central perpendicularmente al plano en una distancia igual al radio correspondiente. Los centros se pueden desplazar a cualquier lado del plano. Los tres puntos de compensación definen un solo plano. En ese plano se construyen tres rectas a través de cada par de puntos. Las líneas atraviesan el plano de círculos en los puntos «H_AB», H_BC y H_AC. Dado que el lugar geométrico de puntos que son comunes a dos planos distintos y no paralelos es una recta, necesariamente estos tres puntos se encuentran en dicha recta. A partir de la simejanza de triángulos H_ABAA′ y H_ABBB′ se observa que ${\displaystyle {\frac {H_{AB}B}{H_{AB}A}}={\frac {r_{B}}{r_{A}}}}$ (r_A,B es el radio de los círculos) y por lo tanto H_AB es de hecho el centro homotético de los dos círculos correspondientes. Se puede hacer lo mismo para H_BC y H_AC.

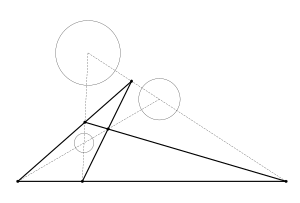
Repetir el procedimiento anterior para diferentes combinaciones de centros homotéticos (en el método empleado esto está determinado por el lado en el que se compensen los centros de los círculos) produciría un total de cuatro rectas, con tres centros homotéticos en cada recta (Figura 10).

A continuación se expone otra forma de probar esto:

Sean C₁ y C₂ un par de círculos conjugados tangentes a tres círculos determinados (Figura 11). Por conjugado se entiende que ambos círculos tangentes pertenecen a la misma familia con respecto a cualquiera de los pares de círculos dados. Como ya se ha visto, el eje radical de dos círculos tangentes de la misma familia pasa a través del centro homotético de los dos círculos dados. Como los círculos tangentes son comunes para los tres pares de círculos dados, todos sus centros homotéticos pertenecen al eje radical de C₁ y C₂, por ejemplo, se encuentran en una sola línea.

Esta propiedad se explota en la solución general ideada por Joseph Diaz Gergonne para el problema de Apolonio. Dados los tres círculos, se pueden encontrar los centros homotéticos y, por lo tanto, el eje radical de un par de círculos de la solución. Por supuesto, hay infinitos círculos con el mismo eje radical, por lo que se realiza un trabajo adicional para descubrir exactamente qué dos círculos son la solución.

• Teorema de Tales
• Semejanza (geometría)
• Homotecia
• Eje radical
• Centro radical
• Problema de Apolonio