Minimax

En teoría de juegos, 'minimax' es un método de decisión para minimizar la pérdida máxima esperada en juegos con adversario y con información perfecta. Minimax es un algoritmo recursivo.

El funcionamiento de minimax puede resumirse en cómo elegir el mejor movimiento para ti mismo suponiendo que tu contrincante escogerá el peor para ti.

Aunque existen evidencias de que Charles Babbage ya había trabajado antes sobre una idea similar,^[1]​ fue el matemático francés Émile Borel el primero en ofrecer en 1921 un tratamiento riguroso a los juegos competitivos y en estudiar las estrategias aplicables a los juegos de suma cero.^[2]​^[3]​ Sin embargo suele atribuirse a John von Neumann el principal mérito de la concepción del principio minimax, ya que fue él quien, en su artículo de 1928 «Zur Theorie der Gesellschaftsspiele» («Sobre la teoría de los juegos de sociedad») publicado en la revista Mathematische Annalen,^[4]​ puso las bases de la moderna teoría de juegos y probó el teorema fundamental del minimax, por el que se demuestra que para juegos de suma cero con Información perfecta entre dos competidores existe una única solución óptima.^[5]​

John von Neumann es el creador del teorema minimax, quien dio la siguiente noción de lo que era un juego:

Un juego es una situación conflictiva en la que uno debe tomar una decisión sabiendo

que los demás también toman decisiones, y que el resultado del conflicto se determina, de

algún modo, a partir de todas las decisiones realizadas.

También afirmó que:

Siempre existe una forma racional de actuar en juegos de dos participantes, si los intereses que los gobiernan son completamente opuestos.

La demostración a esa afirmación se llama teoría minimax y surge en 1928.

Este teorema establece que en los juegos bipersonales de suma cero, donde cada jugador conoce de antemano la estrategia de su oponente y sus consecuencias, existe una estrategia que permite a ambos jugadores minimizar la pérdida máxima esperada. En particular, cuando se examina cada posible estrategia, un jugador debe considerar todas las respuestas posibles del jugador adversario y la pérdida máxima que puede acarrear. El jugador juega, entonces, con la estrategia que resulta en la minimización de su máxima pérdida. Tal estrategia es llamada óptima para ambos jugadores sólo en caso de que sus minimaxes sean iguales (en valor absoluto) y contrarios (en signo). Si el valor común es cero el juego se convierte en un sinsentido.

En los juegos de suma no nula, existe tanto la estrategia minimax como la maximin. La primera intenta minimizar la ganancia del rival, es decir, busca que el rival tenga el peor resultado. La segunda intenta maximizar la ganancia propia, o sea busca que el jugador obtenga el mejor resultado.

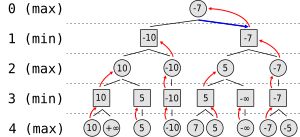
Pasos del algoritmo minimax:

1. Generación del árbol de juego. Se generarán todos los nodos hasta llegar a un estado terminal.
2. Cálculo de los valores de la función de utilidad para cada nodo terminal.
3. Calcular el valor de los nodos superiores a partir del valor de los inferiores. Según nivel si es MAX o MIN se elegirán los valores mínimos y máximos representando los movimientos del jugador y del oponente, de ahí el nombre de minimax.
4. Elegir la jugada valorando los valores que han llegado al nivel superior.

El algoritmo explorará los nodos del árbol asignándoles un valor numérico mediante una función de evaluación, empezando por los nodos terminales y subiendo hacia la raíz. La función de utilidad definirá lo buena que es la posición para un jugador cuando la alcanza. En el caso del ajedrez los posibles valores son (+1,0,-1) que se corresponden con ganar, empatar y perder respectivamente. En el caso del backgammon los posibles valores tendrán un rango de [+192,-192], correspondiéndose con el valor de las fichas. Para cada juego pueden ser diferentes.

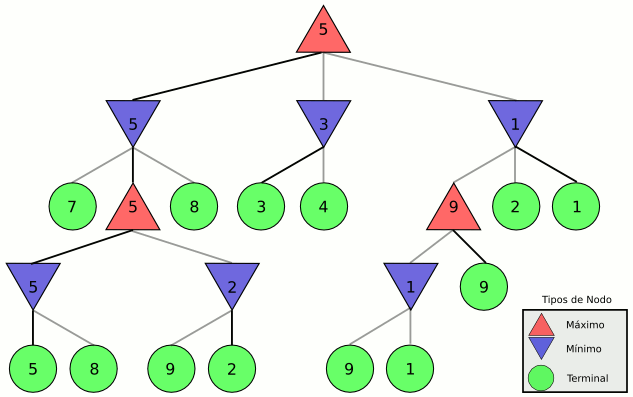
Si minimax se enfrenta con el dilema del prisionero escogerá siempre la opción con la cual maximiza su resultado suponiendo que el contrincante intenta minimizarlo y hacernos perder.

En el siguiente ejemplo puede verse el funcionamiento de minimax en un árbol generado para un juego imaginario. Los posibles valores de la función de utilidad tienen un rango de [1-9]. En los movimientos del contrincante suponemos que escogerá los movimientos que minimicen nuestra utilidad, en nuestros movimientos suponemos que escogeremos los movimientos que maximizan nuestra utilidad.

El primer paso será calcular los nodos terminales, en verde. Posteriormente calcularemos el cuarto nivel, movimiento min, minimizando lo elegido (5, 2 y 1). Después podremos calcular el tercer nivel, movimiento max, maximizando la utilidad (5, 9). El segundo nivel es un movimiento min (5, 3 y 1). Finalmente llegamos al primer nivel, el movimiento actual, elegiremos el nodo que maximice nuestra utilidad (5).

En la práctica el método minimax es impracticable excepto en supuestos sencillos. Realizar la búsqueda completa requeriría cantidades excesivas de tiempo y memoria.

Claude Shannon en su texto sobre ajedrez de 1950 (Programming a Computer for Playing Chess) propuso limitar la profundidad de la búsqueda en el árbol de posibilidades y determinar su valor mediante una función Heurística.

Para optimizar minimax puede limitarse la búsqueda por nivel de profundidad o por tiempo de ejecución. Otra posible técnica es el uso de la poda alfa-beta. Esta optimización se basa en evitar el cálculo de ramas cuya evaluación final no va a poder superar los valores previamente obtenidos.

En este artículo sobre videojuegos y matemáticas se detectaron varios problemas. Por favor, edítalo y/o discute los problemas en la discusión para mejorarlo: Necesita ser wikificado conforme a las convenciones de estilo de Wikipedia. Carece de fuentes o referencias que aparezcan en una fuente acreditada. Este aviso fue puesto el 16 de enero de 2010.

Negamax es una variante del algoritmo minimax donde cada nodo independientemente si fuese MIN o MAX toma el valor máximo de sus hijos (como si todos los nodo fueran MAX), solo que los valores de los nodos MAX se cambian de signo (de ahí su nombre, en vez de tomar máximos y mínimos toma siempre máximos pero con valores cambiados). De esta forma se logra el mismo efecto ya que tomar el mayor valor pero cambiado de signo es en realidad tomar el menor así cuando el algoritmo está en un nivel MIN cuando toma el mayor de sus hijos en realidad está tomando al menor.

La función Negamax podría recibir como parámetro un signo, de esta manera se podría comenzar por niveles MIN o niveles MAX, pero no necesariamente ya se puede establecer niveles estáticos, donde cada nivel está definido por un signo distinto.

Hablando del minimax: Suponiendo que existe min() que devuelve el menor y max() que devuelve el mayor, Negamax se basa en la siguiente igualdad matemática:

• max(x, y)=-min(-x,-y)

A este algoritmo también se le pueden aplicar podas y heurísticas para acortar su tiempo de ejecución, además existe una mejora de este algoritmo llamado negascout.

   int NegaMax(estado) {       if(estado_final(estado)) {            return evaluacion_heurística(estado);        }        max=-infinito;        while exist movimiento_posible(estado) {            val=-NegaMax(mover(mov, estado));            if (val>max) {                max=val;            }        }        return(max);    } 

Donde estado_final() verifica si se llegó a un estado de corte de recursión, evaluacion_heurística() devuelve el valor heurístico del nodo, movimiento_posible() es un movimiento dentro del sub-árbol de todos los movimientos posibles, mover() efectúa el movimiento para luego hacer un Backtracking.

• La teoría del minimax inspiró a Phillip K. Dick a escribir la novela «Solar lottery» («Lotería solar»).

• poda alfa-beta
• búsqueda de profundidad limitada
• profundización iterativa
• negamax
• expectimax
• transposition tables
• Montecarlo

• Beal, Donald F. (1999). The Nature of Minimax Search. Universidad de Maastricht: Institute of Knowledge and Agent Technology, UM. ISBN 90-62-16-6348. 
• Borel, Émile (1921). «La theorie du jeu et les equations integrales ä noyau symetrique». Comptes rendus de l'Académie des sciences. 
• Herik, Jaap van (1983). Computerschaak, Schaakwereld en Kunstmatige Intelligentie. La Haya: Delft University of Technology. Academic Service. ISBN 90-62-33-093-2. 
• Mosterín, Jesús (2000). Los lógicos. Madrid: Espasa Calpe. ISBN 84-239-9755-3. 
• Neumann, John von (1928). «Zur Theorie der Gesellschaftsspiele». Mathematische Annalen.  (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
• Wiener, Norbert (1948). Cybernetics: Or Control and Communication in the Animal and the Machine. Cambridge: MIT Press. ISBN 978-0-262-73009-9. 

• Ejemplo de implementación de MINIMAX en Clisp .
• Explicación Matemática de juegos bipersonales de suma nula y algoritmo minimax
• Algoritmo Minimax interactivo online

• «Strategy Game Programming». fierz.ch.  — Strategy Game Programming for board games such as Checkers and Chess