Romboedro

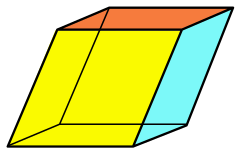

En geometría, un romboedro es una figura tridimensional, como un cubo, del que se diferencia porque sus 6 caras son rombos. Puede definirse como un poliedro de seis caras (hexaedro), todas ellas rombos idénticos. No se trata de un poliedro regular, porque aunque sus caras son todas iguales (uniformes), no son polígonos regulares.
Romboedro truncado
[editar]Un caso particular de romboedro es el que se halla truncado por sus vértices agudos, produciendo seis caras idénticas con forma de pentágono irregular, y dos caras triangulares regulares, paralelas entre sí. Es posible hacer que el poliedro tenga todos sus vértices en una esfera circunscrita.
Sólido de Durero
[editar]

Este poliedro a veces se denomina sólido de Durero, por su aparición en el grabado Melancolía I de 1514 de Alberto Durero. El gráfico formado por sus aristas y vértices se llama grafo de Durero.
La forma del sólido representado por Durero es tema de debate académico.[1] Según Lynch (1982), la hipótesis de que la forma es un cubo truncado fue propuesta por Strauss (1972); sin embargo, la mayoría de las fuentes están de acuerdo en que es el truncamiento de un romboedro. A pesar de este acuerdo, la geometría exacta de este romboedro es objeto de varias teorías contradictorias:
- Richter (1957) afirma que los rombos del romboedro a partir del cual se construye esta forma tienen una relación de 5:6 entre sus diagonales cortas y largas, según lo que los ángulos agudos de los rombos serían aproximadamente 80°.
- Schröder (1980) y Lynch (1982), en cambio, concluyen que la relación es √3:2 y que el ángulo es de aproximadamente de 82°.
- MacGillavry (1981) mide las características del dibujo y encuentra que el ángulo es de aproximadamente 79°. Él y un autor posterior, Wolf von Engelhardt (véase Hideko, 2009) argumentan que esta elección de ángulo proviene de su presencia física en los cristales de calcita.
- Schreiber (1999) argumenta, basado en los escritos de Durero, que todos los vértices del sólido de Durero se encuentran en una esfera común, y además afirma que los ángulos agudos del rombo son de 72°. Hideko (2009) enumera a varios otros estudiosos que también secundan la teoría de 72°, comenzando por Paul Grodzinski en 1955. Argumenta que esta teoría está menos motivada por el análisis del dibujo real, y más por los principios estéticos relacionados con los pentágonos regulares y la Sección Áurea.
- Weitzel (2004) analiza un boceto de Durero (1510) del mismo sólido, a partir del cual confirma la hipótesis de Schreiber de que la forma tiene una esfera circunscrita pero con ángulos de rombo de aproximadamente de 79,5°.
- Hideko, 2009 sostiene que la forma pretende representar una solución al famoso problema geométrico de duplicar el cubo, sobre el que también escribió Durero en 1525. Por lo tanto, concluye que (antes de cortar las esquinas) la forma es un cubo estirado por su diagonal larga. Más específicamente, argumenta que Durero dibujó un cubo real, con la diagonal larga paralela al plano de perspectiva, y luego amplió su dibujo por algún factor en la dirección de la diagonal larga; el resultado sería el mismo que si hubiera dibujado el sólido alargado. El factor de ampliación que es relevante para duplicar el cubo es 21/3 ≈ 1.253, pero Hideko deriva un factor de ampliación diferente que se ajusta mejor al dibujo, 1,277, de un modo más complicado.
- Futamura, Frantz y Crannell (2014) clasifican las soluciones propuestas para este problema según dos parámetros: el ángulo agudo y el nivel de corte, denominado relación cruzada. Su estimación de la relación cruzada es cercana a la de MacGillavry, y tiene un valor numérico cercano a la Sección Áurea. Basados en esto, postulan que el ángulo agudo es y que la relación entre las diagonales es exactamente (phi, o la sección aúrea).
Referencias
[editar]- ↑ Véase Weitzel (2004) y Ziegler (2014), de los que se ha tomado lo que sigue:
Bibliografía
[editar]- Lynch, Terence (1982), «The geometric body in Dürer's engraving Melencolia I», Journal of the Warburg and Courtauld Institutes (The Warburg Institute) 45: 226-232, JSTOR 750979, doi:10.2307/750979..
- MacGillavry, C. (1981), «The polyhedron in A. Dürers Melencolia I», Nederl. Akad. Wetensch. Proc. Ser. B 84: 287-294.. Citado por Weitzel (2004).
- Richter, D. H. (1957), «Perspektive und Proportionen in Albrecht Dürers "Melancholie"», Z. Vermessungswesen 82: 284-288 y 350-357.. Citado por Weitzel (2004).
- Schreiber, Peter (1999), «A new hypothesis on Dürer's enigmatic polyhedron in his copper engraving "Melencolia I"», Historia Mathematica 26: 369-377, doi:10.1006/hmat.1999.2245..
- Schröder, E. (1980), Dürer, Kunst und Geometrie, Dürers künstlerisches Schaffen aus der Sicht seiner "Underweysung", Basel.. Citado por Weitzel (2004).
- Strauss, Walter L. (1972), The Complete Engravings of Dürer, New York, p. 168, ISBN 0-486-22851-7.. Citado por Lynch (1982).
- Weber, P. (1900), Beiträge zu Dürers Weltanschauung—Eine Studie über die drei Stiche Ritter, Tod und Teufel, Melancholie und Hieronymus im Gehäus, Strassburg.. Citado por Weitzel (2004).
- Weitzel, Hans (2004), «A further hypothesis on the polyhedron of A. Dürer's engraving Melencolia I», Historia Mathematica 31 (1): 11-14, doi:10.1016/S0315-0860(03)00029-6..
- Hideko, Ishizu (2009), «Another solution to the polyhedron in Dürer's Melencolia: A visual demonstration of the Delian problem», Aesthetics (The Japanese Society for Aesthetics) 13: 179-194..
- Ziegler, Günter M. (3 de diciembre de 2014), «Dürer's polyhedron: 5 theories that explain Melencolia's crazy cube», Alex Bellos's Adventures in Numberland, The Guardian..
- Futamura, F.; Frantz, M.; Crannell, A. (2014), «The cross ratio as a shape parameter for Dürer's solid», Journal of Mathematics and the Arts 8 (3-4): 111-119, arXiv:1405.6481, doi:10.1080/17513472.2014.974483..
Enlaces externos
[editar]- Esta obra contiene una traducción derivada de «Truncated triangular trapezohedron» de Wikipedia en inglés, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

