Símbolo de Wythoff

En la geometría, el símbolo de Wythoff es una notación representando una construcción de Wythoff de un poliedro uniforme o una teselación del plano dentro de un triángulo de Schwarz. Fue utilizado por primera vez por Coxeter, Longuet-Higgins y Miller en su enumeración de los poliedros uniformes. Más tarde, el diagrama de Coxeter se desarrolló para denotar politopos y panales uniformes en el espacio n-dimensional construidos a partir de un símplex fundamental.

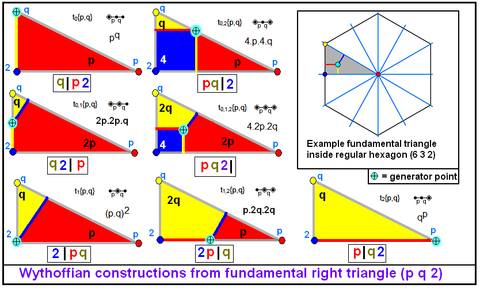
Un símbolo de Wythoff consta de tres números y una barra vertical. Representa un poliedro o mosaico uniforme, aunque el mismo mosaico/poliedro puede tener diferentes símbolos de Wythoff a partir de diferentes generadores de simetría. Por ejemplo, el cubo regular se puede representar por 3 | 2 4 a partir de su simetría O_h, por 2 | 4 2 al representarse como un prisma cuadrado con 2 colores y simetría D_4h, así como por 2 2 2 | al representarse como una figura con 3 colores y simetría D_2h.

Con una ligera extensión, el símbolo de Wythoff puede aplicarse a todos los poliedros uniformes. Sin embargo, los métodos de construcción no producen todas las teselaciones uniformes en el espacio euclídeo o hiperbólico.

La construcción de Wythoff comienza al elegir un punto generador en un triángulo fundamental. Si la distancia de este punto desde cada uno de los lados no es cero, el punto debe elegirse para que esté a una distancia igual de cada borde. Luego, se deja caer una línea perpendicular entre el punto generador y cada cara en la que no se encuentra.

Los tres números en el símbolo de Wythoff, p, q y r, representan las esquinas del triángulo de Schwarz utilizadas en la construcción, que son ^π⁄_p, ^π⁄_q, y ^π⁄_r radianes respectivamente. El triángulo también se representa con los mismos números, escritos (p q r). La barra vertical en el símbolo especifica una posición categórica del punto generador dentro del triángulo fundamental de acuerdo con lo siguiente:

• p | q r indica que el generador se encuentra en la esquina p,
• p q | r indica que el generador se encuentra en el borde entre p y q,
• p q r | indica que el generador se encuentra en el interior del triángulo.

En esta notación, los espejos están etiquetados por el orden de reflexión del vértice opuesto. Los valores p, q, r se enumeran antes de la barra si el espejo correspondiente está activo.

Un uso especial es el símbolo | p q r, que se designa para el caso donde todos los espejos están activos, pero las imágenes reflejadas con números impares se ignoran. La figura resultante solamente tiene simetría rotacional.

El punto generador puede estar encendido o apagado en cada espejo, activado o no. Esta distinción crea 8 (2³) formas posibles, exceptuando una donde el punto generador está en todos los espejos.

El símbolo de Wythoff es funcionalmente similar al diagrama más general de Diagrama de Coxeter-Dynkin, en el que cada nodo representa un espejo y los arcos entre ellos, marcados con números, los ángulos entre los espejos. (Se omite un arco que representa un ángulo recto.) Un nodo se encierra en un círculo si el punto generador no está en el espejo.

Los triángulos fundamentales se dibujan en colores alternos como imágenes espejo. La secuencia de triángulos (p 3 2) cambia de esférica (p = 3, 4, 5) a eucliídea (p = 6) a hiperbólica (p ≥ 7). Las teselaciones hiperbólicas se muestran como una proyección de disco de Poincaré .

Símbolo de Wythoff	q | p 2	2 q | p	2 | p q	2 p | q	p | q 2	p q | 2	p q 2 |	| p q 2
Diagrama de Coxeter
Disposición de vértices	pq	q.2p.2p	p.q.p.q	p.2q.2q	qp	p.4.q.4	4.2p.2q	3.3.p.3.q
Triángulos fundamentales	7 formas + roma
(4 3 2)	3 | 4 2 43	2 3 | 4 3.8.8	2 | 4 3 3.4.3.4	2 4 | 3 4.6.6	4 | 3 2 34	4 3 | 2 3.4.4.4	4 3 2 | 4.6.8	| 4 3 2 3.3.3.3.4
(5 3 2)	3 | 5 2 53	2 3 | 5 3.10.10	2 | 5 3 3.5.3.5	2 5 | 3 5.6.6	5 | 3 2 35	5 3 | 2 3.4.5.4	5 3 2 | 4.6.10	| 5 3 2 3.3.3.3.5
(6 3 2)	3 | 6 2 63	2 3 | 6 3.12.12	2 | 6 3 3.6.3.6	2 6 | 3 6.6.6	6 | 3 2 36	6 3 | 2 3.4.6.4	6 3 2 | 4.6.12	| 6 3 2 3.3.3.3.6
(7 3 2)	3 | 7 2 73	2 3 | 7 3.14.14	2 | 7 3 3.7.3.7	2 7 | 3 7.6.6	7 | 3 2 37	7 3 | 2 3.4.7.4	7 3 2 | 4.6.14	| 7 3 2 3.3.3.3.7
(8 3 2)	3 | 8 2 83	2 3 | 8 3.16.16	2 | 8 3 3.8.3.8	2 8 | 3 8.6.6	8 | 3 2 38	8 3 | 2 3.4.8.4	8 3 2 | 4.6.16	| 8 3 2 3.3.3.3.8
(∞ 3 2)	3 | ∞ 2 ∞3	2 3 | ∞ 3.∞.∞	2 | ∞ 3 3.∞.3.∞	2 ∞ | 3 ∞.6.6	∞ | 3 2 3∞	∞ 3 | 2 3.4.∞.4	∞ 3 2 | 4.6.∞	| ∞ 3 2 3.3.3.3.∞

• Politopo regular
• Poliedro regular
• Lista de teselaciones uniformes
• Teselaciones uniformes en el plano hiperbólico
• Lista de poliedros uniformes
• Lista de poliedros uniformes por triángulo de Schwarz
• Listas de teselaciones uniformes en la esfera, el plano y el plano hiperbólico

• Coxeter Regular Polytopes, tercera edición, (1973), edición de Dover, ISBN 0-486-61480-8 (Capítulo V: El Caleidoscopio, Sección: 5.7 Construcción de Wythoff)
• Coxeter La belleza de la geometría: doce ensayos, Dover Publications, 1999, ISBN 0-486-40919-8 (Capítulo 3: Construcción de Wythoff para politopos uniformes)
• Coxeter, Longuet-Higgins, Miller, Poliedros uniformes, Phil. Trans. 1954, 246 A, 401–50.
• Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.  Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.  Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.  páginas.   9-10.

• Esta obra contiene una traducción derivada de «Wythoff symbol» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.