Tetradecágono

| Tetradecágono | ||
|---|---|---|
 Un tetradecágono regular | ||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 14 | |
| Vértices | 14 | |
| Grupo de simetría | , orden 2x14 | |
| Símbolo de Schläfli | {14}, t{7} (tetradecágono regular) | |
| Diagrama de Coxeter-Dynkin | | |
| Polígono dual | Autodual | |
| Área | (lado ) | |
| Ángulo interior | 154+2/7° ≈ 154,285714 | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
En geometría, un tetradecágono es un polígono de 14 lados y 14 vértices.[1]
Propiedades
[editar]Un tetradecágono tiene 77 diagonales, resultado que se puede obtener aplicando la ecuación general para determinar el número de diagonales de un polígono, ; siendo el número de lados , se tiene que:
La suma de todos los ángulos internos de cualquier tetradecágono es 2160 grados o radianes.
Tetradecágono regular
[editar]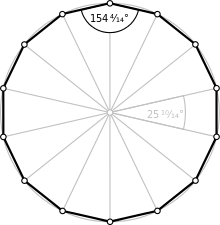
Un tetradecágono regular es el que tiene todos sus lados de la misma longitud y todos sus ángulos internos iguales. Cada ángulo interno del tetradecágono regular mide aproximadamente 154,29º o exactamente rad. Cada ángulo externo del tetradecágono regular mide aproximadamente 25,71º o exactamente rad.
Para obtener el perímetro P de un tetradecágono regular, multiplíquese la longitud t de uno de sus lados por catorce (el número de lados n del polígono).
El área A de un tetradecágono regular se calcula a partir de la longitud t de uno de sus lados con la siguiente fórmula:
donde es la constante pi y es la función tangente calculada en radianes.
Si se conoce la longitud de la apotema a del polígono, otra alternativa para calcular el área es:
Simetría
[editar]

El tetradecágono regular posee simetría diedral Dih14 de orden 28. Cuenta con 3 simetrías diedrales de subgrupo: Dih7, Dih2 y Dih1, y 4 simetrías cíclicas: Z14, Z7, Z2 y Z1. Estas 8 simetrías (el grupo y sus siete subgrupos) adoptan la forma de 10 simetrías distintas en el tetradecágono, un número mayor debido a que los ejes de simetría pueden atravesar tanto vértices como centros de aristas.
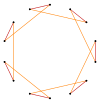
John Conway clasificó estas simetrías usando una letra y el orden de la simetría a continuación. Asignó la letra r al grupo de simetría de la figura regular; y en el caso de los subgrupos utilizó la letra d (de diagonal) para las figuras con ejes de simetría solo a través de sus vértices; p para figuras con ejes de simetría solo a través de ejes perpendiculares a sus lados; i para figuras con ejes de simetría tanto a través de vértices como a través de centros de lados; y g para aquellas figuras solo con simetría rotacional. Con a1 se etiquetan aquellas figuras con ausencia de simetría. Los tipos de simetrías más bajos permiten disponer de uno o más grados de libertad para definir distintas figuras irregulares.[2] Solo el subgrupo g14 no tiene grados de libertad, pero puede verse como un grafo dirigido. (Véase un ejemplo en la Teoría de grupos de John Conway)
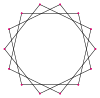
Los tetradecágonos irregulares de mayor simetría son d14, un tetradecágono isogonal construido mediante siete reflexiones que pueden alternar lados largos y cortos, y p14, un tetradecágono isotoxal, construido con longitudes de borde iguales, pero con vértices alternando dos ángulos internos diferentes. Estas dos formas son duales entre sí y tienen la mitad del orden de simetría del tetradecágono regular.
Disección
[editar] Proyección de un hipercubo |  Disección en 84 rombos |
Harold Scott MacDonald Coxeter estableció que cada zonágono (un 2m-gono cuyos lados opuestos son paralelos y de igual longitud) se puede diseccionar en m(m-1)/2 paralelogramos.[3] En particular, esto es cierto para polígonos regulares con muchos lados iguales, en cuyo caso los paralelogramos son todos rombos. Para el tetradecágono regular, m=7, y se puede dividir en 21: 3 conjuntos de 7 rombos. Esta descomposición se basa en una proyección en forma de polígono de Petrie de un hepteracto, con 21 de 672 caras. La lista A006245 define el número de soluciones como 24698, incluidas rotaciones de hasta 14 lóbulos y formas quirales en reflexión.
 |  | 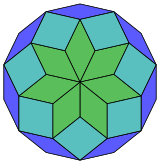 | 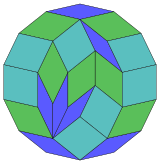 |  | 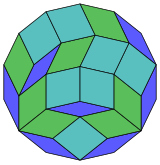 |
Uso numismático
[editar]- El tetradecágono regular se usa como la forma de algunas monedas conmemorativas de oro y plata de Malasia, por el número de lados que representa los 14 estados de la Federación de Malasia.[4]
Figuras relacionadas
[editar]
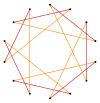
Un tetradecagrama es un polígono con forma de estrella de 14 lados, representado por el símbolo {14/n}. Hay dos estrellas regulares: {14/3} y {14/5}, usando los mismos vértices, pero conectando cada tercer o quinto punto. También hay tres compuestos: {14/2} se reduce a 2{7} como dos heptágonos, mientras que {14/4} y {14/6} se reducen a 2{7/2} y 2{7/3} como dos heptagramas diferentes, y finalmente {14/7} se reduce a siete dígonos.
Una aplicación notable de una estrella de catorce puntas está en la bandera de Malasia, que incorpora un tetradecagrama amarillo {14/6} en la esquina superior derecha, que representa la unidad de los trece estados con el gobierno federal.
Los truncamientos más profundos del heptágono regular y del heptagrama pueden producir formas de tetradecagrama intermedio isogonal (figura isogonal) con vértices igualmente espaciados y dos longitudes de arista. Otros truncamientos pueden formar polígonos de doble cobertura 2{p/q}, a saber: t{7/6} = {14/6} = 2{7/3}, t{7/4} = {14/4} = 2{7/2} y t{7/2} = {14/2} = 2{7}.[5]
Polígonos de Petrie
[editar]Los tetradecágonos regulares alabeados existen como polígonos de Petrie para muchos politopos de dimensiones superiores, que se muestran en proyecciones oblicuas, que incluyen:
| Polígonos de Petrie | ||||
|---|---|---|---|---|
| B7 | 2I2(7) (4D) | |||
 7-ortoplex |  hepteracto | 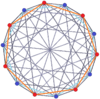 7-7 duopirámide |  7-7 duoprisma | |
| A13 | D8 | E8 | ||
 símplex | 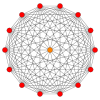 511 |  151 | 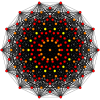 421 |  241 |
Referencias
[editar]- ↑ Weisstein, Eric W. „Heptagon.“ From MathWorld, A Wolfram Web Resource.
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
- ↑ Harold Scott MacDonald Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
- ↑ The Numismatist, Volume 96, Issues 7-12, Page 1409, American Numismatic Association, 1983.
- ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
Enlaces externos
[editar] Wikimedia Commons alberga una categoría multimedia sobre tetradecágonos.
Wikimedia Commons alberga una categoría multimedia sobre tetradecágonos.