Stringiteooria

Stringiteooria on teoreetilise füüsika suund, mis uurib mitte punktosakeste[1], vaid ühemõõtmelise ulatuvusega objektide, nn stringide dünaamikat ja vastastikmõjusid.[2] Stringiteooria kasutab nii kvantmehaanika kui ka relatiivsusteooria ideid, sellepärast luuakse tulevane kvantgravitatsiooni teooria võib-olla stringiteooria baasil.[3][4]
Stringiteooria põhineb hüpoteesil[5], et kõik elementaarosakesed ja nende fundamentaalsed vastastikmõjud tekivad ultramikroskoopiliste stringide võnkumiste ja vastastikmõjude (Plancki pikkuse suurusjärgus 10−35 m) tulemusena[2]. See lähenemine võimaldab ühest küljest vältida niisuguseid väljade kvantteooria raskusi nagu renormeerimine[6], teisest küljest aitab aga aine ja aegruumi ehitust põhjalikumalt selgitada[6].
Stringide kvantteooria tekkis 1970. aastate alguses hadronite ehituse stringimudelitega seotud Gabriele Veneziano valemite[7] mõtestamise tulemusena. 1980. aastate keskel ja 1990. aastatel arenes stringiteooria tormiliselt, oodati, et lähemal ajal formuleeritakse stringiteooria alusel nn kõige teooria[4], mida Albert Einstein oli aastakümneid edutult otsinud[8]. Ent vaatamata teooria matemaatilisele rangusele ja terviklikkusele ei ole seni leitud variante stringiteooria eksperimentaalseks kinnitamiseks[2].
Katsetel kirjeldada stringiteooriate redutseerimist ruumist mõõtmega 26 või 10[9] madalate energiate füüsika neljamõõtmelisse ruumi tekib muu hulgas probleem, et lisamõõtmeid saab kompaktifitseerida Calabi-Yau muutkondadele ja orbikondadele, mis tõenäoliselt on Calabi-Yau ruumide osalised piirjuhtumid, väga mitmel moel[10]. Võimalike lahenduste suur hulk alates 1970. aastate lõpust ja 1980. aastate algusest tekitas probleemi, mida tuntakse maastikuprobleemi nime all[11] ja mille tõttu mõned teadlased kahtlevad, kas stringiteooria väärib teadusliku teooria staatust[12].
Vaatamata nendele raskustele on stringiteooria stimuleerinud matemaatiliste formalismide, põhiliselt algebralise geomeetria, diferentsiaalgeomeetria ja topoloogia arengut ning on võimaldanud sügavamalt mõista varasemate kvantgravitatsiooni teooriate struktuuri[2]. Stringiteooria areng jätkub ja on lootust, et stringiteooriate puuduvad elemendid ja vastavad fenomenid leitakse lähemas tulevikus, sealhulgas Suurel Hadronite Põrgutil tehtavate katsete tulemusel[13].
Põhiteesid
[muuda | muuda lähteteksti]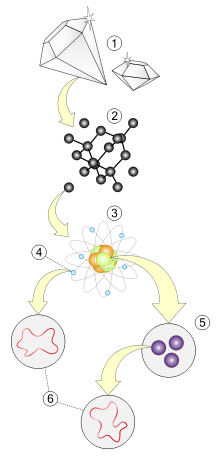
1. Makroskoopiline tasand – aine
2. Molekulide tasand
3. Aatomitasand – prootonid, neutronid ja elektronid
4. Subatomaarne tasand – elektron
5. Subatomaarne tasand – kvargid
6. Stringitasand
Kui oleks olemas eksplitsiitne mehhanism stringide ekstrapoleerimiseks madalate energiate füüsikasse, siis esitaks stringiteooria kõik fundamentaalosakesed ja nende vastastikmõjud kitsendustena mittelokaalsete ühemõõtmeliste objektide (stringide) ergastuste spektritele. Kompaktifitseeritud stringide iseloomulikud mõõtmed on erakordselt väikesed, suurusjärgus 10−33 cm (Plancki pikkuse suurusjärgus)[14], sellepärast nad ei ole katses vaadeldavad[2]. Analoogselt pillikeelte võnkumistega on stringide spektraalkomponendid võimalikud ainult teatud sageduste (kvantamplituudide) korral. Mida suurem on sagedus, seda suurem on võnkumisse akumuleerunud energia[15], ja vastavalt valemile E=mc², seda suurem on selle osakese mass, millena võnkuv string vaadeldavas maailmas ilmneb. Parameetriks, mis on analoogne ostsillaatori sagedusega, on stringi puhul massi ruut[16].
Kooskõlalised stringide kvantteooriad on võimalikud ainult kõrgemamõõtmelistes ruumides (mõõtmega üle 4, kui arvestada aega). Seoses sellega on stringifüüsikas lahtine aegruumi mõõtme küsimus[17]. Seda, et makromaailmas (vahetult vaadeldavas maailmas) ei ole lisamõõtmed vaadeldavad, seletatakse stringiteooriates ühega kahest võimalikust mehhanismist: 1) nende mõõtmete kompaktifikatsiooniga – kõverdumisega Plancki pikkuse suurusjärguni; 2) paljumõõtmelise universumi (multiversumi) kõigi osakeste lokaliseerumisega neljamõõtmelisel maailmalehel, mis ongi multiversumi vaadeldav osa. Oletatakse, et kõrgemad mõõtmed võivad ilmneda elementaarosakeste vastastikmõjudes kõrgetel energiatel, kuid seni pole seda täheldatud.
Stringiteooria konstrueerimisel eristatakse lähenemist primaarse ja sekundaarse kvantiseerimise kaudu. Viimane opereerib stringivälja mõistega − see on funktsionaal silmuste ruumil, sarnaselt väljade kvantteooriaga. Primaarse kvantiseerimise formalismis kirjeldatakse matemaatiliste meetoditega proovistringi liikumist välistes stringiväljades, seejuures ei välistata stringidevahelist vastastikmõju, sealhulgas stringide lagunemist ja ühinemist. Primaarse kvantiseerimise kaudu lähenemine seob stringiteooriat tavalise väljateooriaga maailmapinnal[4].
Kõige realistlikumate stringiteooriate kohustuslik element on supersümmeetria, sellepärast nimetatakse selliseid teooriaid superstringiteooriateks[18]. Osakeste ja nendevaheliste vastastikmõjude komplekt, mis on vaadeldav suhteliselt madalate energiate korral, praktiliselt reprodutseerib osakestefüüsika standardmudeli struktuuri, kusjuures paljud standardmudeli omadused saavad superstringiteooriate raames elegantse seletuse. Siiski pole seniajani printsiipe, mille abil võiks seletada stringiteooriate ühtesid või teisi kitsendusi, mis on vajalikud standardmudelisarnase teooria saamiseks[19].
1980. aastate keskel jõudsid Michael Green ja John Schwarz järeldusele, et supersümmeetria, mis on stringiteooria keskne lüli, saab selle koosseisu lülitada mitte ühel, vaid kahel viisil: esiteks ringi maailmapinna supersümmeetriana[4], teiseks aegruumi supersümmeetriana[20]. Need supersümmeetria sissetoomise viisid seovad konformse väljateooria meetodid väljade kvantteooria standardsete meetoditega[21][22]. Supersümmeetria sissetoomise nende viiside tehnilised iseärasused tingisid viie erineva superstringiteooria (tüüp I, tüübid IIA ja IIB ning kaks heterootilist stringiteooriat) tekkimise[23]. Selle tagajärjel tekkinud huvi kasvu stringiteooria vastu nimetatakse esimeseks superstringirevolutsiooniks. Kõik need mudelid realiseeritakse 10-mõõtmelises aegruumis, kuid nad erinevad stringispektrite ja sümmeetria kalibratsioonirühmade poolest. 1970. aastatel loodud ja 1980. aastatel arendatud 11-mõõtmelise supergravitatsiooni konstruktsioon[24] ning faasimuutujate ebatavalised topoloogilised duaalsused stringiteoorias viisid 1990. aastate keskel teise superstringirevolutsioonini. Selgus, et kõik neid teooriad on tegelikult tänu teatud duaalsustele omavahel tihedalt seotud.[25] Püstitati hüpotees, et kõik viis teooriat on ühe fundamentaalse teooria (M-teooria) piirjuhtumid. Praegu otsitakse adekvaatset matemaatilist keelt selle formuleerimiseks.[19]
Ajalugu
[muuda | muuda lähteteksti]Stringid hadronite füüsikas
[muuda | muuda lähteteksti]
Stringid kui fundamentaalobjektid toodi sisse kõigepealt osakestefüüsikas hadronite, eriti piionite ehituse seletamiseks.
1960. aastatel avastati sõltuvus hadroni spinni ja tema massi vahel (Chew'-Frautschi graafik)[26][27]. Selle vaatluse ajendil loodi Regge teooria, mille raames ei vaadeldud eri hadroneid mitte elementaarosakestena, vaid ühtse ulatuva objekti (redžeoni) ilmingutena. Järgnevatel aastatel tuletati Gabriele Veneziano, Yōichirō Nambu, Holger Bech Nielseni ja Leonard Susskindi töö tulemusena redžeonide hajumise valem ning anti seejuures aset leidvatele nähtustele stringidel põhinev tõlgendus.
1968. aastal avastasid Gabriele Veneziano ja Mahiko Suzuki, kes püüdsid analüüsida piionite kokkupõrkeid, et kõrge energiaga piionite paari hajumise amplituudi kirjeldab üsna hästi üks beetafunktsioonidest. Hiljem selgus, et piionite paari hajumise amplituudi saab arendada lõpmatusse ritta, mille algus langeb kokku Veneziano-Suzuki valemiga[28].
1970. aastal esitasid Yōichirō Nambu, Tetsuo Gotō, Holger Bech Nielsen ja Leonard Susskind idee, et põrkuvate piionite vaheline vastastikmõju tekib selle tõttu, et neid piioneid ühendab "lõpmata peen võnkuv niit". Eeldades, et see "niit" allub kvantmehaanikaseadusele, tuletasid nad valemi, mis langeb kokku Veneziano-Suzuki valemiga. Nii ilmusid mudelid, milles elementaarosakesi kujutatakse ühemõõtmeliste stringidena, mis vibreerivad teatud sagedustel.[28]
Kui saabus kvantkromodünaamika ajastu, kaotas teadlaste kogukond huvi stringiteooria vastu hadronite füüsikas kuni 1980. aastateni.[2]
Stringide bosonteooria
[muuda | muuda lähteteksti]Aastaks 1974 sai selgeks, et Veneziano valemitel põhinevad stringiteooriad realiseeruvad ruumi mõõtmes, mis on suurem kui 4: Veneziano mudel ja Shapiro-Virasoro mudel (S-V) mõõtmes 26 ning Ramondi-Neveu-Schwarzi mudel (R-NS) mõõtmes 10, ja kõik nad ennustavad tahhüone[29]. Tahhüonide kiirus ületab valguse kiiruse, mistõttu on nende olemasolu vastuolus põhjuslikkuse printsiibiga, mida aga mikromaailmas rikutakse. Seega ei ole mingeid veenvaid (esmajoones eksperimentaalseid) tahhüoni olemasolu tõestusi ega ka selle loogiliselt haavamatuid kummutusi[30]. Praegu peetakse paremaks mitte kasutada füüsikateooriate konstrueerimiseks tahhüonide ideed. Tahhüonide probleemi lahendus põhineb Wessi ja Zumino (1974) töödel aegruumi globaalsest (koordinaatidest sõltumatust) supersümmeetriast.[31] Aastal 1977 tõid Gliozzi, Sherk ja Olive mudelisse R-NS sisse spetsiaalse projektsiooni (GSO-projektsiooni) stringimuutujate jaoks, mis võimaldas tahhüoni kõrvaldada ning andis sisuliselt supersümmeetrilise stringi.[32] Aastal 1981 õnnestus Greenil ja Schwarzil kirjeldada GSO-projektsiooni D-mõõtmelise supersümmeetria terminites ja pisut hiljem tuua sisse kvantanomaaliate kõrvaldamise printsiibi stringiteooriates[33].
Aastal 1974 avastasid John Schwarz ja Joël Sherk ning nendest sõltumatult Tamiaki Yoneya mõningaid stringivibratsioone uurides, et nad vastavad täpselt hüpoteetilise gravitatsioonivälja kvandi (gravitoni) omadustele[34]. Schwarz ja Sherk väitsid, et stringiteooria ebaõnnestus alguses sellepärast, et teadlasid alahindasid selle mastaapi[19]. Selle mudeli alusel loodi bosonstringide teooria[4], mis on seniajani esimene stringiteooria variant, mida üliõpilastele õpetatakse[35]. See teooria formuleeritakse Aleksandr Poljakovi mõju terminites; selle abil saab ennustada stringi liikumist ruumis ja ajas. Poljakovi mõju kvantiseerimise protseduur viib selleni, et string võib vibreerida eri viisidel ja iga tema vibratsiooniviis genereerib eraldi elementaarosakese. Osakese massi ja tema vastastikmõju karakteristikud määrab stringi vibratsiooniviis. Nii saadavat gammat nimetatakse stringiteooria massispektriks.
Algsetes mudelites figureerisid nii lahtised stringid (niidid, millel on kaks vaba otsa) kui ka kinnised ringid (silmused). Kõik tänapäeva stringiteooriad ei kasuta mõlemat tüüpi, mõned ajavad läbi kinniste stringidega.
Bosonstringide teooria ei ole probleemideta. Esiteks on tal fundamentaalne ebastabiilsus, mis eeldab aegruumi enda lagunemist.
Peale selle, osakeste spekter piirdub bosonitega. Kuigi bosonid on Universumi tähtis koostisosa, ei koosne ta ainult nendest. Samuti ennustab ta mitteeksisteerivat osakest tahhüoni, mille massi ruut on negatiivne[16]. Selle uurimine, kuidas saab teooria spektrisse lülitada fermionid, viis supersümmeetria mõisteni: see on bosonite ja fermionide vahelise vastastikune seos, mille teoorial on praegu stringiteooriast sõltumatu tähtsus. Teooriaid, mis hõlmavad stringide fermionvibratsioone, nimetatakse superstringiteooriateks.[36]
Superstringirevolutsioonid
[muuda | muuda lähteteksti]

Aastatel 1984–1986 mõistsid füüsikud, et stringiteooria võiks kirjeldada kõiki elementaarosakesi ja nendevahelisi vastastikmõjusid, ja sajad teadlased hakkasid tööle stringiteooria alal, pidades seda füüsikateooriate ühendamise kõige perspektiivikamaks ideeks. Sellele esimesele superstringirevolutsioonile pani aluse Michael Greeni ja John Schwarzi 1984. aasta avastus, et I tüüpi stringiteoorias anomaaliad taanduvad. Selle taandumise mehhanismi nimetatakse Greeni-Schwarzi mehhanismiks. Teised olulised avastused, näiteks heterootilise stringi avastamine, tehti 1985.[19]
1990. aastate keskel avastasid Edward Witten, Joseph Polchinski jt füüsikud kaalukad tõendid selle kohta, et erinevad superstringiteooriad on seni välja töötamata 11-mõõtmelise M-teooria piirjuhtumid. See avastus märgistas teise superstringirevolutsiooni. Viimased stringiteooria (täpsemalt, M-teooria) uurimused puudutavad D-braane, paljumõõtmelisi objekte, mille olemasolu järeldub teooriasse lahtiste stringide sissetoomisest[19].
Aastal 1997 avastas Juan Maldacena seose stringiteooria ja kalibratsiooniteooria vahel, mida nimetatakse N=4-supersümmeetriliseks Yangi-Millsi teooriaks[4]. See seos, mida nimetatakse AdS/CFT-vastavuseks (lühend terminitest anti de Sitter space (anti-de-Sitteri ruum) ja conformal field theory (konformne väljateooria)), äratas stringiteoreetikute seas suurt tähelepanu ja praegu uuritakse seda intensiivselt[37]. AdS/CFT-vastavus on holograafilise printsiibi konkreetne realisatsioon, millel on kaugeleulatuvad järelmid mustade aukude kohta, lokaalsuse ja informatsiooni kohta füüsikas ning ka gravitatsioonilise vastastikmõju kohta.
Aastal 2003 algatas stringiteooria maastiku (eksponentsiaalselt suure arvu mitteekvivalentsete valevaakumite olemasolu) avastamine[38][39][40] diskussiooni selle kohta, mida võib stringiteooria kokkuvõttes ennustada ja kuidas stringikosmoloogia saab muutuda (#Falsifitseeritavus ja maastikuprobleem).
Artikli kirjutamine on selles kohas pooleli jäänud. Jätkamine on kõigile lahkesti lubatud. |
Viited
[muuda | muuda lähteteksti]- ↑ А. А. Комар. «Размер» элементарной частицы. – А. М. Прохоров (toim). Физическая энциклопедия, М., Советская энциклопедия: 1988, kd 2.
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 Гросс, Дэвид. Грядущие революции в фундаментальной физике. Projekt "Elemendid", teised avalikud loengud füüsikast (25.04.2006).
- ↑ Sunil Mukhi The Theory of Strings: A Detailed Introduction, 1999.
- ↑ 4,0 4,1 4,2 4,3 4,4 4,5 А. Ю. Морозов. Струн теория – А. М. Прохоров (toim). Физическая энциклопедия, М., Советская энциклопедия: 1988, kd 5.
- ↑ Scherk J., Schwarz J. H.. Dual models for non-hadrons. – Nucl.Phys, 1974, kd 81, nr 1, lk 118–144
- ↑ 6,0 6,1 Морозов А. Ю. Теория струн – что это такое? – УФН, 1992, kd 162, nr 8, lk 83–175.
- ↑ Veneziano G. Nuovo Cim., 1968, 57A, 190 (ka M. Suzuki avaldamata töö, 1968).
- ↑ Б. Паркер. Мечта Эйнштейна. В поисках единой теории строения Вселенной, М., Амфора, 2000, ISBN 5-8301-0198-Х.
- ↑ Polchinski, Joseph (1998). String Theory, Cambridge University Press.
- ↑ Каку, Мичио. Введение в теорию суперструн, пер. с англ. Г.Э. Арутюнова, А.Д. Попова, С.В. Чудова; под ред. И. Я. Арефьевой, Мир 1999, ISBN 5-03-002518-9.
- ↑ Yau S., Witten E. Symposium on Anomalies, Geometry and Topology, 1985, WS, Singapur; Witten E. jt. – Nukl.Phys., 1985, B261, 678; 1986, B274, 286.
- ↑ Peter Woit. Теория струн: оценка.
- ↑ Lisa Randall. Extra Dimensions and Warped Geometries, Science, 2002, kd 296, nr 5572, lk 1422–1427.
- ↑ Võrdluseks: aatomi diameetrisse mahub umbes sama palju stringe kui aatomeid sirglõigule Maalt Proxima Centaurini.
- ↑ Струна. – А. М. Прохоров (toim). Физическая энциклопедия, М., Советская энциклопедия: 1988, kd 5.
- ↑ 16,0 16,1 Бухбиндер И. Л. "Теория струн и объединение фундаментальных взаимодействий". – Соросовский образовательный журнал, 2001, nr 7, lk 99.
- ↑ Барбашов, Б. М., Нестеренко, В. В. Суперструны – новый подход к единой теории фундаментальных взаимодействий. – Успехи физических наук, kd 150, nr 4, 1986, lk 489–524.
- ↑ Новая картина струнной теории, Перевод "Официального Сайта Теории Суперструн"
- ↑ 19,0 19,1 19,2 19,3 19,4 Грин, Брайан. "The Elegant Universe. Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory Элегантная Вселенная. Суперструны, скрытые размерности и поиски окончательной теории", Пер. с англ. Под ред. В. О. Малышенко. Изд. 3-е, Едиториал УРСС 2007, ISBN 5-484-00784-4
- ↑ Green M., Schwarz J. Phys. Lett. 1984, 149B, 117.
- ↑ Polyakov A.M. Phys. Lett. 1981, 103B, 207, 211.
- ↑ Belavin A.A., Polyakov A.M., Zamolodchikov A.B. Nucl. Phys. 1984, B241, 333.
- ↑ S. James Gates, Jr., Ph.D., Superstring Theory: The DNA of Reality «Lecture 23 – Can I Have that Extra Dimension in the Window?», 0:04:54, 0:21:00.
- ↑ M. J. Duff, James T. Liu, R. Minasian. Eleven Dimensional Origin of String/String Duality: A One Loop Test Center for Theoretical Physics, Department of Physics, Texas A&M University.
- ↑ Новая картина струнной теории, Перевод "Официального Сайта Теории Суперструн"
- ↑ Иванов, Игорь. Дифракция в физике элементарных частиц: рассказ первый. Дневник в рамках проекта «Элементы», 15.09.2006.
- ↑ G. F. Chew, S. C. Frautschi. Phys. Rev. Letters, 8, 41 (1962); S. C. Frautschi. "Regge Poles and S-Matrix Theory", (W. A. Benjamin, New York, 1968).
- ↑ 28,0 28,1 Левин, А. Струнный концерт для Вселенной. – Популярная механика, märts 2006.
- ↑ Shapiro J. Phys. Rev., 1971, 33В, 361. Virasoro M. Phys. Rev., 1969, 177, 2309. Ramond P. Phys. Rev., 1971, D3, 2415. Neveu A., Schwarz J. Nucl. Phys., 1971, B31, 86. Lovelace C. Phys. Rev., 1974, 34B, 500.
- ↑ Ю. П. Рыбаков. Тахион. – А. М. Прохоров (toim). Физическая энциклопедия, М., Советская энциклопедия: 1988, kd 5.
- ↑ Wess J., Zumino B. Nucl.Phys. 1974, B70, 39.
- ↑ Gliozzi F., Sherk J., Ollive D. Nucl.Phys. 1977, B122, 253.
- ↑ Green M., Schwarz J. Nucl.Phys. 1981, B81, 253. Green M., Schwarz J. Phys. Lett. 1984, 149B, 117.
- ↑ В. И. Огиевецкий. Гравитон. – А. М. Прохоров (toim). Физическая энциклопедия, М., Советская энциклопедия: 1988, kd 1.
- ↑ Франке В.А. Учебный план физического факультета СПбГУ, Санкт-Петербургский государственный университет.
- ↑ Vladimir G. Ivancevic, Tijana T. Ivancevic. "Applied Differential Geometry: A Modern Introduction", World Scientific Publishing Company, 2007, lk 41. ISBN 978-981-270-614-0.
- ↑ Sel teemal avaldatud artiklite statistika aastate kaupa: AdS/CFT correspondence on arxiv.org.
- ↑ S. Kachru, R. Kallosh, A. Linde and S. P. Trivedi. de Sitter Vacua in String Theory. "Phys.Rev." D68:046005, 2003.
- ↑ M. Douglas. The statistics of string / M theory vacua. JHEP 0305, 46 (2003).
- ↑ S. Ashok, M. Douglas. Counting flux vacua. JHEP 0401, 060 (2004).