Autosimilarité


L'autosimilarité est le caractère d'un objet dans lequel on peut trouver des similarités en l'observant à différentes échelles.
Définition et précision sur le concept
[modifier | modifier le code]
Une définition simplifiée, faisant appel à l'intuition, pourrait être : un objet autosimilaire est un objet qui conserve sa forme, quelle que soit l'échelle à laquelle on l'observe. La définition mathématique, formelle et rigoureuse, dépend du contexte.
L’expression autosimilaire n’est pas encore reconnue par l’Académie française. Elle provient, en effet, d’une traduction de l'adjectif anglais self-similar, et les traductions ne sont pas encore clairement fixées à ce sujet. L'anglais similar se traduit d'ailleurs par semblable.
Les objets autosimilaires ne sont pas à confondre avec les fractales : la droite, le plan, l'espace sont autosimilaires sans pour autant être fractals.
On peut distinguer deux types d'autosimilitude.
Autosimilitude parfaite
[modifier | modifier le code]On dit qu'un compact K de Rn est autosimilaire s'il existe une famille finie de p fonctions contractantes fi de Rn telle que K soit la réunion des fi(K)[1]. Cette définition trouve son intérêt au moins dans le domaine de système de fonctions itérées puisque tout attracteur d'une famille de contractions est autosimilaire.
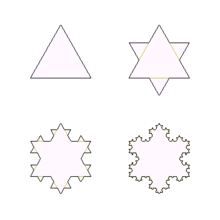
Autosimilitude approchée ou statistique
[modifier | modifier le code]
Cette expression est ambiguë car l'autosimilitude approchée peut désigner une fractale, comme l’ensemble de Mandelbrot, dans laquelle des motifs et des structures générales se répètent à toutes les échelles.
L’autosimilitude statistique désigne généralement une propriété d’objet concret qui semble se comporter comme des objets possédant une autosimilitude approchée à nos échelles d’observation humaine. En effet, à partir de l'image d’un nuage, par exemple, il sera difficile de dire à quelle échelle a été prise la photographie. De même, la côte de Bretagne présente des similitudes, que l’observation se fasse d’avion ou à la loupe. Les courbes représentant le cours d’actions en bourse peuvent également être vues comme un objet autosimilaire, pour les mêmes raisons que les autres exemples.
Toutefois, ce dernier type d’objet autosimilaire ne correspond pas à la vision mathématique car, bien que l’on retrouve, en effet, des structures générales identiques à nos échelles, à l’échelle nanoscopique, les structures intimes de la matière font que l’autosimilitude disparaît.
Bibliographie
[modifier | modifier le code]- M. Laguës et A. Lesne, Invariances d'échelle : Des changements d'états à la turbulence, Paris, Belin, , 367 p. (ISBN 978-2-7011-4859-5)
- Benoît Mandelbrot, Fractales, hasard et finances, Paris, Gallimard, coll. « Champs sciences », , 246 p. (ISBN 2-08-122510-7)
Notes et références
[modifier | modifier le code]Notes
[modifier | modifier le code]Références
[modifier | modifier le code]- (en) John Hutchinson, « Fractals and self similarity », Indiana University Mathematical Journal, (lire en ligne)