Prévision d'ensembles

La prévision d'ensembles est une méthode de prévision numérique du temps utilisé pour tenter de générer un échantillon représentatif des états futurs possibles d'un système dynamique. En effet, ni les observations, ni l'analyse, ni le modèle de prévision ne sont parfaits et la dynamique atmosphérique est très sensible, dans certaines conditions, à la moindre fluctuation.

C'est une forme de méthode de Monte Carlo : plusieurs prédictions numériques sont réalisées à l'aide de conditions initiales légèrement différentes mais plausibles étant donné les limites de résolution des observations et des équations. Dans chaque cas, l'analyse est délibérément rendue légèrement différente des autres membres de l'ensemble, à l'intérieur des incertitudes intrinsèques de mesure ou d'analyse. Les scénarios plus ou moins divergents des prévisions offertes par les membres de l'ensemble permettent de quantifier la prévisibilité de l'atmosphère et d'offrir une marge d'erreur statistique sur la prévision.

Dans les premières décennies d'existence de la prévision numérique du temps, les services météorologiques nationaux ne pouvaient faire tourner qu'un seul modèle à la plus haute résolution permise par les contraintes informatiques, et adopter cette prévision telle quelle. Cette approche suppose implicitement que si les conditions initiales étaient connues parfaitement, et que le modèle lui-même était parfait, la prévision qui s'ensuivrait simulerait parfaitement le comportement futur de l'atmosphère. On qualifie cette approche de déterministe.

Edward Lorenz démontra en 1963 que les prévisions déterministes à plus de deux semaines avec un quelconque degré de confiance sont impossibles. Ceci est dû à la nature chaotique des équations de la dynamique des fluides impliquées^[1]. Par ailleurs, les réseaux d'observation existants sont limités et leur résolution temporelle variable (par exemple très faible sur les océans) ce qui introduit une incertitude dans l'état initial de l'atmosphère. Même si les équations Liouville permettent de limiter l'incertitude d'initialisation, elles sont trop complexes pour fonctionner en temps réel, même avec l'utilisation de superordinateurs^[2]. Ces incertitudes limitent le modèle de prévision à environ six jours dans le futur^[3].

Reconnaissant en 1969 que l'atmosphère ne pouvait être complètement décrite du fait de ces incertitudes, Edward S. Epstein proposa un modèle dynamique stochastique produisant des moyennes et des écarts pour l'état de l'atmosphère^[4]. Bien que ces simulations de Monte Carlo démontrèrent une certaine aptitude, Cecil Leith démontra en 1974 qu'elles ne produisaient une prévision adéquate seulement lorsque la distribution des échantillons était représentatif de la loi de probabilité dans l'atmosphère^[5]. Il a fallu attendre 1992 pour que des prévisions d'ensembles soient introduites par le CEPMMT et le NCEP.

Par la suite, un intérêt marqué s'est développé dans la communauté de chercheurs en prévision d'ensemble envers les ensembles multi-modèles (c’est-à-dire combinant des modèles de différentes conceptions) et l'agrégation de SPE de différents pays, menant à la formation de super-ensembles. En 2006, deux efforts concrets existaient en ce sens, soit le Système nord-américain de prévision d'ensembles (Canada, États-Unis, Mexique) et le "THORPEX Interactive Grand Global Ensemble", ou TIGGE (sous la coordination de l'Organisation météorologique mondiale).

Aujourd'hui, les prévisions d'ensembles sont produites par la plupart des services météorologiques nationaux, dans les mêmes installations informatiques que les prévisions météorologiques opérationnelles déterministes, et combinés dans des super-ensembles. Parmi ces centres, les plus importants sont : le National Centers for Environmental Prediction (NCEP) des États-Unis, le Centre européen pour les prévisions météorologiques à moyen terme (CEPMMT), le Centre de recherche en prévision numérique canadien et Météo-France. Nombres d'universités et de chercheurs travaillent également au développement des modèles.

Les modèles stochastiques de prévision numérique du temps, ou d'ensembles, sont utilisés pour tenir compte de l'incertitude de l'atmosphère. Ils impliquent de multiples prévisions créées en utilisant différentes paramétrisations physiques ou conditions initiales^[2]. L'ensemble de prévisions peut ainsi utiliser des modèles de prévision différents pour les différents membres ou des variations différentes d'un seul modèle de prévision^[6].

Les multiples simulations sont effectuées pour tenir compte des deux sources habituelles d'incertitude dans les modèles de prévision : les erreurs introduites par l'utilisation de conditions initiales imparfaites, amplifiée par la nature chaotique des équations d'évolution du système dynamique sensible aux conditions initiales, les erreurs introduites en raison d'imperfections dans la formulation du modèle, tels que les méthodes mathématiques tronquées pour résoudre les équations^[6]. Idéalement, l'état du système dynamique devrait se retrouver dans la dispersion des trajectoires de l'ensemble prévu et la dispersion de celles-ci devrait être lié à l'incertitude de la prévision.

Plusieurs méthodes permettent de créer des ensembles, chacune impliquant des éléments d’incertitude, soit dans les données ou dans le modèle de prévision numérique. Chacune des prévisions dans un ensemble (appelée « membre » de l’ensemble) utilise un ou plusieurs aspects de cette incertitude. Les méthodes possibles pour capturer l’incertitude inhérente dans la prévision incluent^[6] :

• Perturbation des conditions initiales utilisées par le modèle de prévision ;
• Perturbation du modèle, par des modifications dans :
  • la formulation de la dynamique (ex. différents types de coordonnées verticales) ;
  • les méthodes numériques (ex. méthodes de calcul différentes, représentation par points de grille versus spectrale) ;
  • les paramétrisations physiques (ex. méthode différentes de générer des précipitations à l'échelle synoptique de la maille ou sous-maille pour celles convectives) ;
  • la résolution horizontale ou verticale.

• Perturbations des conditions aux limites, celles-ci étant les bordures du domaine où se fait le calcul (continent, hémisphère ou Terre entière) :
  • conditions aux limites en surface (ex. température de surface de la mer ou humidité du sol) ;
  • conditions aux limites latérales (ex. perturber les conditions fournies par une prévision d’ensemble faite pour un domaine plus grand).

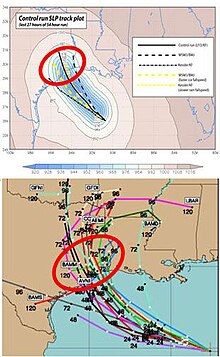
La prévision d'ensemble est ainsi généralement évaluée en termes de la moyenne des prévisions individuelles concernant une variable de prévision et le degré d'accord entre les différentes prévisions au sein du système d'ensembles. La propagation des membres de l'ensemble est diagnostiquée grâce à des outils tels que les diagrammes spaghetti qui montrent la trajectoire de chaque membre sur les cartes à des temps spécifiques dans le futur. Un autre outil utilisé est le météogramme qui montre la dispersion dans des prévisions d'une quantité pour un emplacement spécifique. Malgré tout, il arrive souvent que le déplacement des systèmes météorologiques ne tombent pas à l'intérieur de l'enveloppe des trajectoires prévues et ce problème s'accentue avec le temps de prévision au-delà de 10 jours^[7]

Lorsque la dispersion des résultats des ensembles est faible et les solutions sont cohérentes au sein de plusieurs simulations du modèle, les prévisionnistes sont plus confiants dans la moyenne de l'ensemble et les prévisions en général^[8]. Une corrélation de moins de 0,6 de la dispersion est généralement perçue comme un ensemble qui offre une bonne prédictibilité^[9]. La fiabilité varie considérablement en fonction de facteurs tels que le modèle de prévision et la région pour laquelle la prévision est faite.

Idéalement, la fréquence relative des événements de l'ensemble peut être directement utilisée pour estimer la probabilité d'un événement de temps donné. Par exemple, si 30 des 50 membres ont indiqué plus de 1 cm de précipitations pendant les 24 heures suivantes, la probabilité de dépasser ce seuil peut être estimée à 60 %. La prévision sera considérée fiable si dans les situations similaires dans le passé, 60 % des cas où 1 cm était prévue il y a eu en fait 1 cm ou plus. Dans la pratique, cette façon d'évaluer la probabilité est très peu fiable.

Une autre propriété souhaitable des prévisions d'ensemble est la netteté. A condition que l'ensemble soit fiable, plus une prévision d'ensembles diffère de la moyenne climatologique, plus utile seront les prévisions. En effet, elles montreront que le système se déplace de façon indépendante de la circulation atmosphérique journalière. Cependant, les prévisions nettes qui ne sont pas accompagnés d'une grande fiabilité ne seront généralement pas utile.

Les prévisions d'ensembles ont plusieurs avantages^[6] :

• L’incertitude sur les conditions initiales peut être prise en compte en déterminant les erreurs possibles qui grossissent rapidement pour la prévision subséquente du modèle et en les réduisant à une perturbation raisonnable des conditions initiales ;
• La prévisibilité peut être estimée par le taux de croissance de la dispersion des prévisions membres de l’ensemble. Elle peut varier selon la taille de l’ensemble et le choix des perturbations des conditions initiales ;
• Plusieurs méthodes numériques (analyse spectrale ou sur grille fixe/variable de l'atmosphère) ;
• Plusieurs combinaisons de paramétrisations physiques (par exemple, on peut utiliser deux types de paramétrisation de la convection atmosphérique pour combiner les points forts de chacun).

Les inconvénients sont :

• Les résultats donnent une idée de la variabilité de l'évolution des systèmes météorologiques mais pas celui qui est le cas le plus probable ;
• Le scénario moyen de tous les membres n'est pas nécessairement celui qui se produira.

v · m Modèles atmosphériques, océaniques et climatiques
Types	Modèle de circulation générale Modèle de circulation générale océanique Modèle climatique Modélisation de la dispersion atmosphérique Prévision des cyclones tropicaux Prévision numérique du temps Prévision d'ensembles Réanalyse météorologique Reprévision météorologique
Par pays	Canada GEMLAM GLOBAL États-Unis GFS NAM WRF Europe IFS (modèle du CEPMMT) Climateprediction.net Réanalyse du CEPMMT
Glossaire de la météorologie

• Portail de la météorologie
• Portail des mathématiques