פונקציית דלתא של דיראק

פונקציית הדלתא של דיראק, המסומנת ${\displaystyle \ \delta (x)}$, היא פונקציה מוכללת שימושית בפיזיקה, בהנדסה ובהסתברות. למרות שמה, היא אינה פונקציה במובן המקובל. הגדרתה היא על פי תכונות של האינטגרל המסוים שלה: לכל A ו-B חיוביים מתקיים

${\displaystyle \int _{A}^{B}\delta (x)dx=\int _{-A}^{-B}\delta (x)dx=0}$

${\displaystyle \int _{-A}^{B}\delta (x)dx=1}$

התחום של פונקציית דלתא הוא קבוצת המספרים הממשיים. מהתכונה הראשונה ניתן להסיק שהערך של ${\displaystyle \ \delta (x)}$ הוא אפס לכל x פרט ל-x=0. כדי לקיים את התכונה השנייה, הערך ב-x=0 לא יכול להיות מספר סופי, ולכן הטווח שלה אינו מוכל בקבוצת המספרים הממשיים. אולם ערכי הפונקציה אינם מעניינים בפני עצמם, אלא האינטגרלים שלה.

פונקציית הדלתא של דיראק, שהיא הכללה של פונקציית הדלתא של קרונקר, נוסחה על ידי הפיזיקאי פול דיראק. ניתן להגדיר אותה במספר דרכים, למשל כגבול חלש של סדרה של פונקציות שהשטח מתחת לגרף של כל אחת מהן הוא 1, בעוד שהתחום בו הן אינן מתאפסות זהותית הוא קטע הולך וקטן סביב x=0.

לרוב, פונקציית דלתא מוגדרת באמצעות התכונה הבאה

${\displaystyle \int _{-\infty }^{\infty }f(x)\,\delta (x)\,dx=f(0)}$

לכל פונקציה רציפה f. אפשר לחשוב על פונקציית דלתא, מבחינה אינטואיטיבית, כפונקציה שמקבלת את הערך 0 בכל נקודה שאיננה אפס ואת "הערך אינסוף" (או ליתר דיוק ערך אינסופי כלשהו) בנקודת האפס, כך שהאינטגרל המוכלל של הפונקציה על הישר הממשי הוא 1. זו אינה פונקציה במובן המקובל, אבל ההצגה הזו מאפשרת להבין חלק מתכונות הפונקציה.

באופן כללי יותר אפשר לרשום:

${\displaystyle \forall f\in C[-\infty ,\infty ]\ :\ \int _{-\infty }^{\infty }f(x)\,\delta (x-x_{0})\,dx=f(x_{0})}$

ניתן לראות את פונקציית דלתא כפונקציית צפיפות של התפלגות בדידה בעלת פונקציית הסתברות המקבלת 0 לפני ערך מסוים ו-1 אחריו, כלומר:

${\displaystyle H(x)=\left\{{\begin{matrix}0&:&x<0\\1&:&x>0\end{matrix}}\right.}$

לפונקציית הסתברות כזו קוראים פונקציית הביסייד (פונקציית מדרגה), והיא פונקציה קדומה של פונקציית דלתא. לכן באופן לא-פורמלי אפשר לתאר את פונקציית דלתא כ"נגזרת" של פונקציית הביסייד (למרות שלפונקציה זו יש נקודת אי-רציפות בה לא ניתן להגדיר נגזרת), כלומר:

${\displaystyle \ dH(x)=\delta (x)\ dx}$

אינטואיטיבית, סביב כל x שונה מ-0 פונקציית הביסייד היא קבועה, ולכן נגזרתה אפס, אך עבור x=0 יש בפונקציית הביסייד קפיצה עם "שיפוע" אינסופי ולכן נגזרת אינסופית בנקודה זו. תכונות אלה מתאימות לתיאור האינטואיטיבי של פונקציית דלתא.

אין פונקציה שמקיימת את התכונות האלו אך אפשר להגדיר את "פונקציית דלתא" באמצעות שימושים במושגים מתמטיים אחרים: פונקציונל או מידה של אינטגרל לבג.

כפונקציונל, אפשר להגדיר את פונקציית דלתא באופן הבא:

${\displaystyle \ \forall \ \phi :\mathbb {R} \to \mathbb {R} \ :\ \delta [\phi ]=\phi (0)\,}$

זהו פונקציונל לגיטימי הפועל על מרחב הפונקציות הממשיות. פונקציונל זה אמנם חסום בנורמת הסופרמום אך הוא אינו חסום (ולכן גם לא רציף) במרחב הילברט ${\displaystyle \ L_{2}}$. יתרה מכך, הוא אינו מוגדר היטב באותו מרחב, כיוון ששם שתי פונקציות נחשבות לשוות אם הן נבדלות לכל היותר על קבוצת נקודות בעלת מידה אפס, ולכן אין משמעות לערך הפונקציה בנקודה ספציפית. למרות זאת, מאחר שלפי משפט ההצגה של ריס אפשר לרשום כל פונקציונל ליניארי חסום כמכפלה פנימית (ובמרחב ${\displaystyle \ L_{2}}$ כאינטגרל) רושמים גם את הפונקציונל הזה כאינטגרל. זהו רק סימון נוח ואין למעשה שום פונקציה שמקיימת את השוויון.

אפשר גם להתייחס לפונקציית דלתא כאל מידה באופן הבא:

• ${\displaystyle \ \delta (A)=1}$ אם ${\displaystyle 0\in A}$.
• ${\displaystyle \ \delta (A)=0}$ אחרת.

על ידי שימוש במידה זו, אפשר לרשום אינטגרל לבג ולקבל:

${\displaystyle \forall f\in C[-\infty ,\infty ]\ :\ \int _{-\infty }^{\infty }f(x)\,\delta \{dx\}=f(0)}$

רישום זה מבלבל ועדיף עליו הסימון:

${\displaystyle \forall f\in C[-\infty ,\infty ]\ :\ \int _{-\infty }^{\infty }f(x)\,dH(x)=f(0)}$

כאשר H היא פונקציית הביסייד. את הרישום האחרון אפשר להצדיק במסגרת התורה של אנליזה פונקציונלית ואינטגרלים ספקטרליים.

את פונקציית דלתא אפשר לתאר גם כגבול של סדרת פונקציות. כל פונקציה בסדרה נהיית צרה יותר אך גבוהה יותר יחסית לקודמתה, והשטח שמתחת לגרף שלה נשאר קבוע - 1.

באופן פורמלי, סדרת פונקציות ${\displaystyle \ \left\{\delta _{n}(x)\right\}_{n=1}^{\infty }}$ תקרא "סדרת דלתא" אם:

1. ${\displaystyle \ \forall n\in \mathbb {N} \ :\ \int _{-\infty }^{\infty }{\delta _{n}(x)dx}=1}$, דרישה זאת קובעת שלכל הפונקציות בסדרה יש משקל (שטח מתחת לעקומה) של 1.
2. לכל ${\displaystyle \ \varepsilon >0}$ קיים ${\displaystyle \ N_{0}}$ מספיק גדול כך ש ${\displaystyle \ \forall n>N_{0}\ :\ \forall |x|\geq \varepsilon \ :\ \delta _{n}(x)=0}$.

דוגמאות לסדרות של פונקציות שמקיימות את הנדרש: פונקציית המלבן, גאוסיאן, לורנציאן.

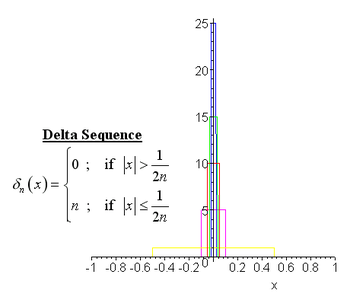
למשל נסתכל בסדרה הבאה של פונקציות המלבן:

${\displaystyle \delta _{n}(x)=\left\{{\begin{matrix}0&:&|x|>{\frac {1}{2n}}\\n&:&|x|<{\frac {1}{2n}}\end{matrix}}\right.}$

זוהי סדרה של פונקציות שהגרפים שלהן הם מלבנים, או פונקציות מציינות על הקטע ${\displaystyle \ \left[-1/(2n),+1/(2n)\right]}$ המוכפלות ב-n, כמתואר בתרשים.

נראה שזוהי סדרת דלתא:

1. שטח: כל מלבן הוא ברוחב ${\displaystyle \ 1/n}$ ובגובה n ולכן השטח שלו שווה ל-1.
2. עבור כל ${\displaystyle \varepsilon }$ שנקבל, ${\displaystyle N_{0}=\left\lceil {\frac {1}{2\varepsilon }}\right\rceil }$ מקיים את הדרישה השנייה.

• ${\displaystyle \ \delta (t)=\delta (-t)}$ (זוגיות)
• ${\displaystyle \ \delta (at)={\frac {1}{|a|}}\delta (t)}$ (שינוי קנה מידה)
• ${\displaystyle x(t)\delta (t-t_{0})=x(t_{0})\delta (t-t_{0})}$
• ${\displaystyle \int _{-\infty }^{\infty }x(t)\delta (t-t_{0})\,dt=x(t_{0})}$
• ${\displaystyle \int _{a}^{b}x(t)\delta (t-t_{0})\,dt={\begin{cases}x(t_{0})&,t_{0}\in [a,b]\\0&,t_{0}\notin [a,b]\end{cases}}}$
• ${\displaystyle \{x(t)\}*\{\delta (t-t_{0})\}=x(t-t_{0})}$ (קונבולוציה)
• התמרת פורייה של הפונקציה היא הפונקציה הקבועה ${\displaystyle f(x)=1}$, ומכאן ההתמרה ההפוכה: :${\displaystyle \delta (x)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }1\cdot e^{ikx}\,dk}$
• ${\displaystyle \delta ^{'}(x)f(x)=\delta ^{'}(t)f(0)-\delta (t)f^{'}(0)}$

באמצעות החלפת משתנים באינטגרציה ותכונת הזוגיות אפשר להוכיח ש- ${\displaystyle \ \delta (ax)={\frac {1}{|a|}}\delta (x)}$.

הוכחה: נניח ש-a חיובי (אם a שלילי, נשתמש בתכונת הזוגיות ונעבוד עם ${\displaystyle -a}$ כארגומנט הפונקציה). כעת,

${\displaystyle \int _{-\infty }^{\infty }f(x)\delta (ax)dx={\frac {1}{|a|}}\int _{-\infty }^{\infty }f(y/|a|)\delta (y)dy={\frac {1}{|a|}}f(0)}$ כאשר ביצענו את החלפת המשתנים ${\displaystyle y=ax}$. ‏ ${\displaystyle \ \blacksquare }$

באופן כללי יותר מתקיים ש-

${\displaystyle \delta (g(x))=\sum _{i}{\frac {\delta (x-x_{i})}{|g'(x_{i})|}}}$

כלומר, תחת האינטגרל מתקיים:

${\displaystyle \int _{-\infty }^{\infty }f(x)\,\delta (g(x))\,dx=\sum _{i}{\frac {f(x_{i})}{|g'(x_{i})|}}}$

כאשר x_i הם השורשים של g, כלומר: ${\displaystyle \ g(x_{i})=0}$.

הוכחה: מאחר שבכל קטע I בו ${\displaystyle g(x)\neq 0}$ האינטגרל ${\displaystyle \int _{I}f(x)\delta (g(x))dx=0}$ אפשר להפריד את האינטגרל לסכום של אינטגרלים על קטעים קטנים כרצוננו סביב שורשי g, כלומר:

${\displaystyle \int _{-\infty }^{\infty }f(x)\delta (g(x))dx=\sum _{i}\int _{x_{i}-\varepsilon }^{x_{i}+\varepsilon }f(x)\delta (g(x))dx}$

מאחר שהקטעים קטנים כרצוננו, אפשר בכל קטע לקרב את g על ידי קירוב ליניארי: ${\displaystyle g(x)=g'(x_{i})(x-x_{i})}$. נציב זאת באינטגרל ונשתמש בתכונה ${\displaystyle \ \delta (ax)={\frac {1}{|a|}}\delta (x)}$, נקבל

${\displaystyle \sum _{i}\int _{x_{i}-\varepsilon }^{x_{i}+\varepsilon }f(x)\delta (g(x))dx=\sum _{i}\int _{x_{i}-\varepsilon }^{x_{i}+\varepsilon }f(x)\delta {\Big (}g'(x_{i})(x-x_{i}){\Big )}dx=\sum _{i}{\frac {1}{|g'(x_{i})|}}\int _{x_{i}-\varepsilon }^{x_{i}+\varepsilon }f(x)\delta (x-x_{i})dx=\sum _{i}{\frac {f(x_{i})}{|g'(x_{i})|}}}$

כנדרש. ${\displaystyle \ \blacksquare }$

עבור פונקציית מבחן גזירה, אפשר לחשב את הנגזרת של פונקציית דלתא באמצעות אינטגרציה בחלקים ולקבל ש : ${\displaystyle \delta '[\phi ]=-\phi '(0)\,}$.

• מכאן נובע: ${\displaystyle \delta '(x)=-{\frac {\delta (x)}{x}}}$.
• כמו כן: ${\displaystyle \delta ^{(n)}[\phi ]=(-1)^{n}\phi ^{(n)}(0)\,}$.

• בפיזיקה, פונקציית דלתא היא התיאור המתמטי (פונקציית ההתפלגות) של מטען חשמלי נקודתי או מסה נקודתית. הפונקציה מוגדרת עבור וקטור מיקום ${\displaystyle \mathbf {x} }$ כ-${\displaystyle \delta (\mathbf {x} )=\delta (x_{1})\delta (x_{2})\cdots \delta (x_{n})}$‏.
• בהנדסת חשמל, עיבוד אותות ואנליזת פורייה, פונקציית דלתא (הנקראת גם הלם - באנגלית impulse) משמשת לביצוע מניפולציות של התמרת פורייה, ולניתוח אותות ומערכות. מערכת ליניארית בלתי תלויה בזמן ניתנת לאפיון מלא על ידי התגובה שלה להלם.
• בהסתברות, פונקציית דלתא היא פונקציית צפיפות המתאימה לפונקציית ההסתברות של התפלגות מנוונת. התפלגות בדידה לא-מנוונת ניתנת לתיאור על ידי סכום משוקלל של פונקציות דלתא מוזזות.
• במכניקת הקוונטים משתמשים לעיתים בפונקציות דלתא כבסיס למרחב המקום או התנע. הפונקציה הדואלית לפונקציית דלתא מוזזת היא גל מישורי: ${\displaystyle \ e^{ipx/\hbar }}$.
• בתורת שטורם-ליוביל המשמשת לפתרון משוואות דיפרנציאליות, פונקציית דלתא מספקת את אחת משתי ההגדרות לפונקציית גרין, ובכך מאפשרת לפתור באופן שיטתי משוואות דיפרנציאליות אי הומוגניות.

• פונקציית מדרגה
• הדלתא של קרונקר
• תורת שטורם-ליוביל
• מסרק דיראק

מיזמי קרן ויקימדיה
ספר לימוד בוויקיספר: תורת הבקרה/פונקציית הלם
תמונות ומדיה בוויקישיתוף: פונקציית דלתא של דיראק

• פונקציית דלתא באתר wolfram
• פונקציית דלתא מרחבית בבלוג "רשימות בפיזיקה עיונית"
• פונקציית דלתא של דיראק, באתר MathWorld (באנגלית)