У этого термина существуют и другие значения, см.
Бета .
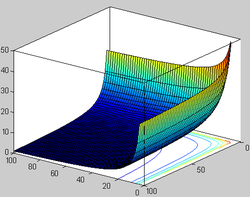
График бета-функции при вещественных аргументах В математике бета-функцией ( B {\displaystyle \mathrm {B} } интегралом Эйлера I рода) называется следующая специальная функция от двух комплексных переменных:
B ( x , y ) = ∫ 0 1 t x − 1 ( 1 − t ) y − 1 d t , {\displaystyle \mathrm {B} (x,y)=\int \limits _{0}^{1}t^{x-1}(1-t)^{y-1}\,dt,} определённая при Re x > 0 {\displaystyle \operatorname {Re} x>0} Re y > 0 {\displaystyle \operatorname {Re} y>0}
Бета-функция была изучена Эйлером , Лежандром [когда? , а название ей дал Жак Бине .
Бета-функция симметрична относительно перестановки переменных, то есть
B ( x , y ) = B ( y , x ) . {\displaystyle \mathrm {B} (x,y)=\operatorname {\mathrm {B} } (y,x).} Бета-функцию можно выразить через другие функции:
B ( x , y ) = Γ ( x ) Γ ( y ) Γ ( x + y ) , {\displaystyle \mathrm {B} (x,y)={\frac {\Gamma (x)\Gamma (y)}{\Gamma (x+y)}},} где Γ ( x ) {\displaystyle \Gamma (x)} Гамма-функция ;
B ( x , y ) = 2 ∫ 0 π / 2 sin 2 x − 1 θ cos 2 y − 1 θ d θ , Re x > 0 , Re y > 0 ; {\displaystyle \mathrm {B} (x,y)=2\int \limits _{0}^{\pi /2}\sin ^{2x-1}\theta \cos ^{2y-1}\theta \,d\theta ,\quad \operatorname {Re} x>0,\ \operatorname {Re} y>0;} B ( x , y ) = ∫ 0 ∞ t x − 1 ( 1 + t ) x + y d t , Re x > 0 , Re y > 0 ; {\displaystyle \mathrm {B} (x,y)=\int \limits _{0}^{\infty }{\frac {t^{x-1}}{(1+t)^{x+y}}}\,dt,\quad \operatorname {Re} x>0,\ \operatorname {Re} y>0;} B ( x , y ) = 1 y ∑ n = 0 ∞ ( − 1 ) n ( y ) n + 1 n ! ( x + n ) , {\displaystyle \mathrm {B} (x,y)={\frac {1}{y}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(y)_{n+1}}{n!(x+n)}},} где ( x ) n {\displaystyle (x)_{n}} нисходящий факториал , равный x ⋅ ( x − 1 ) ⋅ ( x − 2 ) ⋅ … ⋅ ( x − n + 1 ) {\displaystyle x\cdot (x-1)\cdot (x-2)\cdot \ldots \cdot (x-n+1)}
Подобно тому как гамма-функция для целых чисел является обобщением факториала , бета-функция является обобщением биномиальных коэффициентов с немного изменёнными параметрами:
( n k ) = 1 ( n + 1 ) B ( n − k + 1 , k + 1 ) . {\displaystyle {\binom {n}{k}}={\frac {1}{(n+1)\mathrm {B} (n-k+1,k+1)}}.} Бета-функция удовлетворяет двумерному разностному уравнению :
B ( x , y ) − B ( x + 1 , y ) − B ( x , y + 1 ) = 0. {\displaystyle \mathrm {B} (x,y)-\mathrm {B} (x+1,y)-\mathrm {B} (x,y+1)=0.} Частные производные у бета-функции следующие:
∂ ∂ x B ( x , y ) = B ( x , y ) ( Γ ′ ( x ) Γ ( x ) − Γ ′ ( x + y ) Γ ( x + y ) ) = B ( x , y ) ( ψ ( x ) − ψ ( x + y ) ) , {\displaystyle {\frac {\partial }{\partial x}}\mathrm {B} (x,y)=\mathrm {B} (x,y)\left({\frac {\Gamma '(x)}{\Gamma (x)}}-{\frac {\Gamma '(x+y)}{\Gamma (x+y)}}\right)=\mathrm {B} (x,y){\big (}\psi (x)-\psi (x+y){\big )},} ∂ ∂ y B ( x , y ) = B ( x , y ) ( Γ ′ ( y ) Γ ( y ) − Γ ′ ( x + y ) Γ ( x + y ) ) = B ( x , y ) ( ψ ( y ) − ψ ( x + y ) ) , {\displaystyle {\frac {\partial }{\partial y}}\mathrm {B} (x,y)=\mathrm {B} (x,y)\left({\frac {\Gamma '(y)}{\Gamma (y)}}-{\frac {\Gamma '(x+y)}{\Gamma (x+y)}}\right)=\mathrm {B} (x,y){\big (}\psi (y)-\psi (x+y){\big )},} где ψ ( x ) {\displaystyle \psi (x)} дигамма-функция .
Неполная бета-функция — это обобщение бета-функции, заменяющее интеграл по отрезку [ 0 , 1 ] {\displaystyle [0,1]}
B x ( a , b ) = ∫ 0 x t a − 1 ( 1 − t ) b − 1 d t . {\displaystyle \mathrm {B} _{x}(a,b)=\int \limits _{0}^{x}t^{a-1}(1-t)^{b-1}\,dt.} При x = 1 {\displaystyle x=1}
Регуляризованная неполная бета-функция определяется через полную и неполную бета-функции:
I x ( a , b ) = B x ( a , b ) B ( a , b ) . {\displaystyle I_{x}(a,b)={\frac {\mathrm {B} _{x}(a,b)}{\mathrm {B} (a,b)}}.} I 0 ( a , b ) = 0 , {\displaystyle I_{0}(a,b)=0,} I 1 ( a , b ) = 1 , {\displaystyle I_{1}(a,b)=1,} I x ( a , b ) = 1 − I 1 − x ( b , a ) , {\displaystyle I_{x}(a,b)=1-I_{1-x}(b,a),} I x ( a + 1 , b ) = I x ( a , b ) − x a ( 1 − x ) b a B ( a , b ) . {\displaystyle I_{x}(a+1,b)=I_{x}(a,b)-{\frac {x^{a}(1-x)^{b}}{aB(a,b)}}.}
Кузнецов Д. С. Специальные функции (1962) — 249 с.


















![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)







