Прямая Симсона

Прямая Симсона — прямая, проходящая через основания перпендикуляров на стороны треугольника из точки на его описанной окружности. Её существование опирается на теорему Симсона.

Основания перпендикуляров, опущенных из произвольной точки ${\displaystyle P}$ описанной окружности треугольника ${\displaystyle ABC}$ на его стороны или их продолжения, лежат на одной прямой. Эта прямая называется прямой Симсона^[1].

Верно и обратное утверждение: если основания перпендикуляров, опущенные из точки ${\displaystyle P}$ на стороны треугольника ${\displaystyle ABC}$ или их продолжения, лежат на одной прямой, то точка ${\displaystyle P}$ лежит на описанной окружности треугольника.

Открытие этой прямой долго приписывалось Роберту Симсону (1687—1768), но в действительности она была открыта лишь в 1797 году шотландским математиком Уильямом Уоллесом. Поэтому, наряду с традиционным названием этой прямой, часто используется исторически более справедливое название: «прямая Уоллеса».^[2]

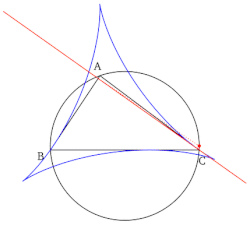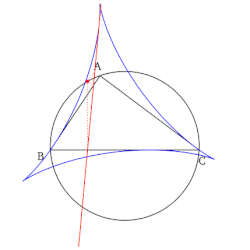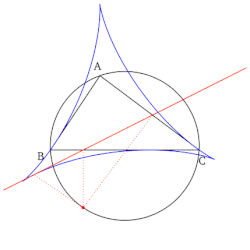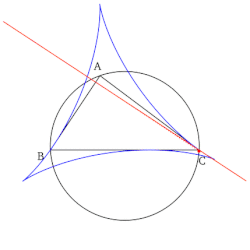
• Пусть ${\displaystyle H}$ — ортоцентр треугольника ${\displaystyle ABC}$. Тогда прямая Симсона произвольной точки ${\displaystyle P}$ на описанной окружности треугольника ${\displaystyle ABC}$ делит отрезок ${\displaystyle PH}$ пополам в точке, лежащей на окружности девяти точек.
• Если P и Q являются точками на описанной окружности, то угол между прямыми Симсона точек P и Q равен половине угла дуги PQ.
  • В частности, если 2 точки на описанной окружности диаметрально противоположны, их прямые Симсона перпендикулярны, и в этом случае точка пересечения 2 перпендикулярных прямых Симсона также лежит на окружности девяти точек. При этом вторые точки пересечения 2 перпендикулярных прямых Симсона с окружностью девяти точек будут концами диаметра последней окружности.
• Для двух данных треугольников с одной и той же описанной окружностью, угол между прямыми Симсона точки P на окружности для обоих треугольников не зависит от P.

• На описанной окружности треугольника ${\displaystyle ABC}$ существуют ровно три точки, таких что их прямая Симсона касается окружности Эйлера треугольника ${\displaystyle ABC}$, причем эти точки образуют правильный треугольник. Стороны этого треугольника параллельны сторонам треугольника Морлея.

• Точки, симметричные точке P на описанной окружности относительно сторон треугольника лежат на одной прямой, проходящей через ортоцентр. Эта прямая (прямая Штейнера) параллельна прямой Симсона и переходит в нее при гомотетии с коэффициентом 1/2

• Точка Фейербаха, то есть точка касания вписанной или вневписанной окружности с окружностью девяти точек, является точкой пересечения двух прямых Симсона, построенных для концов диаметра описанной окружности, проходящего через соответствующий центр вписанной или вневписанной окружности.^[3].
  • В частности, точки Фейербаха могут быть построены без использования соответствующей вписанной или вневписанной окружности и касающейся её окружности Эйлера.

• Огибающая семейства прямых Симсона данного треугольника, есть дельтоида — так называемая дельтоида Штейнера.
  • Якоб Штейнер открыл дельтоиду, как частную гипоциклоиду, которая описывается произвольной фиксированной точкой окружности, которая катится без скольжения внутри окружности в 3 раза большего диаметра. А то, что множество всех возможных линий Симсона, которые могут быть изображены для данного треугольника, имеют огибающую в форме дельтоиды, открыто примерно 100 лет назад и совсем не Штейнером^[4].

• Если ортополюс лежит на прямой Симсона, то его линия ℓ перпендикулярна ей^[5].
• Если прямая ℓ ортополюса пересекает описанную окружность треугольника в двух точках P и Q, то сам ортополюс лежит на пересечении двух прямых Симсона двух последних точек P и Q.^[6]
• Если прямая ℓ ортополюса является прямой Симсона точки P, то точка P называется полюсом прямой Симсона ℓ^[5]

• Помещая треугольник на комплексную плоскость, предположим, что треугольник ABC вписан в единичную окружность и имеет вершины, комплексные координаты которых есть a , b , c , и пусть P с комплексной координатой p является точкой на окружности. Тогда прямая Симсона описывается следующим уравнением на z:^[7]

  ${\displaystyle 2abc{\bar {z}}-2pz+p^{2}+(a+b+c)p-(bc+ca+ab)-{\frac {abc}{p}}=0,}$

где черта сверху указывает на комплексное сопряжение.

• Ни один выпуклый многоугольник, имеющий не менее 5 сторон, не имеет прямой Симсона.^[8]
• Если из данной точки ${\displaystyle P}$ описанной окружности треугольника ${\displaystyle ABC}$ провести прямые под данным ориентированным углом к сторонам, то три полученных точки пересечения будут лежать на одной прямой.
• Прямую Симсона можно определить для любого вписанного ${\displaystyle n}$-угольника по индукции следующим образом: прямой Симсона точки ${\displaystyle P}$ относительно данного ${\displaystyle n}$-угольника назовем прямую, содержащую проекции точки ${\displaystyle P}$ на прямые Симсона всех ${\displaystyle (n-1)}$-угольников, полученных выбрасыванием одной вершины ${\displaystyle n}$-угольника.
• Теорема Сальмона
• Подерный треугольник — треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки на стороны треугольника; в случае когда точка лежит на описанной окружности подерный треугольник вырождается и его вершины лежат на прямой Симсона.
• Пусть ABC — треугольник, и пусть прямая ℓ (зеленая на рисунке) проходит через центр X₃ описанной окружности, а точка P лежит на окружности. Пусть AP, BP, CP пересекают прямую ℓ соответственно в точках A_p, B_p, C_p. Пусть A₀, B₀, C₀ представляют собой проекции точек A_p, B_p, C_p соответственно на прямые BC, CA, AB. Тогда 3 точки A₀, B₀, C₀ коллинеарные точки, то есть лежат на одной прямой. Кроме того, проходящая через них, прямая одновременно проходит через середину отрезка PH, где H является ортоцентром треугольника ABC. Если ℓ проходит через P, то прямая совпадёт с прямой Симсона.^[9][10][11]

• Прямая Симсона точки Штейнера треугольника ${\displaystyle ABC}$ параллельна прямой ${\displaystyle OK}$, а прямая Симсона точки Тарри перпендикулярна прямой ${\displaystyle OK}$, где ${\displaystyle O}$ — центр описанной окружности и ${\displaystyle K}$ — точка пересечения трёх симедиан (точка Лемуана) треугольника ${\displaystyle ABC}$.

• Савелов А. А. Плоские кривые. Систематика, свойства, применения (Справочное руководство) / Под ред. А.П. Нордена. — М.: Физматлит, 1960.
• В. Березин. Дельтоида (рус.) // Квант. — 1977. — № 3. — С. 19.
• E. H. Lockwood. Chapter 8: The Deltoid // A Book of Curves (неопр.). — Cambridge University Press, 1961.
• College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. Nathan Altshiller-Court. Mineola, New York: Dover Publication, Inc., 2012. 292 p.// https://books.google.ru/books?id=VXDWIOvqeaoC&pg=PA291&lpg=PA291&dq=In+geometry,+the+orthopole&source=bl&ots=doCvrYOPtl&sig=ACfU3U1vm-WH5Tr4sGC9cE52DCRf9qBjcA&hl=ru&sa=X&ved=2ahUKEwjq1ZWdiJDqAhWRrIsKHZF7BsYQ6AEwBnoECAoQAQ#v=onepage&q=In%20geometry%2C%20the%20orthopole&f=false.— P. 140-149, 158, 165, 252, 273, 284, 288, 289

• Simson Line at Interactive Geometry
• Simson Line at cut-the-knot.org
• F. M. Jackson and Weisstein, Eric W. Simson Line (англ.) на сайте Wolfram MathWorld.
• A generalization of Neuberg's theorem and the Simson-Wallace line at Dynamic Geometry Sketches, an interactive dynamic geometry sketch.