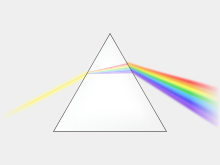
Разложение света в спектр вследствие дисперсии при прохождении через призму (опыт Ньютона) У этого термина существуют и другие значения, см.
Дисперсия .
Диспе́рсия све́та (разложение света ; светорассеяние [ 1] явлений , обусловленных зависимостью абсолютного показателя преломления вещества от частоты (или длины волны ) света (частотная дисперсия), или, что то же самое, зависимостью фазовой скорости света в веществе от частоты (или длины волны). Экспериментально открыта Исааком Ньютоном около 1672 года , хотя теоретически достаточно хорошо объяснена значительно позднее[ 2]
Пространственной дисперсией называется зависимость тензора диэлектрической проницаемости среды от волнового вектора . Такая зависимость вызывает ряд явлений, называемых эффектами пространственной поляризации.
Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является различие фазовых скоростей распространения лучей света c различной длиной волны в прозрачном веществе — оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и, следовательно, цвета). Обычно, чем меньше длина световой волны, тем больше показатель преломления среды для неё и тем меньше фазовая скорость волны в среде:
у света красного цвета фазовая скорость распространения в среде максимальна, а степень преломления — минимальна, у света фиолетового цвета фазовая скорость распространения в среде минимальна, а степень преломления — максимальна. Однако в некоторых веществах (например, в парах иода ) наблюдается эффект аномальной дисперсии , при котором синие лучи преломляются меньше, чем красные, а другие лучи поглощаются веществом и от наблюдения ускользают. Говоря строже, аномальная дисперсия широко распространена, например, она наблюдается практически у всех газов на частотах вблизи линий поглощения, однако у паров иода она достаточно удобна для наблюдения в оптическом диапазоне, где они очень сильно поглощают свет.
Дисперсия света позволила впервые вполне убедительно показать составную природу белого света.
Белый свет разлагается в спектр в результате прохождения через дифракционную решётку или отражения от неё (это не связано с явлением дисперсии, а объясняется природой дифракции). Дифракционный и призматический спектры несколько отличаются: призматический спектр сжат в красной части и растянут в фиолетовой и располагается в порядке убывания длины волны: от красного к фиолетовому; нормальный (дифракционный) спектр — равномерный во всех областях и располагается в порядке возрастания длин волн: от фиолетового к красному.
По аналогии с дисперсией света, также дисперсией называются и сходные явления зависимости распространения волн любой другой природы от длины волны (или частоты). По этой причине, например, термин закон дисперсии , применяемый как название количественного соотношения, связывающего частоту и волновое число , применяется не только к электромагнитной волне , но к любому волновому процессу.
Дисперсией объясняется факт появления радуги после дождя (точнее тот факт, что радуга разноцветная, а не белая).
Дисперсия является причиной хроматических аберраций — одних из аберраций оптических систем , в том числе фотографических и видеообъективов .
Огюстен Коши предложил эмпирическую формулу для аппроксимации зависимости показателя преломления среды от длины волны:
n = a + b / λ 2 + c / λ 4 {\displaystyle n=a+b/\lambda ^{2}+c/\lambda ^{4}} где λ {\displaystyle \lambda } a , b , c — постоянные, значения которых для каждого материала должны быть определены в опыте. В большинстве случаев можно ограничиться двумя первыми членами формулы Коши. Впоследствии были предложены другие более точные, но и одновременно более сложные, формулы аппроксимации.
Благодаря дисперсии можно наблюдать разные цвета Радуга , чьи цвета обусловлены дисперсией, — один из ключевых образов культуры и искусства.Благодаря дисперсии света можно наблюдать цветную «игру света» на гранях бриллианта и других прозрачных гранёных предметах или материалах. В той или иной степени радужные эффекты обнаруживаются достаточно часто при прохождении света через почти любые прозрачные предметы. В искусстве они могут специально усиливаться и/или подчёркиваться. Разложение света в спектр (вследствие дисперсии) при преломлении в призме — довольно распространённая тема в изобразительном искусстве. Например, на обложке альбома The Dark Side of the Moon группы Pink Floyd изображено преломление света в призме с разложением в спектр.
[ править | править код ] Описание хроматической дисперсии с помощью пертурбативного подхода через коэффициенты Тейлора подходит для задач оптимизации, где необходимо сбалансировать дисперсию от нескольких различных систем. Например, в лазерных усилителях, импульсы сначала растягиваются во времени, чтобы избежать оптического повреждения кристаллов. Затем, в процессе усиления энергии, импульсы накапливают неизбежную линейную и нелинейную фазу, проходя через различные материалы. Наконец, импульсы сжимаются в различных типах компрессоров. Для того чтобы сбросить любые остаточные высшие порядки в накопленной фазе, отдельные порядки дисперсии обычно измеряются и балансируются. Для однородных систем такое пертурбативное описание часто не требуется (например, для распространения импульса в волноводах или оптических волокнах). Дисперсионные порядки сводятся к аналитическим уравнениям, которые идентичны преобразованиям типа Лаха-Лагера[ 3] [ 4]
Порядки дисперсии определяются разложением Тейлора фазы или волнового вектора.
φ ( ω ) = φ | ω 0 + ∂ φ ∂ ω | ω 0 ( ω − ω 0 ) + 1 2 ∂ 2 φ ∂ ω 2 | ω 0 ( ω − ω 0 ) 2 + … + 1 p ! ∂ p φ ∂ ω p | ω 0 ( ω − ω 0 ) p + … {\displaystyle {\begin{array}{c}\varphi \mathrm {(} \omega \mathrm {)} =\varphi \left.\ \right|_{\omega _{0}}+\left.\ {\frac {\partial \varphi }{\partial \omega }}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)+{\frac {1}{2}}\left.\ {\frac {\partial ^{2}\varphi }{\partial \omega ^{2}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{2}\ +\ldots +{\frac {1}{p!}}\left.\ {\frac {\partial ^{p}\varphi }{\partial \omega ^{p}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{p}+\ldots \end{array}}}
k ( ω ) = k | ω 0 + ∂ k ∂ ω | ω 0 ( ω − ω 0 ) + 1 2 ∂ 2 k ∂ ω 2 | ω 0 ( ω − ω 0 ) 2 + … + 1 p ! ∂ p k ∂ ω p | ω 0 ( ω − ω 0 ) p + … {\displaystyle {\begin{array}{c}k\mathrm {(} \omega \mathrm {)} =k\left.\ \right|_{\omega _{0}}+\left.\ {\frac {\partial k}{\partial \omega }}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)+{\frac {1}{2}}\left.\ {\frac {\partial ^{2}k}{\partial \omega ^{2}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{2}\ +\ldots +{\frac {1}{p!}}\left.\ {\frac {\partial ^{p}k}{\partial \omega ^{p}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{p}+\ldots \end{array}}}
Производные дисперсии для волнового вектора k ( ω ) = ω c n ( ω ) {\displaystyle k\mathrm {(} \omega \mathrm {)} ={\frac {\omega }{c}}n\mathrm {(} \omega \mathrm {)} } φ ( ω ) = ω c O P ( ω ) {\displaystyle \varphi \mathrm {(} \omega \mathrm {)} ={\frac {\omega }{c}}{\it {OP}}\mathrm {(} \omega \mathrm {)} }
∂ p ∂ ω p k ( ω ) = 1 c ( p ∂ p − 1 ∂ ω p − 1 n ( ω ) + ω ∂ p ∂ ω p n ( ω ) ) {\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}k\mathrm {(} \omega \mathrm {)} ={\frac {1}{c}}\left(p{\frac {{\partial }^{p-1}}{\partial {\omega }^{p-1}}}n\mathrm {(} \omega \mathrm {)} +\omega {\frac {{\partial }^{p}}{\partial {\omega }^{p}}}n\mathrm {(} \omega \mathrm {)} \right)\ \end{array}}} ∂ p ∂ ω p φ ( ω ) = 1 c ( p ∂ p − 1 ∂ ω p − 1 O P ( ω ) + ω ∂ p ∂ ω p O P ( ω ) ) ( 1 ) {\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}\varphi \mathrm {(} \omega \mathrm {)} ={\frac {1}{c}}\left(p{\frac {{\partial }^{p-1}}{\partial {\omega }^{p-1}}}{\it {OP}}\mathrm {(} \omega \mathrm {)} +\omega {\frac {{\partial }^{p}}{\partial {\omega }^{p}}}{\it {OP}}\mathrm {(} \omega \mathrm {)} \right)\end{array}}(1)}
Производные любой дифференцируемой функции f ( ω | λ ) {\displaystyle f\mathrm {(} \omega \mathrm {|} \lambda \mathrm {)} }
∂ p ∂ ω p f ( ω ) = ( − 1 ) p ( λ 2 π c ) p ∑ m = 0 p A ( p , m ) λ m ∂ m ∂ λ m f ( λ ) {\displaystyle {\begin{array}{l}{\frac {\partial {p}}{\partial {\omega }^{p}}}f\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}f\mathrm {(} \lambda \mathrm {)} }\end{array}}} , {\displaystyle ,} ∂ p ∂ λ p f ( λ ) = ( − 1 ) p ( ω 2 π c ) p ∑ m = 0 p A ( p , m ) ω m ∂ m ∂ ω m f ( ω ) ( 2 ) {\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\lambda }^{p}}}f\mathrm {(} \lambda \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\omega }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\omega }^{m}{\frac {{\partial }^{m}}{\partial {\omega }^{m}}}f\mathrm {(} \omega \mathrm {)} }\end{array}}(2)}
Матричные элементы преобразования являются коэффициентами Лаха: A ( p , m ) = p ! ( p − m ) ! m ! ( p − 1 ) ! ( m − 1 ) ! {\displaystyle {\mathcal {A}}\mathrm {(} p,m\mathrm {)} ={\frac {p\mathrm {!} }{\left(p\mathrm {-} m\right)\mathrm {!} m\mathrm {!} }}{\frac {\mathrm {(} p\mathrm {-} \mathrm {1)!} }{\mathrm {(} m\mathrm {-} \mathrm {1)!} }}}
Записанное для дисперсии групповой скорости GDD, приведенное выше выражение утверждает, что постоянная длины волны GGD будет иметь нулевые высшие порядки. Высшие порядки, полученные из GDD, являются:
∂ p ∂ ω p G D D ( ω ) = ( − 1 ) p ( λ 2 π c ) p ∑ m = 0 p A ( p , m ) λ m ∂ m ∂ λ m G D D ( λ ) {\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}GDD\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}GDD\mathrm {(} \lambda \mathrm {)} }\end{array}}}
Подстановка уравнения (2), выраженного для показателя преломления n {\displaystyle n} O P {\displaystyle OP} p t h {\displaystyle p^{th}}
P O D = d p φ ( ω ) d ω p = ( − 1 ) p ( λ 2 π c ) ( p − 1 ) ∑ m = 0 p B ( p , m ) ( λ ) m d m O P ( λ ) d λ m {\displaystyle POD={\frac {d^{p}\varphi (\omega )}{d\omega ^{p}}}=(-1)^{p}({\frac {\lambda }{2\pi c}})^{(p-1)}\sum _{m=0}^{p}{\mathcal {B(p,m)}}(\lambda )^{m}{\frac {d^{m}OP(\lambda )}{d\lambda ^{m}}}} , {\displaystyle ,} P O D = d p k ( ω ) d ω p = ( − 1 ) p ( λ 2 π c ) ( p − 1 ) ∑ m = 0 p B ( p , m ) ( λ ) m d m n ( λ ) d λ m {\displaystyle POD={\frac {d^{p}k(\omega )}{d\omega ^{p}}}=(-1)^{p}({\frac {\lambda }{2\pi c}})^{(p-1)}\sum _{m=0}^{p}{\mathcal {B(p,m)}}(\lambda )^{m}{\frac {d^{m}n(\lambda )}{d\lambda ^{m}}}}
Матричные элементы преобразований представляют собой беззнаковые коэффициенты Лагерра порядка минус 2 и имеют вид: B ( p , m ) = p ! ( p − m ) ! m ! ( p − 2 ) ! ( m − 2 ) ! {\displaystyle {\mathcal {B}}\mathrm {(} p,m\mathrm {)} ={\frac {p\mathrm {!} }{\left(p\mathrm {-} m\right)\mathrm {!} m\mathrm {!} }}{\frac {\mathrm {(} p\mathrm {-} \mathrm {2)!} }{\mathrm {(} m\mathrm {-} \mathrm {2)!} }}}
Первые десять порядков дисперсии, записанные в явном виде для волнового вектора:
G D = ∂ ∂ ω k ( ω ) = 1 c ( n ( ω ) + ω ∂ n ( ω ) ∂ ω ) = 1 c ( n ( λ ) − λ ∂ n ( λ ) ∂ λ ) = v g r − 1 {\displaystyle {\begin{array}{l}{\boldsymbol {\it {GD}}}={\frac {\partial }{\partial \omega }}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(n\mathrm {(} \omega \mathrm {)} +\omega {\frac {\partial n\mathrm {(} \omega \mathrm {)} }{\partial \omega }}\right)={\frac {\mathrm {1} }{c}}\left(n\mathrm {(} \lambda \mathrm {)} -\lambda {\frac {\partial n\mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}\right)=v_{gr}^{\mathrm {-} \mathrm {1} }\end{array}}}
Групповой показатель преломления n g {\displaystyle n_{g}} n g = c v g r − 1 {\displaystyle n_{g}=cv_{gr}^{\mathrm {-} \mathrm {1} }}
G D D = ∂ 2 ∂ ω 2 k ( ω ) = 1 c ( 2 ∂ n ( ω ) ∂ ω + ω ∂ 2 n ( ω ) ∂ ω 2 ) = 1 c ( λ 2 π c ) ( λ 2 ∂ 2 n ( λ ) ∂ λ 2 ) {\displaystyle {\begin{array}{l}{\boldsymbol {\it {GDD}}}={\frac {{\partial }^{2}}{\partial {\omega }^{\mathrm {2} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {2} {\frac {\partial n\mathrm {(} \omega \mathrm {)} }{\partial \omega }}+\omega {\frac {{\partial }^{2}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}\right)={\frac {\mathrm {1} }{c}}\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)\left({\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}\right)\end{array}}}
T O D = ∂ 3 ∂ ω 3 k ( ω ) = 1 c ( 3 ∂ 2 n ( ω ) ∂ ω 2 + ω ∂ 3 n ( ω ) ∂ ω 3 ) = − 1 c ( λ 2 π c ) 2 ( 3 λ 2 ∂ 2 n ( λ ) ∂ λ 2 + λ 3 ∂ 3 n ( λ ) ∂ λ 3 ) {\displaystyle {\begin{array}{l}{\boldsymbol {\it {TOD}}}={\frac {{\partial }^{3}}{\partial {\omega }^{\mathrm {3} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {3} {\frac {{\partial }^{2}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}+\omega {\frac {{\partial }^{3}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {2} }{\Bigl (}\mathrm {3} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+{\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}{\Bigr )}\end{array}}}
F O D = ∂ 4 ∂ ω 4 k ( ω ) = 1 c ( 4 ∂ 3 n ( ω ) ∂ ω 3 + ω ∂ 4 n ( ω ) ∂ ω 4 ) = 1 c ( λ 2 π c ) 3 ( 12 λ 2 ∂ 2 n ( λ ) ∂ λ 2 + 8 λ 3 ∂ 3 n ( λ ) ∂ λ 3 + λ 4 ∂ 4 n ( λ ) ∂ λ 4 ) {\displaystyle {\begin{array}{l}{\boldsymbol {\it {FOD}}}={\frac {{\partial }^{4}}{\partial {\omega }^{\mathrm {4} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {4} {\frac {{\partial }^{3}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}+\omega {\frac {{\partial }^{4}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {3} }{\Bigl (}\mathrm {12} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {8} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+{\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}{\Bigr )}\end{array}}}
F i O D = ∂ 5 ∂ ω 5 k ( ω ) = 1 c ( 5 ∂ 4 n ( ω ) ∂ ω 4 + ω ∂ 5 n ( ω ) ∂ ω 5 ) = − 1 c ( λ 2 π c ) 4 ( 60 λ 2 ∂ 2 n ( λ ) ∂ λ 2 + 60 λ 3 ∂ 3 n ( λ ) ∂ λ 3 + 15 λ 4 ∂ 4 n ( λ ) ∂ λ 4 + λ 5 ∂ 5 n ( λ ) ∂ λ 5 ) {\displaystyle {\begin{array}{l}{\boldsymbol {\it {FiOD}}}={\frac {{\partial }^{5}}{\partial {\omega }^{\mathrm {5} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {5} {\frac {{\partial }^{4}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}+\omega {\frac {{\partial }^{5}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {4} }{\Bigl (}\mathrm {60} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {60} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {15} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}{\Bigr )}\end{array}}}
S i O D = ∂ 6 ∂ ω 6 k ( ω ) = 1 c ( 6 ∂ 5 n ( ω ) ∂ ω 5 + ω ∂ 6 n ( ω ) ∂ ω 6 ) = 1 c ( λ 2 π c ) 5 ( 360 λ 2 ∂ 2 n ( λ ) ∂ λ 2 + 480 λ 3 ∂ 3 n ( λ ) ∂ λ 3 + 180 λ 4 ∂ 4 n ( λ ) ∂ λ 4 + 24 λ 5 ∂ 5 n ( λ ) ∂ λ 5 + λ 6 ∂ 6 n ( λ ) ∂ λ 6 ) {\displaystyle {\begin{array}{l}{\boldsymbol {\it {SiOD}}}={\frac {{\partial }^{6}}{\partial {\omega }^{\mathrm {6} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {6} {\frac {{\partial }^{5}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}+\omega {\frac {{\partial }^{6}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {6} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {5} }{\Bigl (}\mathrm {360} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {480} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {180} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {24} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+{\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}{\Bigr )}\end{array}}}
S e O D = ∂ 7 ∂ ω 7 k ( ω ) = 1 c ( 7 ∂ 6 n ( ω ) ∂ ω 6 + ω ∂ 7 n ( ω ) ∂ ω 7 ) = − 1 c ( λ 2 π c ) 6 ( 2520 λ 2 ∂ 2 n ( λ ) ∂ λ 2 + 4200 λ 3 ∂ 3 n ( λ ) ∂ λ 3 + 2100 λ 4 ∂ 4 n ( λ ) ∂ λ 4 + 420 λ 5 ∂ 5 n ( λ ) ∂ λ 5 + 35 λ 6 ∂ 6 n ( λ ) ∂ λ 6 + λ 7 ∂ 7 n ( λ ) ∂ λ 7 ) {\displaystyle {\begin{array}{l}{\boldsymbol {\it {SeOD}}}={\frac {{\partial }^{7}}{\partial {\omega }^{\mathrm {7} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {7} {\frac {{\partial }^{6}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {6} }}}+\omega {\frac {{\partial }^{7}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {7} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {6} }{\Bigl (}\mathrm {2520} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {4200} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {2100} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {420} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {35} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+{\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}{\Bigr )}\end{array}}}
E O D = ∂ 8 ∂ ω 8 k ( ω ) = 1 c ( 8 ∂ 7 n ( ω ) ∂ ω 7 + ω ∂ 8 n ( ω ) ∂ ω 8 ) = 1 c ( λ 2 π c ) 7 ( 20160 λ 2 ∂ 2 n ( λ ) ∂ λ 2 + 40320 λ 3 ∂ 3 n ( λ ) ∂ λ 3 + 25200 λ 4 ∂ 4 n ( λ ) ∂ λ 4 + 6720 λ 5 ∂ 5 n ( λ ) ∂ λ 5 + 840 λ 6 ∂ 6 n ( λ ) ∂ λ 6 + + 48 λ 7 ∂ 7 n ( λ ) ∂ λ 7 + λ 8 ∂ 8 n ( λ ) ∂ λ 8 ) {\displaystyle {\begin{array}{l}{\boldsymbol {\it {EOD}}}={\frac {{\partial }^{8}}{\partial {\omega }^{\mathrm {8} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {8} {\frac {{\partial }^{7}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {7} }}}+\omega {\frac {{\partial }^{8}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {7} }{\Bigl (}\mathrm {20160} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {40320} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {25200} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {6720} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {840} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {48} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+{\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}{\Bigr )}\end{array}}}
N O D = ∂ 9 ∂ ω 9 k ( ω ) = 1 c ( 9 ∂ 8 n ( ω ) ∂ ω 8 + ω ∂ 9 n ( ω ) ∂ ω 9 ) = − 1 c ( λ 2 π c ) 8 ( 181440 λ 2 ∂ 2 n ( λ ) ∂ λ 2 + 423360 λ 3 ∂ 3 n ( λ ) ∂ λ 3 + 317520 λ 4 ∂ 4 n ( λ ) ∂ λ 4 + 105840 λ 5 ∂ 5 n ( λ ) ∂ λ 5 + 17640 λ 6 ∂ 6 n ( λ ) ∂ λ 6 + + 1512 λ 7 ∂ 7 n ( λ ) ∂ λ 7 + 63 λ 8 ∂ 8 n ( λ ) ∂ λ 8 + λ 9 ∂ 9 n ( λ ) ∂ λ 9 ) {\displaystyle {\begin{array}{l}{\boldsymbol {\it {NOD}}}={\frac {{\partial }^{9}}{\partial {\omega }^{\mathrm {9} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {9} {\frac {{\partial }^{8}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}+\omega {\frac {{\partial }^{9}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {8} }{\Bigl (}\mathrm {181440} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {423360} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {317520} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {105840} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {17640} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {1512} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {63} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+{\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}{\Bigr )}\end{array}}}
T e O D = ∂ 10 ∂ ω 10 k ( ω ) = 1 c ( 10 ∂ 9 n ( ω ) ∂ ω 9 + ω ∂ 10 n ( ω ) ∂ ω 10 ) = 1 c ( λ 2 π c ) 9 ( 1814400 λ 2 ∂ 2 n ( λ ) ∂ λ 2 + 4838400 λ 3 ∂ 3 n ( λ ) ∂ λ 3 + 4233600 λ 4 ∂ 4 n ( λ ) ∂ λ 4 + 1693440 λ 5 ∂ 5 n ( λ ) ∂ λ 5 + + 352800 λ 6 ∂ 6 n ( λ ) ∂ λ 6 + 40320 λ 7 ∂ 7 n ( λ ) ∂ λ 7 + 2520 λ 8 ∂ 8 n ( λ ) ∂ λ 8 + 80 λ 9 ∂ 9 n ( λ ) ∂ λ 9 + λ 10 ∂ 10 n ( λ ) ∂ λ 10 ) {\displaystyle {\begin{array}{l}{\boldsymbol {\it {TeOD}}}={\frac {{\partial }^{10}}{\partial {\omega }^{\mathrm {10} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {10} {\frac {{\partial }^{9}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}+\omega {\frac {{\partial }^{10}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {10} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {9} }{\Bigl (}\mathrm {1814400} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {4838400} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {4233600} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{1693440}{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\\+\mathrm {352800} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\mathrm {40320} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {2520} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+\mathrm {80} {\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}+{\lambda }^{\mathrm {10} }{\frac {{\partial }^{10}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {10} }}}{\Bigr )}\end{array}}}
В явном виде, записанные для фазы φ {\displaystyle \varphi }
∂ p ∂ ω p f ( ω ) = ( − 1 ) p ( λ 2 π c ) p ∑ m = 0 p A ( p , m ) λ m ∂ m ∂ λ m f ( λ ) {\displaystyle {\begin{array}{l}{\frac {\partial {p}}{\partial {\omega }^{p}}}f\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}f\mathrm {(} \lambda \mathrm {)} }\end{array}}} , {\displaystyle ,} ∂ p ∂ λ p f ( λ ) = ( − 1 ) p ( ω 2 π c ) p ∑ m = 0 p A ( p , m ) ω m ∂ m ∂ ω m f ( ω ) {\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\lambda }^{p}}}f\mathrm {(} \lambda \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\omega }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\omega }^{m}{\frac {{\partial }^{m}}{\partial {\omega }^{m}}}f\mathrm {(} \omega \mathrm {)} }\end{array}}}
∂ φ ( ω ) ∂ ω = − ( 2 π c ω 2 ) ∂ φ ( ω ) ∂ λ = − ( λ 2 2 π c ) ∂ φ ( λ ) ∂ λ {\displaystyle {\begin{array}{l}{\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \omega }}={-}\left({\frac {\mathrm {2} \pi c}{{\omega }^{\mathrm {2} }}}\right){\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \lambda }}={-}\left({\frac {{\lambda }^{\mathrm {2} }}{\mathrm {2} \pi c}}\right){\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}\end{array}}}
∂ 2 φ ( ω ) ∂ ω 2 = ∂ ∂ ω ( ∂ φ ( ω ) ∂ ω ) = ( λ 2 π c ) 2 ( 2 λ ∂ φ ( λ ) ∂ λ + λ 2 ∂ 2 φ ( λ ) ∂ λ 2 ) {\displaystyle {\begin{array}{l}{\frac {{\partial }^{2}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}={\frac {\partial }{\partial \omega }}\left({\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \omega }}\right)={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {2} }\left(\mathrm {2} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+{\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}\right)\end{array}}}
∂ 3 φ ( ω ) ∂ ω 3 = − ( λ 2 π c ) 3 ( 6 λ ∂ φ ( λ ) ∂ λ + 6 λ 2 ∂ 2 φ ( λ ) ∂ λ 2 + λ 3 ∂ 3 φ ( λ ) ∂ λ 3 ) {\displaystyle {\begin{array}{l}{\frac {{\partial }^{3}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {3} }\left(\mathrm {6} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {6} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+{\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}\right)\end{array}}}
∂ 4 φ ( ω ) ∂ ω 4 = ( λ 2 π c ) 4 ( 24 λ ∂ φ ( λ ) ∂ λ + 36 λ 2 ∂ 2 φ ( λ ) ∂ λ 2 + 12 λ 3 ∂ 3 φ ( λ ) ∂ λ 3 + λ 4 ∂ 4 φ ( λ ) ∂ λ 4 ) {\displaystyle {\begin{array}{l}{\frac {{\partial }^{4}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {4} }{\Bigl (}\mathrm {24} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {36} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {12} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+{\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}{\Bigr )}\end{array}}}
∂ 5 φ ( ω ) ∂ ω 5 = − ( λ 2 π c ) 5 ( 120 λ ∂ φ ( λ ) ∂ λ + 240 λ 2 ∂ 2 φ ( λ ) ∂ λ 2 + 120 λ 3 ∂ 3 φ ( λ ) ∂ λ 3 + 20 λ 4 ∂ 4 φ ( λ ) ∂ λ 4 + λ 5 ∂ 5 φ ( λ ) ∂ λ 5 ) {\displaystyle {\begin{array}{l}{\frac {{\partial }^{\mathrm {5} }\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {5} }{\Bigl (}\mathrm {120} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {240} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {120} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {20} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}{\Bigr )}\end{array}}}
∂ 6 φ ( ω ) ∂ ω 6 = ( λ 2 π c ) 6 ( 720 λ ∂ φ ( λ ) ∂ λ + 1800 λ 2 ∂ 2 φ ( λ ) ∂ λ 2 + 1200 λ 3 ∂ 3 φ ( λ ) ∂ λ 3 + 300 λ 4 ∂ 4 φ ( λ ) ∂ λ 4 + 30 λ 5 ∂ 5 φ ( λ ) ∂ λ 5 + λ 6 ∂ 6 φ ( λ ) ∂ λ 6 ) {\displaystyle {\begin{array}{l}{\frac {{\partial }^{6}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {6} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {6} }{\Bigl (}\mathrm {720} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {1800} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {1200} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {300} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {30} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}\mathrm {\ +} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}{\Bigr )}\end{array}}}
∂ 7 φ ( ω ) ∂ ω 7 = − ( λ 2 π c ) 7 ( 5040 λ ∂ φ ( λ ) ∂ λ + 15120 λ 2 ∂ 2 φ ( λ ) ∂ λ 2 + 12600 λ 3 ∂ 3 φ ( λ ) ∂ λ 3 + 4200 λ 4 ∂ 4 φ ( λ ) ∂ λ 4 + 630 λ 5 ∂ 5 φ ( λ ) ∂ λ 5 + 42 λ 6 ∂ 6 φ ( λ ) ∂ λ 6 + λ 7 ∂ 7 φ ( λ ) ∂ λ 7 ) {\displaystyle {\begin{array}{l}{\frac {{\partial }^{7}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {7} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {7} }{\Bigl (}\mathrm {5040} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {15120} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {12600} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {4200} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {630} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {42} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+{\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}{\Bigr )}\end{array}}}
∂ 8 φ ( ω ) ∂ ω 8 = ( λ 2 π c ) 8 ( 40320 λ ∂ φ ( λ ) ∂ λ + 141120 λ 2 ∂ 2 φ ( λ ) ∂ λ 2 + 141120 λ 3 ∂ 3 φ ( λ ) ∂ λ 3 + 58800 λ 4 ∂ 4 φ ( λ ) ∂ λ 4 + 11760 λ 5 ∂ 5 φ ( λ ) ∂ λ 5 + 1176 λ 6 ∂ 6 φ ( λ ) ∂ λ 6 + 56 λ 7 ∂ 7 φ ( λ ) ∂ λ 7 + + λ 8 ∂ 8 φ ( λ ) ∂ λ 8 ) {\displaystyle {\begin{array}{l}{\frac {{\partial }^{8}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {8} }{\Bigl (}\mathrm {40320} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {141120} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {141120} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {58800} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {11760} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {1176} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\mathrm {56} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\\+{\lambda }^{\mathrm {8} }{\frac {\partial ^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}{\Bigr )}\end{array}}} ∂ 9 φ ( ω ) ∂ ω 9 = − ( λ 2 π c ) 9 ( 362880 λ ∂ φ ( λ ) ∂ λ + 1451520 λ 2 ∂ 2 φ ( λ ) ∂ λ 2 + 1693440 λ 3 ∂ 3 φ ( λ ) ∂ λ 3 + 846720 λ 4 ∂ 4 φ ( λ ) ∂ λ 4 + 211680 λ 5 ∂ 5 φ ( λ ) ∂ λ 5 + 28224 λ 6 ∂ 6 φ ( λ ) ∂ λ 6 + + 2016 λ 7 ∂ 7 φ ( λ ) ∂ λ 7 + 72 λ 8 ∂ 8 φ ( λ ) ∂ λ 8 + λ 9 ∂ 9 φ ( λ ) ∂ λ 9 ) {\displaystyle {\begin{array}{l}{\frac {{\partial }^{9}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {9} }{\Bigl (}\mathrm {362880} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {1451520} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {1693440} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {846720} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {211680} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {28224} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {2016} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {72} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+{\lambda }^{\mathrm {9} }{\frac {\partial ^{\mathrm {9} }\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}{\Bigr )}\end{array}}}
∂ 10 φ ( ω ) ∂ ω 10 = ( λ 2 π c ) 10 ( 3628800 λ ∂ φ ( λ ) ∂ λ + 16329600 λ 2 ∂ 2 φ ( λ ) ∂ λ 2 + 21772800 λ 3 ∂ 3 φ ( λ ) ∂ λ 3 + 12700800 λ 4 ∂ 4 φ ( λ ) ∂ λ 4 + 3810240 λ 5 ∂ 5 φ ( λ ) ∂ λ 5 + 635040 λ 6 ∂ 6 φ ( λ ) ∂ λ 6 + + 60480 λ 7 ∂ 7 φ ( λ ) ∂ λ 7 + 3240 λ 8 ∂ 8 φ ( λ ) ∂ λ 8 + 90 λ 9 ∂ 9 φ ( λ ) ∂ λ 9 + λ 10 ∂ 10 φ ( λ ) ∂ λ 10 ) {\displaystyle {\begin{array}{l}{\frac {{\partial }^{10}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {10} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {10} }{\Bigl (}\mathrm {3628800} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {16329600} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {21772800} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {12700800} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {3810240} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {635040} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {60480} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {3240} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+\mathrm {90} {\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}+{\lambda }^{\mathrm {10} }{\frac {{\partial }^{10}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {10} }}}{\Bigr )}\end{array}}}
↑ Егоров Н. Г. Светорассеяние Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб. , 1890—1907.↑ Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов М. : Большая российская энциклопедия, 2004—2017.↑ Popmintchev, Dimitar; Wang, Siyang; Xiaoshi, Zhang; Stoev, Ventzislav; Popmintchev, Tenio (2022-10-24). "Analytical Lah-Laguerre optical formalism for perturbative chromatic dispersion" . Optics Express (англ.) . 30 (22): 40779–40808. Bibcode :2022OExpr..3040779P . doi :10.1364/OE.457139 {{cite journal }}: Википедия:Обслуживание CS1 (дата и год) (ссылка )↑ Popmintchev, Dimitar; Wang, Siyang; Xiaoshi, Zhang; Stoev, Ventzislav; Popmintchev, Tenio (2020-08-30). "Theory of the Chromatic Dispersion, Revisited" . arXiv (англ.) . Bibcode :2020arXiv201100066P . doi :10.48550/ARXIV.2011.00066 Яштолд-Говорко В. А. Фотосъёмка и обработка. Съёмка, формулы, термины, рецепты. — Изд. 4-е, сокр. — М. : Искусство, 1977.Ссылки на внешние ресурсы
В библиографических каталогах