Теорема Дезарга

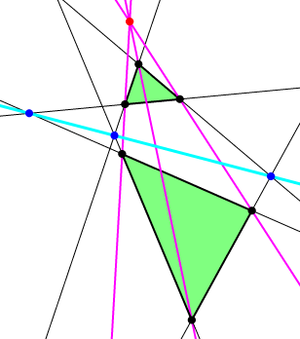
Теорема Дезарга является одной из основных теорем проективной геометрии.

Если два треугольника расположены на плоскости таким образом, что прямые, соединяющие соответственные вершины треугольников, проходят через одну точку, то три точки, в которых пересекаются продолжения трёх пар соответственных сторон треугольников, лежат на одной прямой.

Обратное тоже верно:

Если два треугольника расположены на плоскости таким образом, что три точки, в которых пересекаются продолжения трёх пар соответственных сторон треугольников, лежат на одной прямой, то прямые, соединяющие соответственные вершины треугольников, проходят через одну точку.

• Эти две теоремы являются двойственными по отношению друг к другу, и иногда объединяются в единую теорему, которая формулируется так: «Два треугольника имеют центр перспективы^[1] тогда и только тогда, когда они имеют ось перспективы^[2]».
• Теорема Дезарга выполняется не во всех проективных плоскостях. Плоскости, в которых теорема выполняется, называются дезарговыми. Например, вещественная проективная плоскость дезаргова, а плоскость Молтона — недезаргова.

• Одно из самых распространённых доказательств основывается на переходе в трёхмерное пространство — достаточно представить оба треугольника двумя сечениями трёхгранной пирамиды. Вся картина при этом рассматривается как проекция на плоскость пространственной структуры.
• Другое доказательство состоит в применении проективного преобразования, которое переводит две из пересечений продолжений сторон на идеальную прямую. После этого остаётся доказать параллельность третьей пары сторон. Последнее легко видеть из подобия треугольников.
• Ещё одно доказательство состоит в трёхкратном использовании теоремы Менелая.

Понселе основал на теореме Дезарга свою изящную теорию гомологических фигур. Он называл два треугольника, о которых идет речь в теореме Дезарга, гомологическими, точку пересечения прямых, соединяющих попарно их вершины — центром гомологии, а прямую, на которой попарно пересекаются их стороны, — осью гомологии.

Понселе дал следующую теорему для геометрии в пространстве, как соответствующую теореме Дезарга на плоскости:

Эта теорема может быть обобщена ещё далее следующим образом:

Точки и прямые в теореме Дезарга образуют так называемую конфигурацию Дезарга. Здесь через каждую из 10 точек проходят 3 прямые и на каждой из 10 прямых лежат 3 точки. При этом любая из 10 точек может быть принята за «вершину трёхгранной пирамиды» («дезаргову точку») в приведённом выше доказательстве. Любая прямая может быть взята как «дезаргова прямая». Фиксирование дезарговой точки или дезарговой прямой полностью определяет всю конфигурацию.

При построении проективной геометрии плоскости без выхода в трёхмерное пространство, теорема Дезарга не выводится из основных аксиом проективной плоскости. Это означает, что возможно построить проективную плоскость, где теорема Дезарга неверна. Например, плоскость Кэли — проективная плоскость над алгеброй Кэли ${\displaystyle \mathbb {O} }$ не является дезарговой (см. также недезаргова геометрия).

При построении дезарговой проективной плоскости утверждение теоремы Дезарга добавляют к системе аксиом проективной плоскости в качестве ещё одной аксиомы.

Теорема Дезарга была открыта французским геометром Дезаргом: она, вместе с двумя другими, из которых одна есть её обратная, была помещена в конце сочинения Traité de perspective, составленного Боссом согласно началам и методу Дезарга и появившегося в 1636 году. В этом сочинении было отмечено, что это утверждение очевидно, когда треугольники находятся в двух разных плоскостях; рассмотрение же случая, когда они лежат в одной плоскости, доставляет один из первых примеров употребления теоремы Менелая у новых геометров. Известность теорема Дезарга получила в начале XIX века благодаря её употреблению в работах Брианшона и Понселе.

• Теорема Паппа

• Шаль, Мишель. Исторический обзор происхождения и развития геометрических методов. Т. 1, § 28. М., 1883.
• Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
• Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 74-76. — ISBN 5-94057-170-0.