Abgeschlossene Menge

In dem Teilgebiet Topologie der Mathematik ist eine abgeschlossene Menge eine Teilmenge eines topologischen Raums, deren Komplement eine offene Menge ist.

Ein einfaches Beispiel ist das Intervall ${\displaystyle [0,1]}$ in den reellen Zahlen (mit der Standardtopologie, erzeugt durch die Metrik ${\displaystyle d_{xy}=\left|x-y\right|}$). Das Komplement von ${\displaystyle [0,1]}$ ist die Vereinigung ${\displaystyle \textstyle (-\infty ,0)\cup (1,\infty )}$ zweier offener Intervalle, also eine offene Menge, also ist ${\displaystyle [0,1]}$ eine abgeschlossene Menge. Deshalb nennt man das Intervall ${\displaystyle [0,1]}$ ein abgeschlossenes Intervall. Dagegen ist das Intervall ${\displaystyle (0,1]}$ nicht abgeschlossen, denn das Komplement ${\displaystyle (-\infty ,0]\cup (1,\infty )}$ ist nicht offen.

Ob eine Menge abgeschlossen ist oder nicht, hängt von dem Raum ab, in dem sie liegt. Die Menge der Zahlen ${\displaystyle x}$ mit ${\displaystyle 0\leq x\leq 1}$ bildet eine abgeschlossene Menge in den reellen Zahlen, aber nicht in den rationalen Zahlen mit der Standardtopologie. Dies folgt daraus, dass es Folgen mit rationalen Folgengliedern gibt, die zu einer Zahl außerhalb der rationalen Zahlen konvergieren.

Es ist zu beachten, dass der Begriff „offene Menge“ nicht das Gegenteil von „abgeschlossene Menge“ ist: Es gibt Mengen, die weder abgeschlossen noch offen sind, wie das Intervall ${\displaystyle (0,1]}$, und Mengen, die beides sind, wie die leere Menge. Solche Mengen, die gleichzeitig offen und abgeschlossen sind, werden als abgeschlossene offene Mengen bezeichnet.

Der Begriff der abgeschlossenen Menge lässt sich auf verschiedenen Abstraktionsstufen definieren. Im Folgenden werden hier der anschauliche euklidische Raum, dann metrische Räume und schließlich topologische Räume betrachtet.

Ist U eine Teilmenge des n-dimensionalen euklidischen Raums ${\displaystyle \mathbb {R} ^{n}}$, dann nennt man U abgeschlossen, falls gilt:

Für jedes ${\displaystyle x\in \mathbb {R} ^{n}}$ außerhalb von U gibt es ein ${\displaystyle \varepsilon >0}$, so dass jeder Punkt ${\displaystyle y\in \mathbb {R} ^{n}}$ mit ${\displaystyle \|x-y\|<\varepsilon }$, ebenfalls außerhalb U liegt.

Beachte, dass das ε vom Punkt x abhängt, d. h. für verschiedene Punkte gibt es verschiedene ε. Anschaulich ist die Menge der Punkte, deren Abstand von x kleiner ist als ε, eine Kugel, und zwar nur das Innere ohne die Oberfläche. Man nennt sie deshalb auch eine offene Kugel. (Im ${\displaystyle \mathbb {R} ^{2}}$ ist diese Kugel das Innere eines Kreises.)

Die Menge aller Punkte, deren Abstand von einem Punkt x kleiner oder gleich einer positiven Zahl r ist, ist auch eine Kugel, man nennt sie abgeschlossene Kugel, da sie die Definition einer abgeschlossenen Menge erfüllt.

Ist M eine abgeschlossene Teilmenge des ${\displaystyle \mathbb {R} ^{n}}$ und ${\displaystyle (x_{n})}$ eine Folge von Elementen von M, die im ${\displaystyle \mathbb {R} ^{n}}$ konvergiert, dann liegt der Grenzwert von ${\displaystyle (x_{n})}$ ebenfalls in M. Diese Eigenschaft kann alternativ benutzt werden, um abgeschlossene Teilmengen des ${\displaystyle \mathbb {R} ^{n}}$ zu definieren.

Jede abgeschlossene Menge U vom ${\displaystyle \mathbb {R} ^{n}}$ lässt sich als Durchschnitt von abzählbar vielen offenen Mengen darstellen. Zum Beispiel ist das abgeschlossene Intervall [0,1] der Durchschnitt der offenen Intervalle  ${\displaystyle \textstyle \left(-{\frac {1}{n}},1+{\frac {1}{n}}\right)}$   für alle natürlichen Zahlen n.

Sei ${\displaystyle (X,d)}$ ein metrischer Raum und ${\displaystyle U}$ eine Teilmenge von ${\displaystyle X}$. Dann nennt man ${\displaystyle U}$ abgeschlossen, wenn gilt:

Für jedes ${\displaystyle x}$ aus ${\displaystyle X\setminus U}$ gibt es eine reelle Zahl ${\displaystyle \varepsilon >0}$, so dass für jeden Punkt ${\displaystyle y}$ aus ${\displaystyle X}$ gilt: Aus ${\displaystyle d(x,y)<\varepsilon }$ folgt, dass ${\displaystyle y}$ in ${\displaystyle X\setminus U}$ liegt.

Auch hier hängt die Wahl von ${\displaystyle \varepsilon }$ von ${\displaystyle x}$ ab.

Das ist gleichbedeutend mit folgender Eigenschaft: Ist ${\displaystyle (a_{n})}$ eine Folge von Elementen aus U, die in X konvergiert, dann liegt der Grenzwert in U.

In Analogie zum euklidischen Raum nennt man die Menge der Punkte y, deren Abstand d(x,y) zu x kleiner oder gleich ε ist, eine abgeschlossene Kugel. Formal schreibt man

${\displaystyle {\overline {B}}_{r}(x):=\{\,y\in X\mid d(x,y)\leq r\,\}}$

und nennt diese Menge die abgeschlossene Kugel in X mit Mittelpunkt x und reellem Radius r > 0.

Bei der abgeschlossenen Kugel wird der Rand bzw. die Hülle der Kugel mit einbezogen: Alle y der Grundmenge X die zum Mittelpunkt x einen Abstand haben, der kleiner oder gleich r ist, gehören zur Kugel. (Beachte die im Artikel Norm (Mathematik) gegebenen Beispiele, dass eine Kugel bezüglich einer Metrik nicht immer „kugelförmig“ bzw. „kreisförmig“ ist.)

Die Definition einer abgeschlossenen Menge lässt sich nun so schreiben:

Sei (X,d) ein metrischer Raum. Dann heißt eine Teilmenge U von X abgeschlossen, falls gilt:

${\displaystyle \forall {x\in X\setminus U}:{\exists \varepsilon }>{0}:B_{\varepsilon }(x)\cap U=\emptyset }$

Diese Definition ist eine Verallgemeinerung der Definition für euklidische Räume, denn jeder euklidische Raum ist ein metrischer Raum, und für euklidische Räume stimmen die Definitionen überein.

Betrachtet man die reellen Zahlen ${\displaystyle \mathbb {R} }$ mit der üblichen euklidischen Metrik, so sind die folgenden Beispiele abgeschlossene Mengen:

• Das oben genannte abgeschlossene Intervall ${\displaystyle [0,1]}$, das sind alle Zahlen zwischen 0 und 1 einschließlich. Dieses Intervall ist auch ein Beispiel für eine abgeschlossene Kugel in ${\displaystyle \mathbb {R} }$: Der Mittelpunkt ist 1/2, der Radius ist 1/2.
• jede einelementige Menge ${\displaystyle \{a\}}$.
• ${\displaystyle \mathbb {R} }$ selbst ist abgeschlossen (und offen).
• Die leere Menge ist abgeschlossen (und offen).
• Die Menge ${\displaystyle \mathbb {Q} }$ der rationalen Zahlen ist abgeschlossen in ${\displaystyle \mathbb {Q} }$, aber nicht abgeschlossen in ${\displaystyle \mathbb {R} }$.
• Das Intervall ${\displaystyle [0,\pi )}$ ist nicht abgeschlossen in ${\displaystyle \mathbb {R} }$ (${\displaystyle \pi }$ ist die Kreiszahl Pi), die Menge aller rationalen Zahlen ${\displaystyle x}$ mit ${\displaystyle 0\leq x<\pi }$ ist dagegen abgeschlossen in ${\displaystyle \mathbb {Q} }$.
• Endliche Mengen sind stets abgeschlossen.
• Als nicht-triviales Beispiel kann man eine offene Grundmenge nehmen, z. B. ${\displaystyle (0,3)}$. Auf dieser Menge ist das Intervall ${\displaystyle (0,3)}$ selbst abgeschlossen, da jede Menge in sich abgeschlossen ist.

Im ${\displaystyle \mathbb {R} ^{2}}$ kann man sich abgeschlossene Mengen vorstellen als Mengen, die ihren Rand enthalten.

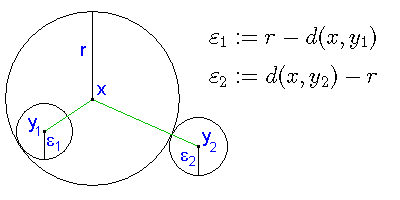
Jede abgeschlossene Kugel ist eine abgeschlossene Menge. Der Beweis dazu wird von nebenstehender Abbildung veranschaulicht: Zum Punkt ${\displaystyle y_{2}}$ außerhalb der abgeschlossenen Kugel ${\displaystyle {\overline {B}}(x,r)}$ findet man ein ${\displaystyle \epsilon _{2}}$, nämlich ${\displaystyle \epsilon _{2}=d(x,y_{2})-r}$, so dass ${\displaystyle B(y_{2},\epsilon _{2})}$ ganz außerhalb von ${\displaystyle B(x,r)}$ liegt. Analog sieht man an dieser Darstellung, dass jede offene Kugel offen ist.

Die Vereinigung von zwei abgeschlossenen Mengen ist wieder eine abgeschlossene Menge. Daraus kann man folgern, dass die Vereinigung endlich vieler abgeschlossener Mengen abgeschlossen ist. Die Vereinigung unendlich vieler abgeschlossener Mengen muss jedoch nicht abgeschlossen sein. Vereinigt man alle einelementigen Mengen ${\displaystyle \textstyle \left\{{\tfrac {1}{a}}\right\}}$ für ${\displaystyle a\in \mathbb {N} }$ ist die resultierende Menge weder offen noch abgeschlossen.

Der Durchschnitt beliebig vieler (also auch unendlich vieler) abgeschlossener Mengen ist abgeschlossen.

Um abgeschlossene Mengen in einem noch allgemeineren Kontext zu definieren, muss man das Konzept der Kugel fallen lassen. Man bezieht sich stattdessen nur auf die Offenheit des Komplements.

Ist ${\displaystyle X}$ ein topologischer Raum und ${\displaystyle U}$ eine Teilmenge von ${\displaystyle X}$, dann heißt ${\displaystyle U}$ abgeschlossen, wenn das Komplement ${\displaystyle X\setminus U}$ eine offene Menge ist.

Diese Definition ist eine Verallgemeinerung der Definition für metrische Räume.

Für jede Teilmenge ${\displaystyle U}$ eines euklidischen, metrischen oder topologischen Raumes gibt es stets eine kleinste abgeschlossene Obermenge von ${\displaystyle U}$, diese heißt abgeschlossene Hülle, auch Abschließung oder Abschluss von ${\displaystyle U}$. Man kann die abgeschlossene Hülle entweder als Durchschnitt aller abgeschlossenen Obermengen von ${\displaystyle U}$ konstruieren oder als Menge aller Grenzwerte aller konvergenten Netze, die in ${\displaystyle U}$ liegen. Auch eine analoge Charakterisierung mit Hilfe der Filterkonvergenz ist möglich. Man beachte allerdings, dass es in allgemeinen topologischen Räumen nicht mehr reicht, nur Grenzwerte von Folgen zu betrachten.

Sei ${\displaystyle U}$ eine Teilmenge eines topologischen Raumes. Dann ist es möglich, den Rand von ${\displaystyle U}$ zu definieren als den Durchschnitt der abgeschlossenen Hülle von ${\displaystyle U}$ mit der abgeschlossenen Hülle des Komplements von ${\displaystyle U}$ (oder alternativ als die abgeschlossene Hülle von ${\displaystyle U}$ ohne das Innere von ${\displaystyle U}$). Ein Punkt liegt also auf dem Rand von ${\displaystyle U}$, wenn in jeder Umgebung sowohl Punkte aus ${\displaystyle U}$ als auch Punkte aus dem Komplement von ${\displaystyle U}$ liegen. Dieser Rand-Begriff stimmt in metrischen und euklidischen Räumen mit dem intuitiven Begriff eines Randes überein. In einem topologischen Raum gilt dann allgemein:

Eine Menge ${\displaystyle U}$ ist genau dann abgeschlossen, wenn sie ihren Rand enthält.

• Boto von Querenburg: Mengentheoretische Topologie (= Springer-Lehrbuch). 3., neu bearbeitete und erweiterte Auflage. Springer, Berlin u. a. 2001, ISBN 3-540-67790-9.