ARGUS distribution
 From Wikipedia the free encyclopedia
From Wikipedia the free encyclopedia
This article relies largely or entirely on a single source. (March 2011) |
| Probability density function  c = 1. | |||
| Cumulative distribution function 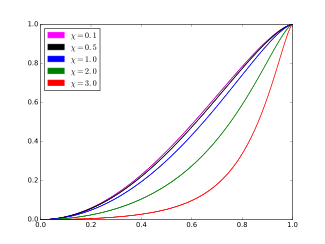 c = 1. | |||
| Parameters | cut-off (real) curvature (real) | ||
|---|---|---|---|
| Support | |||
| see text | |||
| CDF | see text | ||
| Mean | where I1 is the Modified Bessel function of the first kind of order 1, and is given in the text. | ||
| Mode | |||
| Variance | |||
In physics, the ARGUS distribution, named after the particle physics experiment ARGUS,[1] is the probability distribution of the reconstructed invariant mass of a decayed particle candidate in continuum background[clarification needed].
Definition
[edit]The probability density function (pdf) of the ARGUS distribution is:
for . Here and are parameters of the distribution and
where and are the cumulative distribution and probability density functions of the standard normal distribution, respectively.
Cumulative distribution function
[edit]The cumulative distribution function (cdf) of the ARGUS distribution is
- .
Parameter estimation
[edit]Parameter c is assumed to be known (the kinematic limit of the invariant mass distribution), whereas χ can be estimated from the sample X1, …, Xn using the maximum likelihood approach. The estimator is a function of sample second moment, and is given as a solution to the non-linear equation
- .
The solution exists and is unique, provided that the right-hand side is greater than 0.4; the resulting estimator is consistent and asymptotically normal.
Generalized ARGUS distribution
[edit]Sometimes a more general form is used to describe a more peaking-like distribution:
where Γ(·) is the gamma function, and Γ(·,·) is the upper incomplete gamma function.
Here parameters c, χ, p represent the cutoff, curvature, and power respectively.
The mode is:
The mean is:
where M(·,·,·) is the Kummer's confluent hypergeometric function.[2][circular reference]
The variance is:
p = 0.5 gives a regular ARGUS, listed above.
References
[edit]- ^ Albrecht, H. (1990). "Search for hadronic b→u decays". Physics Letters B. 241 (2): 278–282. Bibcode:1990PhLB..241..278A. doi:10.1016/0370-2693(90)91293-K. (More formally by the ARGUS Collaboration, H. Albrecht et al.) In this paper, the function has been defined with parameter c representing the beam energy and parameter p set to 0.5. The normalization and the parameter χ have been obtained from data.
- ^ Confluent hypergeometric function
Further reading
[edit]- Albrecht, H. (1994). "Measurement of the polarization in the decay B → J/ψK*". Physics Letters B. 340 (3): 217–220. Bibcode:1994PhLB..340..217A. doi:10.1016/0370-2693(94)01302-0.
- Pedlar, T.; Cronin-Hennessy, D.; Hietala, J.; Dobbs, S.; Metreveli, Z.; Seth, K.; Tomaradze, A.; Xiao, T.; Martin, L. (2011). "Observation of the hc(1P) Using e+e− Collisions above the DD Threshold". Physical Review Letters. 107 (4): 041803. arXiv:1104.2025. Bibcode:2011PhRvL.107d1803P. doi:10.1103/PhysRevLett.107.041803. PMID 21866994. S2CID 33751212.
- Lees, J. P.; Poireau, V.; Prencipe, E.; Tisserand, V.; Garra Tico, J.; Grauges, E.; Martinelli, M.; Palano, A.; Pappagallo, M.; Eigen, G.; Stugu, B.; Sun, L.; Battaglia, M.; Brown, D. N.; Hooberman, B.; Kerth, L. T.; Kolomensky, Y. G.; Lynch, G.; Osipenkov, I. L.; Tanabe, T.; Hawkes, C. M.; Soni, N.; Watson, A. T.; Koch, H.; Schroeder, T.; Asgeirsson, D. J.; Hearty, C.; Mattison, T. S.; McKenna, J. A.; et al. (2010). "Search for Charged Lepton Flavor Violation in Narrow Υ Decays". Physical Review Letters. 104 (15): 151802. arXiv:1001.1883. Bibcode:2010PhRvL.104o1802L. doi:10.1103/PhysRevLett.104.151802. PMID 20481982. S2CID 14992286.





















