Experimento de Kennedy y Thorndike

El experimento de Kennedy y Thorndike, realizado por primera vez en 1932 por Roy J. Kennedy y Edward M. Thorndike, es una forma modificada del procedimiento empleado en el experimento de Michelson y Morley, que prueba la teoría de la relatividad especial.^[1]​

La modificación consiste en hacer que un brazo del aparato clásico de Michelson y Morley sea más corto que el otro. Mientras que el mencionado experimento de Michelson-Morley demostró que la velocidad de la luz es independiente de la orientación del aparato, el experimento de Kennedy y Thorndike demostró que también es independiente de la velocidad del aparato en diferentes sistemas inerciales. También sirvió como prueba para verificar indirectamente la dilatación del tiempo: mientras que el resultado negativo del experimento de Michelson y Morley puede explicarse únicamente por la contracción de Lorentz, el resultado negativo del experimento de Kennedy y Thorndike requiere la dilatación del tiempo además de la contracción de la longitud para explicar por qué no se detecta un desfase debido al movimiento de la Tierra alrededor del Sol. La primera confirmación directa de la dilatación del tiempo la logró el experimento de Ives y Stilwell. Combinando los resultados de esos tres experimentos, se puede justificar por completo la transformación de Lorentz.^[2]​

Se han realizado variantes mejoradas del experimento de Kennedy y Thorndike utilizando cavidades ópticas o un láser de alcance lunar. Para obtener una descripción general de los ensayos sobre la invariancia de Lorentz, consúltese el artículo acerca de las pruebas de la relatividad especial.

El experimento original de Michelson y Morley permitió probar únicamente la hipótesis de la contracción de Lorentz-FitzGerald. Kennedy ya había realizado varias versiones cada vez más sofisticadas del experimento de Michelson y Morley durante la década de 1920, cuando encontró una manera de comprobar también la dilatación del tiempo. En sus propias palabras:^[1]​

El principio en el que se basa este experimento es la simple proposición de que si un haz de luz homogéneo se divide […] en dos haces que, después de recorrer recorridos de diferentes longitudes, se vuelven a juntar, entonces las fases relativas […] dependerán [… ] de la velocidad del aparato a menos que la frecuencia de la luz dependa […] de la velocidad en la forma requerida por la relatividad.

Con referencia a la Fig. 1, los componentes ópticos clave se montaron dentro de una cámara de vacío V sobre una base de cuarzo fundido de dilatación térmica extremadamente baja. Una camisa de agua W permitió mantener la temperatura dentro de un margen de 0,001 °C. Un haz de luz verde monocromática procedente de una fuente de mercurio (Hg) pasaba a través de un prisma de Nicol polarizante (N) antes de entrar en la cámara de vacío, siendo dividido por un divisor de haz (B) fijado en un ángulo de Brewster para evitar reflejos no deseados en la superficie trasera. Los dos haces se dirigieron hacia dos espejos (M₁ y M₂) que se colocaron a distancias lo más divergentes posible, dada la longitud de coherencia de la línea de mercurio de 5461 Å (≈32 cm, lo que permite una diferencia en la longitud del brazo ΔL ≈ 16 cm). Los rayos reflejados se recombinaron para formar interferencias circulares (fotografiadas en P). Una hendidura en forma de S permitió registrar múltiples exposiciones con el diámetro de los anillos en una sola placa fotográfica en diferentes momentos del día.

Al hacer un brazo del experimento mucho más corto que el otro, un cambio en la velocidad de la Tierra provocaría cambios en los tiempos de viaje de los rayos de luz, de los cuales se produciría un cambio marginal a menos que la frecuencia de la fuente de luz cambiara en el mismo grado. Para determinar si se produjo tal cambio marginal, el interferómetro se hizo extremadamente estable y se fotografiaron los patrones de interferencia para su posterior comparación. Las pruebas se realizaron durante un período de muchos meses. Como no se encontró ningún cambio marginal significativo (correspondiente a una velocidad de 10 ± 10 km/s dentro del margen de error), los experimentadores concluyeron que la dilatación del tiempo se produce según lo predicho por la relatividad especial.

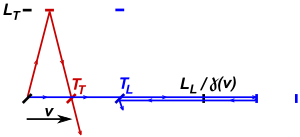
Aunque la contracción de Lorentz y FitzGerald (contracción de Lorentz) por sí sola es totalmente capaz de explicar los resultados nulos del experimento de Michelson y Morley, no puede por sí sola explicar los resultados nulos del experimento de Kennedy y Thorndike. La contracción de Lorentz y FitzGerald viene dada por la fórmula:

${\displaystyle L=L_{0}{\sqrt {1-v^{2}/c^{2}}}=L_{0}/{\gamma (v)}}$

donde

${\displaystyle L_{0}}$ es la longitud propia (la longitud del objeto en su sistema de referencia en reposo)

${\displaystyle L}$ es la longitud percibida por un observador en movimiento relativo con respecto al objeto

${\displaystyle v\,}$ es la velocidad relativa entre el observador y el objeto en movimiento, es decir entre el éter hipotético y el objeto en movimiento

${\displaystyle c\,}$ es la velocidad de la luz,

y el factor de Lorentz se define como

${\displaystyle \gamma (v)\equiv {\frac {1}{\sqrt {1-v^{2}/c^{2}}}}\ }$.

La Figura 2 ilustra un dispositivo de Kennedy y Thorndike con brazos perpendiculares y asume la validez de la contracción de Lorentz.^[3]​ Si el aparato está inmóvil con respecto al hipotético éter, la diferencia de tiempo que tarda la luz en atravesar los brazos longitudinal y transversal viene dada por:

${\displaystyle T_{L}-T_{T}={\frac {2(L_{L}-L_{T})}{c}}}$

El tiempo que tarda la luz en recorrer la longitud contraída de Lorentz del brazo longitudinal viene dado por:

${\displaystyle T_{L}=T_{1}+T_{2}={\frac {L_{L}/\gamma (v)}{c-v}}+{\frac {L_{L}/\gamma (v)}{c+v}}={\frac {2L_{L}/\gamma (v)}{c}}{\frac {1}{1-{\frac {v^{2}}{c^{2}}}}}={\frac {2L_{L}\gamma (v)}{c}}}$

donde T₁ es el tiempo de viaje en la dirección del movimiento, T₂ en la dirección opuesta, v es la componente de velocidad con respecto al éter luminífero, c es la velocidad de la luz y L_L la longitud del brazo longitudinal del interferómetro. El tiempo que tarda la luz en atravesar y retroceder el brazo transversal está dado por:

${\displaystyle T_{T}={\frac {2L_{T}}{\sqrt {c^{2}-v^{2}}}}={\frac {2L_{T}}{c}}{\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {2L_{T}\gamma (v)}{c}}}$

La diferencia de tiempo que tarda la luz en atravesar los brazos longitudinal y transversal viene dada por:

${\displaystyle T_{L}-T_{T}={\frac {2(L_{L}-L_{T})\gamma (v)}{c}}}$

Debido a que ΔL=c(T_L-T_T), se dan las siguientes diferencias de longitud de recorrido (siendo ΔL_A la diferencia de longitud de recorrido inicial y v_A la velocidad inicial del aparato, y Δ L_B y v_B después de la rotación o cambio de velocidad debido a la propia rotación de la Tierra o su rotación alrededor del Sol):^[4]​

${\displaystyle \Delta L_{A}={\frac {2\left(L_{L}-L_{T}\right)}{\sqrt {1-v_{A}^{2}/c^{2}}}},\qquad \Delta L_{B}={\frac {2\left(L_{L}-L_{T}\right)}{\sqrt {1-v_{B}^{2}/c^{2}}}}}$.

Para obtener un resultado negativo, se debería tener que ΔL_A−ΔL_B=0. Sin embargo, se puede observar que ambas fórmulas solo se anulan entre sí mientras que las velocidades sean las mismas (v_A=v_B). Pero si las velocidades son diferentes, entonces ΔL_A y ΔL_B ya no son iguales (el experimento de Michelson y Morley no se ve afectado por los cambios de velocidad, ya que la diferencia entre L_L y L_T es cero. Por lo tanto, solo prueba si la velocidad de la luz depende de la orientación del aparato). Pero en el experimento de Kennedy-Thorndike, las longitudes L_L y L_T son diferentes desde el principio, por lo que también es capaz de medir la dependencia de la velocidad de la luz sobre la velocidad del aparato.^[2]​

Según la fórmula anterior, la diferencia de longitud de recorrido ΔL_A−ΔL_B y, en consecuencia, el desplazamiento marginal esperado ΔN vienen dados por (siendo λ la longitud de onda):

${\displaystyle \Delta N={\frac {\Delta L_{A}-\Delta L_{B}}{\lambda }}={\frac {2\left(L_{L}-L_{T}\right)}{\lambda }}\left({\frac {1}{\sqrt {1-v_{A}^{2}/c^{2}}}}-{\frac {1}{\sqrt {1-v_{B}^{2}/c^{2}}}}\right)}$.

Despreciando magnitudes superiores al segundo orden en v/c:

${\displaystyle \approx {\frac {L_{L}-L_{T}}{\lambda }}\left({\frac {v_{A}^{2}-v_{B}^{2}}{c^{2}}}\right)}$

Para que ΔN sea constante, es decir, para que el desplazamiento marginal sea independiente de la velocidad o la orientación del aparato, es necesario que la frecuencia y, por tanto, la longitud de onda λ se modifiquen mediante el factor de Lorentz. En realidad, este es el caso cuando se considera el efecto de la dilatación del tiempo en la frecuencia. Por lo tanto, se requieren tanto la contracción de la longitud como la dilatación del tiempo para explicar el resultado negativo del experimento de Kennedy y Thorndike.

En 1905, Henri Poincaré y Albert Einstein demostraron que la transformación de Lorentz debe formar un grupo para satisfacer el principio de relatividad (véase historia de las transformaciones de Lorentz). Esto requiere que la contracción de la longitud y la dilatación del tiempo tengan los valores relativistas exactos. Kennedy y Thorndike argumentaron entonces que podían derivar la transformación de Lorentz completa únicamente a partir de los datos experimentales del experimento de Michelson y Morley y de su propio experimento. Pero esto no es estrictamente correcto, ya que la contracción de la longitud y la dilatación del tiempo, que tienen sus valores relativistas exactos, son suficientes pero no necesarias para la explicación de ambos experimentos. Esto se debe a que la contracción de la longitud únicamente en la dirección del movimiento es solo una posibilidad para explicar el resultado del experimento de Michelson y Morley. En general, su resultado nulo requiere que la relación entre las longitudes transversales y las longitudinales corresponda al factor de Lorentz, que incluye infinitas combinaciones de cambios de longitud en las direcciones transversal y longitudinal. Esto también afecta al papel de la dilatación del tiempo en el experimento de Kennedy y Thorndike, porque su valor depende del valor de la contracción de longitud utilizado en el análisis del experimento. Por lo tanto, es necesario considerar un tercer ensayo, el experimento de Ives y Stilwell, para justificar la transformación de Lorentz únicamente a partir de datos empíricos.^[2]​

Más precisamente: en el marco de la teoría de la prueba de Robertson-Mansouri-Sexl,^[2]​^[5]​ se puede utilizar el siguiente esquema para describir los experimentos: α representa cambios de tiempo, β cambios de longitud en la dirección del movimiento y δ cambios de longitud perpendicular a la dirección del movimiento. El experimento de Michelson y Morley prueba la relación entre β y δ, mientras que el experimento de Kennedy y Thorndike prueba la relación entre α y β. Entonces, α depende de β, que a su vez depende de δ, y en estos dos experimentos solo se pueden medir combinaciones de esas cantidades, pero no sus valores individuales. Es necesario otro experimento para medir directamente el valor de una de estas cantidades. En realidad, esto se logró con el experimento de Ives y Stilwell, que midió que α tenía el valor predicho por la dilatación del tiempo relativista. La combinación de este valor para α con el resultado nulo de Kennedy y Thorndike muestra que β necesariamente debe asumir el valor de contracción de longitud relativista. Y al combinar este valor de β con el resultado nulo de Michelson y Morley, se demuestra que δ debe ser cero. Por lo tanto, los componentes necesarios de la transformación de Lorentz, de acuerdo con los requisitos teóricos de la teoría de grupos, se obtienen mediante experimentos.

En los últimos años, los experimentos del tipo de Michelson y Morley y de Kennedy y Thorndike se han repetido con mayor precisión utilizando láser, máser y cavidades ópticas criogénicas. Se han mejorado significativamente los límites de la dependencia de la velocidad según teoría de la prueba de Robertson-Mansouri-Sexl, que indica la relación entre la dilatación del tiempo y la contracción de la longitud. Por ejemplo, el experimento original de Kennedy y Thorndike estableció límites a la dependencia de la velocidad según Robertson-Mansouri-Sexl de ~10⁻², pero los límites actuales están en el rango de ~10⁻⁸.^[5]​

La figura 3 presenta un diagrama esquemático simplificado de la repetición del experimento de Kennedy y Thorndike realizada por Braxmaier et al. en 2002.^[6]​ A la izquierda, los fotodetectores (PD) monitorean la resonancia de un resonador óptico criogénico de zafiro (CORE) de longitud estándar mantenido a temperatura de helio líquido para estabilizar la frecuencia de un láser Nd:YAG a 1064 nm. A la derecha, la línea de absorbancia de 532 nm de una referencia de yodo de baja presión se utiliza como estándar de tiempo para estabilizar la frecuencia (duplicada) de un segundo láser de Nd:YAG.

Autor	Año	Descripción	Dependencia de la velocidad máxima
Hils and Hall[7]​	1990	Comparación de la frecuencia de una cavidad óptica de Fabry–Pérot con la de un láser estabilizado en una línea de referencia I2.	${\displaystyle \lesssim 10^{-5}}$
Braxmaier et al.[6]​	2002	Comparación de la frecuencia de un resonador óptico criogénico con un estándar de frecuencia de I2, utilizando dos láseres Nd-YAG.
Wolf et al.[8]​	2003	La frecuencia de un oscilador de microondas criogénico estacionario, que consta de cristal de zafiro que funciona en modo de galería de susurros, se compara con un máser de hidrógeno cuya frecuencia se comparó con relojes de fuente atómica de cesio y rubidio. Se buscaron cambios durante la rotación de la Tierra, y se analizaron datos tomados entre 2001 y 2002.	${\displaystyle \lesssim 10^{-7}}$
Wolf et al.[9]​	2004	Véase Wolf et al. (2003). Se añadió un control activo de temperatura y se analizaron datos entre 2002 y 2003.
Tobar et al.[10]​	2009	Véase Wolf et al. (2003). Se analizaron los datos entre 2002 y 2008 para determinar las variaciones sidéreas y anuales.	${\displaystyle \lesssim 10^{-8}}$

Además de las mediciones terrestres, Müller & Soffel (1995)^[11]​ y Müller et al. llevaron a cabo experimentos del mismo tipo que el de Kennedy y Thorndike. (1999)^[12]​ Para ello, utilizaron datos de un láser de alcance lunar, en los que la distancia Tierra-Luna se evalúa con una precisión de centímetros. Si existiera un sistema de referencia preferente y la velocidad de la luz dependiera de la velocidad del observador, entonces deberían observarse oscilaciones anómalas en las mediciones de la distancia Tierra-Luna. Dado que la dilatación del tiempo ya está confirmada con alta precisión, la observación de tales oscilaciones demostraría la dependencia de la velocidad de la luz de la velocidad del observador, así como la dependencia de la dirección de la contracción de la longitud. Sin embargo, no se observaron tales oscilaciones en ninguno de los estudios, con un límite de velocidad según la teoría de Robertson-Mansouri-Sexl de ~10⁻⁵,^[12]​ comparable a los límites establecidos por Hils y Hall (1990). En consecuencia, tanto la contracción de la longitud como la dilatación del tiempo deben tener los valores predichos por la relatividad.