Augustin Fresnel

| Naissance | Broglie (France) |
|---|---|
| Décès | (à 39 ans) Ville-d'Avray (France) |
| Nationalité | |
| Résidence | France |
| Domaines | Optique |
|---|---|
| Institutions | École nationale des ponts et chaussées Académie des sciences Royal Society |
| Diplôme | École polytechnique |
| Renommé pour | Lentille de Fresnel Principe de Huygens-Fresnel Coefficients de Fresnel |
| Distinctions | Médaille Rumford |
Augustin Jean Fresnel, né le à Broglie et mort le à Ville-d'Avray, est un ingénieur et physicien français dont les recherches en optique ont conduit à l'acceptation définitive de la théorie ondulatoire de la lumière en remplacement de la théorie balistique qui s'était imposée depuis Newton. En s'appuyant sur les concepts émis par Christian Huygens à la fin du XVIIe siècle, et en procédant à ses propres expériences, il retrouva indépendamment les observations faites quelques années plus tôt par Thomas Young sur les interférences et leur donna les fondements physiques et mathématiques qui emportèrent l'adhésion des physiciens de son époque.
Dans son Mémoire sur la diffraction de la lumière, Fresnel donna la première explication rationnelle du phénomène de la diffraction. Pour sa démonstration, il montra que l'addition de deux vibrations lumineuses de même fréquence pouvait être modélisée comme la composition de deux forces, c'est-à-dire de deux vecteurs, de grandeurs et directions différentes : les vecteurs de Fresnel. En reconnaissant que la lumière est composée de vibrations transversales, Fresnel a expliqué la nature de la polarisation de la lumière, la biréfringence et la polarisation circulaire.
Bien que Fresnel puisse être considéré comme un physicien théoricien ou physicien mathématicien, il n’a eu que peu de temps pour se consacrer à ses recherches fondamentales. Son métier était ingénieur des Ponts et Chaussées. À ce titre, il a apporté des améliorations considérables à la luminosité des phares en inventant les lentilles à échelons, ou lentilles de Fresnel.
Augustin Fresnel est mort à 39 ans. Malgré la brièveté de sa vie, l'excellence et l'importance de ses travaux ont tout de suite été reconnues par ses contemporains. Il a été élu membre de l'Académie des sciences de Paris en 1823, membre associé de la Royal Society en 1825 et a reçu la médaille Rumford sur son lit de mort en 1827. Humphrey Loyd, professeur de physique au Trinity College à Dublin, considérait que la théorie ondulatoire de Fresnel était « la plus noble invention qui ait jamais honoré le domaine des sciences physiques, à la seule exception du système de l'Univers de Newton[1]. »
Famille
[modifier | modifier le code]Augustin Jean Fresnel est né à Broglie en Normandie le , fils de Jacques Fresnel (1755-1805), architecte, et d'Augustine Mérimée (1755-1833). Augustin a un frère aîné et deux frères cadets. Louis (1786-1809) qui sera admis à l'École polytechnique, deviendra lieutenant d'artillerie et sera tué à Jaca en Espagne la veille de son 23e anniversaire. Léonor (1790-1869) deviendra ingénieur des Ponts et Chaussées et succédera à Augustin à la Commission des phares. Il est le seul des frères Fresnel à s'être marié. Fulgence (1795-1855) deviendra linguiste, diplomate et orientaliste.

Augustin Fresnel a été très influencé par sa famille maternelle. Il était le petit fils de François Mérimée, avocat au parlement de Rouen, intendant du maréchal de Broglie. Il était filleul de son oncle Léonor Mérimée (1757-1836), le père de l'écrivain Prosper Mérimée, qui était "élève à l'Académie royale de peinture" au moment de son baptême[2]. C'est donc cet oncle-parrain qui l'a soutenu après la mort de son père en 1805. À cette époque, Léonor Mérimée cesse son activité d'artiste peintre pour se consacrer à l'étude de l'histoire et des techniques de peinture. Il est directeur de l'École des Beaux-Arts et professeur de dessin à l'École polytechnique. C'est lui qui mettra en relation son neveu avec François Arago au moment l'élaboration de la théorie de la diffraction de la lumière en 1815.
La famille Fresnel était très liée à la famille de Broglie[3]. Il est très probable que Jacques Fresnel, architecte, résidant à Broglie, était au service du maréchal de Broglie et que c'est au château qu'il a fait connaissance de la fille de l'intendant qui deviendra son épouse. Lors de la Révolution française, la famille de Broglie a émigré, le château a été pillé et incendié. Le prince Claude Victor de Broglie, fils aîné du maréchal, qui était député aux états généraux et avait choisi de rester en France, fut exécuté en 1794. La famille Fresnel s'est réfugiée d'abord à Cherbourg en 1790 puis, en 1794, à Mathieu, village natal de Jacques Fresnel, à quelques kilomètres au nord de Caen.
Un descendant du maréchal de Broglie, Louis de Broglie, proposera la théorie ondulatoire de la matière un siècle après que la théorie ondulatoire de la lumière eut été établie par Augustin Fresnel.
Éducation
[modifier | modifier le code]Augustine Mérimée était une pieuse catholique et même un peu janséniste[4]. Augustin Fresnel a donc passé son enfance et son adolescence dans une famille catholique et royaliste, marquée par les méfaits de la Révolution. Bien qu'il ait bénéficié des institutions nouvelles, l'École centrale de Caen et l'École polytechnique, il est resté, sa vie durant, royaliste et fervent catholique[5].
Selon Émile Verdet, au début de sa carrière, « ce n'est pas du côté de l'optique que se tournèrent d'abord ses pensées. Sous l'influence des souvenirs d'une éducation de famille où la religion avait tenu la première place, il commença à méditer sur les questions philosophiques et s'efforça de trouver une démonstration scientifique et rigoureuse de la vérité de quelques-unes des croyances qui avaient été jadis pour lui l'objet de la foi la plus ardente[6]. »
Arago rapporte que « Madame Mérimée était douée des plus heureuses qualités du cœur et de l'esprit ; l'instruction solide et variée qu'elle avait reçue dans sa jeunesse lui permit de s'associer activement pendant huit années consécutives aux efforts que faisait son mari pour l'éducation de leurs quatre enfants. Les progrès du fils ainé furent brillants et rapides. Augustin, au contraire, avançait dans ses études avec une extrême lenteur; à huit ans, il savait à peine lire[7]. » Il semble qu'Augustin était réticent à faire des efforts de mémoire. « Il n'eut jamais aucun goût pour l'étude des langues » rapporte Arago. Mais était très friand des exercices de raisonnement, dans les sciences ou dans la pratique. Ses camarades lui avait attribué le qualificatif d'homme de génie car il était très doué pour choisir les branches d'arbres les plus adaptées pour construire des arcs et des flèches ou d'autres objets[8]. On peut penser que l'influence de son père, architecte, a été décisive d'une part sur le développement de ses connaissances en arithmétique et en géométrie, qui lui ont permis d'entrer au collège sans difficulté et d'y briller, et d'autre part sur sa capacité à penser et dessiner dans l'espace, manifeste dans ses études ultérieures sur la diffraction et la polarisation de la lumière.
En 1801, à 13 ans, Augustin rejoint son frère Louis à l’École centrale de Caen. À 16 ans et demi, il est admis à l’École polytechnique (promotion 1804). Il a des professeurs de mathématiques très compétents : Siméon-Denis Poisson, Gaspard Monge, Adrien-Marie Legendre et un répétiteur, André-Marie Ampère[9],[10]. Par contre, l'enseignement de physique à l'École polytechnique était très médiocre. « Fresnel n'avait pu y trouver aucune notion tant soit peu exacte des travaux de ses devanciers sur la théorie des ondes[11] ». Il a cependant dû être instruit de la théorie de Newton sur la lumière qu'il s'appliquera à démolir. En 1814, il fait l'acquisition du Traité élémentaire de physique de René Just Haüy pour compléter ses connaissances[12].
En 1806, il devient élève de l’École des ponts et chaussées. Là, il apprend la topographie. Il fait partie de la génération des Arpenteurs du monde[13]. Fresnel a arpenté méticuleusement les chemins de la lumière avec le savoir-faire qu'il a acquis à l'École des ponts. Il a fait des mesures précises de distance et d'angle et a toujours estimé la marge d'erreur dont elles étaient grevées. Il sort de l'École en 1809 avec le titre et l'emploi d'ingénieur ordinaire aspirant du Corps des Ponts et Chaussées. Il restera toute sa vie dans cette administration[14],[6].
La vie de Fresnel est entièrement consacrée à sa profession et à ses recherches scientifiques. Il consacre une part de ses revenus pour acheter les instruments dont il a besoin pour ses recherches. « Les émoluments des deux positions occupées par Fresnel, ceux d'ingénieur et d'académicien auraient amplement suffi à ses modestes désirs, si le besoin des recherches scientifiques n'avaient pas été chez lui une seconde nature ; la construction et l'achat d'instruments délicats sans lesquels aujourd'hui, on ne saurait, en physique, rien produire d'exact, absorbait tous les ans une partie de son patrimoine[15]. »
Affectations successives
[modifier | modifier le code]Cent-jours
[modifier | modifier le code]La Vendée fut le premier département où Fresnel fut affecté pour participer à l'édification de Napoléon-ville (La Roche-sur-Yon)[16]. C'est là qu'en 1811 il inventa une méthode de production industrielle de soude, que l'on connait aujourd'hui sous le nom de procédé Solvay. Sa découverte fut présentée aux chimistes compétents par l'intermédiaire de son oncle Léonor mais elle ne fut pas retenue car, à la différence de celle de Solvay, elle ne comprenait pas le recyclage de l'ammoniaque, ce qui la rendait économiquement sans intérêt[17],[18].
Vers 1812, Fresnel fut envoyé à Nyons, dans la Drôme, sur le chantier de la route impériale qui devait relier l'Italie à l'Espagne[16]. C'est à Nyons qu'il manifeste son intérêt pour l'optique. Le , il écrit en post-scriptum à une lettre à son frère Léonor :
- « Je voudrais bien avoir aussi des mémoires qui me missent au fait des découvertes des physiciens français sur la polarisation de la lumière. J'ai vu dans Le Moniteur, il y a quelques mois, que Biot avait lu à l'Institut un mémoire fort intéressant sur le polarisation de la lumière[19]. J'ai beau me casser la tête, je ne devine pas ce que c'est »[20].

Plus tard, il manifeste son intérêt pour la théorie ondulatoire de la lumière qui, à son avis, expliquerait la constance de la vitesse de la lumière et serait compatible avec l'aberration stellaire. Finalement, il rassemble ses idées dans un texte qu'il intitule Rêveries et qu'il envoie à son oncle Léonor Mérimée qui le transmet à André-Marie Ampère. Le , Léonor Mérimée évoque la note de Fresnel au cours d'un dîner avec Ampère et Arago, professeurs comme lui à Polytechnique. François Arago n'a que 2 ans de plus qu'Augustin Fresnel. Il est entré à l'École Polytechnique en 1803 en même temps que son frère Louis. Il se comportera à son égard comme un frère, tantôt protecteur, tantôt collaborateur. Ampère, Arago et Fresnel formeront un trio amical et scientifiquement fécond.
En mars 1815, Fresnel perçoit le retour de Napoléon de l'île d'Elbe comme "une attaque contre la civilisation"[21]. Il quitte son poste et se rend à Lapalud dans le Vaucluse où il offre ses services à la résistance royale mais il n'est pas pris à cause de son apparence chétive. « Fresnel rentra à Nyons, presque mourant... La populace lui fit subir mille outrages » dit Arago[22]. Il est arrêté à Valence le 8 mai 1815. Il est relâché mais est destitué pendant les Cent-jours tout en ayant l'autorisation de se rendre chez sa mère à Mathieu. « Fresnel obtint la permission de passer par Paris. Il put renouer connaissance avec d'anciens condisciples et se préparer ainsi aux recherches scientifiques dont il comptait s'occuper dans la retraite où ses jeunes années s'étaient écoulées[22] ». Le 12 juillet, alors que Fresnel est sur le départ, Arago lui laisse une note dans laquelle il attire son attention sur la diffraction de la lumière :
- « Je ne connais pas d'ouvrage qui renferme la totalité des expériences que les physiciens ont faites sur la diffraction de la lumière. Monsieur Fresnel ne pourra se mettre au courant de cette partie de l'optique qu'en lisant l'ouvrage de Grimaldi, celui de Newton, le traité anglais de Jordan et les Mémoires de Brougham et de Young, qui font partie de la collection des Transactions philosophiques[23] ».
Fresnel n'a pas accès à ces publications en dehors de Paris et ne parle pas anglais[24]. Malgré ces difficultés, arrivé à Mathieu, il entreprend des expériences sur la diffraction et les interférences de la lumière[25],[26]. Ces loisirs forcés rappellent ceux de Newton à Woolsthorpe au moment de la grande peste de Londres en 1665 : ils sont l'occasion de grandes intuitions. Le , Napoléon abdique définitivement. Fresnel a 27 ans. Il est réintégré dans le Corps des Ponts et Chaussées puisqu'il a choisi le camp qui l'a finalement emporté. Il demande immédiatement une prolongation de son congé de deux mois pour finir son travail. Ce qui lui est accordé, les travaux publics ayant été suspendus partout pendant la période de trouble occasionné par le retour de Napoléon[27].
Le 23 septembre, il écrit à Arago : « Je pense que j'ai trouvé l'explication et la loi des franges colorées que l'on remarque dans l'ombre des corps éclairés par un point lumineux. » Cependant, dans le même paragraphe, Fresnel doute implicitement de la nouveauté de sa découverte. Il lui faudrait engager quelques dépenses pour améliorer son équipement. Il veut savoir si ces travaux sont inutiles ou si la loi de la diffraction n'a pas déjà été établie avec des expériences plus précises que les siennes. Il explique qu'il n'a pas encore eu l'occasion d'acquérir les ouvrages de sa liste de lecture à l'exception du livre de Young qu'il ne peut pas comprendre sans l'aide de son frère[28].
Fresnel conclut son travail de trois mois et envoie, le 15 octobre, un manuscrit intitulé Mémoire sur la diffraction de la lumière à Delambre, secrétaire perpétuel de l'Institut, par l'intermédiaire de son oncle. Arago, qui a pris connaissance du Mémoire, lui écrit le 8 novembre. Fresnel lui répond le [29]. Il est ennuyé. Il voudrait savoir plus précisément en quoi il a répété ou contredit les travaux de Young. Il annonce que son congé se termine et qu'il doit rejoindre Rennes. Le , il écrit encore de Mathieu pour décrire les expériences complémentaires qu'il a faites sur les franges extérieures pour satisfaire la demande d'Arago.
Rennes
[modifier | modifier le code]Le , Fresnel écrit de Rennes. Il fait des commentaires et des corrections sur son Mémoire. Il remercie Arago des démarches qu'il a entreprises auprès de Gaspard de Prony, directeur de l'École des Ponts, pour que Fresnel vienne quelque temps à Paris pour finaliser son travail. Arago a fait valoir que cela serait favorable au progrès de la science et au prestige du Corps des Ponts et Chaussées. Prony a relayé la demande auprès Louis-Mathieu Molé, directeur du Corps des Ponts, supérieur hiérarchique de Fresnel. Fresnel pourra venir à Paris dès février 1816 et faire des expériences complémentaires avec Arago.
L'année 1816 fut une année sans été : les récoltes furent maigres. Les familles affamées formaient des queues dans les rues de Rennes. Le gouvernement fut obligé d'organiser des ateliers de charité pour les nécessiteux. En octobre, Fresnel est renvoyé en Ille-et-Vilaine pour superviser ces ateliers en plus de ses équipes ordinaires de cantonniers[30]. Selon Arago :
- « Chez Fresnel, l'homme consciencieux marchait toujours en première ligne; aussi s'acquitta-t-il constamment de ses devoirs d'ingénieur avec le plus rigoureux scrupule. La mission de défendre les deniers de l'Etat, d'en obtenir le meilleur emploi possible, se présentait à ses yeux comme une question d'honneur. Le fonctionnaire, quel que fût son rang, qui lui soumettait un compte louche devenait à l'instant l'objet de son profond mépris. Dans ces circonstances, la douceur habituelle de ses manières disparaissait, pour faire place à une raideur, je dirai même à une âpreté qui, dans ce siècle de concessions, lui attira de nombreux désagréments[31] ».
Les lettres de Fresnel de montrent son anxiété constante. Il se plaint à Arago d'être « tourmenté par les ennuis de la surveillance et la nécessité de réprimander. » A Mérimée, il écrit : « Je ne trouve rien de plus fatigant que d'avoir à diriger des hommes et j'admets que je n'ai aucune idée de ce que je fais[32] ».
Paris
[modifier | modifier le code]À l'automne 1817, Fresnel, soutenu par Prony, obtient un nouveau congé de son supérieur hiérarchique, Louis Becquey, et rentre à Paris[33],[34]. Il reprendra son poste d'ingénieur au printemps 1818 mais, à Paris, cette fois, d'abord au canal de l'Ourcq[33] et ensuite, à partir de mai 1819, au cadastre des rues de Paris[35],[36]. Le , il est nommé à la Commission des phares. L'entretien des phares français faisait partie des missions du Corps des Ponts.
Durant ses séjours à Paris, Fresnel est hébergé par son oncle Léonor Mérimée. À partir de 1822, il loue une chambre chez Ampère, dans la maison qu'il a achetée en 1818, au no 19, rue des Fossés-Saint-Victor, à l'emplacement du no 55, rue du Cardinal-Lemoine, aujourd'hui. Dans cette maison, Ampère avait aménagé un petit laboratoire pour faire ses expériences sur les interactions entre électricité et magnétisme, expériences auxquelles Fresnel a participé depuis 1820, Ampère étant génial théoricien mais pauvre expérimentateur alors que Fresnel était à la fois théoricien et expérimentateur talentueux[37].
Diffraction
[modifier | modifier le code]Premier mémoire sur la diffraction de la lumière
[modifier | modifier le code]Lumière et chaleur
[modifier | modifier le code]Fresnel commence son exposé par des considérations sur la lumière et le calorique. Il constate que, quand la lumière éclaire un corps noir, celui-ci se réchauffe et, bien qu'il n'émette pas de lumière, il émet du calorique. Il en déduit que « les molécules lumineuses et les molécules caloriques sont de même nature[38]. » Il néglige la transmission de chaleur par conduction qui a fait l'objet des travaux de Joseph Fourier et que l'Académie refuse de publier depuis 1808. Mais son intuition rejoint les observations de William Herschel qui, en 1800, a découvert qu'il existe des rayons thermiques ou calorifiques à une extrémité du spectre : les rayons infra-rouges qui sont effectivement de même nature que la lumière.
Théorie de Newton
[modifier | modifier le code]Fresnel s'attache ensuite à démontrer les insuffisances et les incohérences de la théorie de l'émission de Newton[39].
- Newton pensait que la vitesse de déplacement des corpuscules de lumière détermine leur couleur.
- « Les accès de facile réflexion et facile transmission sont à peu près inexplicables dans le système de Newton. »
- « La double réfraction a obligé Newton de faire encore une nouvelle hypothèse, qui est bien extraordinaire : c'est que les molécules lumineuses ont des pôles et que le Spath d'Islande tourne d'un même côté les pôles de même espèce. »
- Il conclut : « Il me semble que la théorie des vibrations se plie mieux que celle de Newton à tous les phénomènes […] La plus forte objection qu'on ait faite à cette théorie est celle qui est fondée sur la comparaison de la lumière et du son […] La marche de la lumière est infiniment plus rapide que celle de l'air ; son mouvement doit donc se répandre beaucoup moins [que le son] en dehors de sa direction primitive, tant qu'aucun obstacle ne le dérange ; car la lumière, par la rencontre d'un corps, peut être réfléchie comme le son, réfractée ou infléchie. Cette objection, la seule à laquelle il me paraisse difficile de répondre complètement, m'a conduit à m'occuper des ombres portées. » Voilà le problème posé.
Dispositif expérimental
[modifier | modifier le code]Fresnel est chez sa mère à Mathieu. À part quelques loupes, il ne dispose d'aucun instrument. Il les construit avec les moyens disponibles.
- La source lumineuse — Suivant l'expérience de Newton, il utilise la lumière du soleil qu'il laisse filtrer à travers une ouverture dans un volet. « Je me suis d'abord servi, pour obtenir un point lumineux, d'un très petit trou fait dans une feuille d'étain, sur laquelle je rassemblais beaucoup de lumière au moyen d'une grande lentille. Mais le mouvement du soleil déplaçait promptement le foyer, et chaque observation ne pouvait durer qu'un instant […] N'ayant pas de plus forte lentille, pour obtenir un point lumineux plus fin, je me suis servi d'un globule de miel déposé sur un petit trou fait à une feuille de cuivre[40]. »
- L'obstacle — « Eclairé par ce globule, le fil de fer, dont je mesurais les franges, en produisait encore de très nettes, même lorsqu'il n'était plus qu'à un centimètre du point lumineux »
- Le banc optique idéal qu'il décrit au conditionnel et qu'il a réalisé au mieux avec l'aide du serrurier du village, écrit Verdet : une grande règle graduée en cuivre sur laquelle il place une lentille qui focalise la lumière, un fil ou un ruban étroit vertical, une lentille, un écran blanc en carton et/ou un micromètre[40].
- L'écran — « N'ayant pas de micromètre, je me suis d'abord servi du premier moyen. Je recevais l'ombre sur un carton blanc et je mesurais la distance entre les deux franges extérieures du premier ordre, en prenant dans chaque frange, le point où cesse le rouge et où le violet commence[41]. »
- Le micromètre — « J'ai construit moi-même un micromètre avec lequel je puis mesurer les largeurs des ombres à moins d'un quarantième de millimètre près. Il est formé de deux fils de soie partant d'un même point et aboutissant à deux points éloignés l'un de l'autre de cinq millimètres[...] Un petit carton mobile me sert à marquer l'endroit où la distance entre les fils est égale à la largeur de l'ombre[42]. »
Résultats
[modifier | modifier le code]Franges extérieures
[modifier | modifier le code]Fresnel considère que les franges extérieures à l'ombre portée (en EG sur la figure) résultent de la superposition des rayons directs issus de la source et des rayons réfléchis par le bord de l'obstacle. La réflexion des ondes par le bord de l'obstacle est une hypothèse inexacte héritée de Newton et que Fresnel corrigera par la suite. Pour effectuer ses calculs, Fresnel prend SE comme axe des abscisses et Sy' comme axe des ordonnées.
- « J'ai considéré le point lumineux et les deux bords du fil comme des centres d'ondulations régulières, et les intersections de leurs cercles devaient me donner la position des franges. J'ai trouvé, pour l'expression de la distance de la première frange extérieure au bord de l'ombre, telle qu'elle serait sans la diffraction : , a, représentant la distance du point lumineux au fil, b, celle du fil au carton sur lequel on reçoit l'ombre, et , la longueur d'une ondulation[43]. »
Une des grandes difficultés de ses expériences est l'usage de la lumière blanche qui fait que les franges de différentes longueurs d'onde se chevauchent. Il fait ses mesures sur la limite entre les franges rouges du premier ordre et les franges violettes du second ordre et, pour les calculs, prend nm comme longueur d'onde moyenne. Il obtient des résultats en accord raisonnable avec les observations à condition de supposer que l'onde réfléchie sur le bord de l'obstacle est inversée par rapport à l'onde incidente (différence de chemin de ). Il remarque aussi que
- « Une conséquence très remarquable de cette théorie de la diffraction, c'est que la même frange ne se propage pas en ligne droite, mais suivant une hyperbole, dont les foyers sont le point lumineux et un des bords du fil [...] La différence entre les deux rayons vecteurs étant presque égale à la distance entre les deux foyers, l'hyperbole se rapproche extrêmement d'une ligne droite et c'est ce qui a été cause de l'erreur où est tombée Newton[44]. »
En effet, Newton a considéré que les franges se déplaçaient en ligne droite.
Franges intérieures
[modifier | modifier le code]Fresnel s'intéresse ensuite aux franges qui se forment à l'intérieur de l'ombre et s'aperçoit qu'elles disparaissent quand il ajoute une feuille de papier sur un côté du fil. Il écrit :
- « Dès que je me suis occupé des franges intérieures, j'ai fait sur le champ cette réflexion : puisqu'en interceptant la lumière d'un côté du fil, on fait disparaitre les franges intérieures, le concours des rayons qui arrivent des deux côtés est donc nécessaire à leur production[...] C'est la rencontre, le croisement même de ces rayons qui produit les franges. Cette conséquence, qui n'est pour ainsi dire que la traduction du phénomène, est tout à fait opposée à l'hypothèse de Newton et confirme la théorie des vibrations. On conçoit aisément que les vibrations de deux rayons, qui se croisent sous un très petit angle, peuvent se contrarier lorsque les nœuds des unes répondent aux ventres des autres[45]. »
On peut remarquer que son vocabulaire n'est pas encore au point car il emploie les termes de nœuds et de ventres, qui concernent les ondes stationnaires, ce qui n'est pas le cas dans le phénomène des interférences. Mais il semble raisonner juste puisqu'il indique que les franges sombres correspondent aux zones de superposition d'ondes qui diffèrent d'une demie longueur d'onde, qui sont donc en opposition de phase.

Pour trouver la formule qui donne la distance entre les franges, il fait une construction géométrique en traçant les cercles centrés au bord de l'obstacle et de rayons successifs augmentés d'une demie longueur d'onde[46]. Si S est la source, O, l'axe du fil de fer vu en coupe et l'origine du repère cartésien xOy, , le diamètre du fil de fer, la distance , la distance , x et y les coordonnées du point Q d'observation sur l'écran, les équations des cercles centrés en A ou en B s'écrivent :
En Q, intersection des deux cercles centrés en A et en B, se forme une frange sombre sombre du premier ordre. On peut reporter la valeur de obtenue dans une équation, dans l'autre. De plus, comme , le terme en peut être négligé. D'où il résulte :
Étant donné que , la distance d'une frange à l'axe des abscisses, Fresnel en déduit que la distance entre les deux franges sombres du premier ordre est deux fois plus grande, soit . L'écart entre celles du deuxième ordre est , entre celles du troisième ordre, . Dans un tableau comparatif, il montre que les mesures effectuées corroborent le résultat des calculs[47].
Fresnel note que « la distance entre les franges intérieures est indépendante de celle du fil au point lumineux. » Cependant, il fait une autre observation. Quand il remplace le fil par un ruban opaque large comme le diamètre du fil et qu'il le fait tourner autour de la direction de l'axe du fil précédemment installé, il constate que la disposition des franges n'est pas perturbée bien que la distance AQ s'allonge en A'Q et que BQ se raccourcisse en B'Q. Fresnel en déduit que ce qui importe n'est pas la différence des chemins AQ et BQ, mais la différence des chemins depuis la source, SAQ et SBQ. Pour qu'il y ait interférence, il faut que les vibrations vibrent en accord depuis la source[48].
Fresnel a donc traité les bords de l'obstacle comme deux sources ponctuelles cohérentes. Il a reproduit avec cet autre dispositif, l'expérience des doubles fentes que Young avait conduite 15 ans plus tôt et a retrouvé les mêmes résultats. Il a cependant prouvé que, avec la théorie ondulatoire, il pouvait expliquer le phénomène de la diffraction.
Remarques sur la réflexion, la réfraction et la polarisation
[modifier | modifier le code]Fresnel suggère que les lois ordinaires de la réflexion et de la réfraction peuvent aussi être expliquées en termes d'interférences. Il note que si deux rayons parallèles très proches sont réfléchis à des angles autres que ceux prévus par les lois de l'optique géométrique, ils n'auraient plus la même phase et s'annuleraient. Il indique que cette explication est valide tant que les irrégularités de surfaces sont beaucoup plus petites que la longueur d'onde.
Il fait le même type de démonstration pour les rayons réfractés par un dioptre et en déduit que « la marche de la lumière est plus lente dans le verre que dans l'air, suivant le rapport du sinus de réfraction à celui d'incidence. » Ce qui est une conséquence absolument opposée à la théorie de Newton[49]. D'après Emile Verdet « Ce qui appartient en propre à Fresnel et dont on n'aperçoit aucune trace chez ses devanciers, c'est l'idée féconde d'expliquer les lois de la réflexion et de la réfraction par le principe des interférences[50]. »
Fresnel discute ensuite de l'interprétation des anneaux de Newton à la lumière de la théorie ondulatoire, sans pouvoir conclure. Pour terminer, il revient à sa question initiale de 1814 :
- « Cette théorie des vibrations et de l'influence des rayons les uns sur les autres, qui lie déjà tant de phénomènes séparés dans celle de Newton, ne doit-elle pas conduire à la véritable explication de la polarisation[51] ? »
Devenir du Mémoire
[modifier | modifier le code]Le , Fresnel écrit à Arago pour avoir des nouvelles de son manuscrit : « Je désirerais bien savoir quel jugement vous en portez. Votre suffrage est celui que j'ambitionne le plus. » Après avoir résumé les grandes lignes de son Mémoire, il écrit qu'il est probable que la théorie des vibrations et des interférences « doit conduire aussi à une explication satisfaisante de la double réfraction et de la polarisation. C'est actuellement l'objet de mes recherches. » Il conclut en demandant à Arago de lui envoyer le tableau de données sur la polarisation, publiées récemment par Biot, pour qu'il puisse travailler dessus[52].
Le 8 novembre, Arago lui répond :
- « J'ai été chargé par l'Institut de l'examen de votre mémoire sur la diffraction de la lumière. Je l'ai étudié avec soin et j'y ai trouvé un grand nombre d'expériences intéressantes, dont quelques-unes avaient déjà été faites par le docteur Thomas Young qui, en général, envisage ce phénomène de manière analogue à celle que vous avez adoptée. Mais ce que, ni lui, ni personne n'avait vu avant vous, c'est que les bandes colorées extérieures ne cheminent pas en ligne droite à mesure qu'on s'éloigne du corps opaque. Les résultats que vous avez obtenus à cet égard me semblent très importants. Peut-être pourront-ils servir à prouver la vérité du système des ondulations si souvent, et si faiblement combattus par des physiciens qui ne s'étaient pas donné la peine de le comprendre. Vous pouvez compter sur l'empressement que je mettrai à faire valoir votre expérience : la conséquence qui s'en déduit est tellement opposée au système à la mode, que je dois m'attendre à beaucoup d'objections[53] ».
Arago termine sa lettre en l'encourageant à ne pas se disperser : « Je ne vous envoie pas par ce courrier les renseignements que vous me demandez sur les phénomènes de polarisation, de peur que de nouvelles recherches ne vous fasse abandonner la diffraction, que je désire, pour mille raisons, vous voir suivre encore quelques jours[54]. »
Nouvelles expériences à Paris avec Arago
[modifier | modifier le code]Fresnel est revenu à Paris en février 1816 pour faire des expériences complémentaires avec Arago. L'une d'entre elles sera communiquée le , en séance de l'Institut sous forme d'une "Note sur un phénomène remarquable qui s'observe dans la diffraction de la lumière". Dans cette communication, Arago rapporte une expérience de diffraction par un fil dans laquelle, selon la prédiction de Fresnel, les franges internes sont déplacées si les rayons d'un côté de l'obstacle passent à travers une fine lame de verre. Fresnel a attribué correctement ce phénomène au fait que la vitesse de la lumière est plus faible dans le verre que dans l'air[55].
Version finale du premier Mémoire sur la diffraction
[modifier | modifier le code]Finalement, une version corrigée et enrichie est présentée à l'Académie par Arago, le 25 mars 1816[56]. Intitulé Mémoire sur la diffraction de la lumière, où l'on examine particulièrement le phénomène des franges colorées que présentent les ombres des corps éclairés par un point lumineux, il est publié dans le numéro de mars 1816 (paru en mai) des Annales de Chimie et de Physique dont Arago est devenu récemment le co-éditeur[57]. Il est reproduit dans les Œuvres complètes sous le titre Deuxième Mémoire[58].
Par rapport au premier manuscrit déposé à l'Académie, la publication comporte beaucoup d'expériences et de mesures qui ont été refaites avec Arago à Paris en utilisant de la lumière monochromatique rouge ( nm). Fresnel essaie d'expliquer comment la lumière s'infléchit au bord d'un obstacle ? La dispersion de la lumière varierait-elle avec la courbure de l'arête ? « C'est ce qui n'a pas lieu de manière sensible du moins dans le voisinage de l'ombre, puisque le dos et le tranchant d'un rasoir donnent des franges d'un égal éclat. L'hypothèse la plus naturelle, c'est que les molécules du corps mise en vibration par la lumière incidente deviennent les centres de nouvelles ondulations. » Il se rapproche de la conception des ondelettes secondaires de Huygens qu'il cite pour la première fois[59].
Fresnel remarque que « les rayons qui ont été obscurcis par la discordance de leurs vibrations redeviennent lumineux ensuite dans la partie du trajet où les ondulations sont d'accord, et qu'ainsi ils peuvent reprendre leur éclat après l'avoir perdu momentanément[60]. » Le résultat de l'interférence des ondes est transitoire et localisé dans l'espace et le temps. Les ondes poursuivent leur chemin, en se superposant, si on ne les arrête pas sur un écran d'observation.
En mars, Fresnel a déjà des compétiteurs : Biot présente un mémoire sur la diffraction dont il est l'auteur avec son étudiant Claude Pouillet, mémoire qui prétend que la régularité des franges de diffraction, comme celle des anneaux de Newton, doit être liée aux "ajustements" de Newton. Mais la démonstration n'est pas rigoureuse et Pouillet lui-même deviendra un des premiers défenseurs de la théorie ondulatoire[61],[62].
Supplément au premier Mémoire sur la diffraction
[modifier | modifier le code]Trois semaines après avoir envoyé son premier Mémoire, le 10 novembre, Fresnel (qui est toujours à Mathieu) envoie à l'Académie un Supplément au premier Mémoire sur la diffraction de la lumière[63].
Diffraction par les réseaux
[modifier | modifier le code]Il note en particulier que, si une surface polie contient des rayures, il y a diffusion et non réflexion de la lumière. Les règles de la réflexion ne s'appliquent pas. Pour que les ondes de deux rayons parallèles très proches s'additionnent, il faut que la différence de chemin soit égale à une longueur d'onde, soit

i étant l'angle d'incidence, r, l'angle de réflexion (ici de dispersion) et n, un nombre entier. L'angle de réflexion dépendra donc de la couleur. Si l'on grave un grand nombre de rayures équidistantes de sur la surface, la lumière sera dispersée en couleurs différentes « rangées dans le même ordre que dans le spectre solaire. » Fresnel invente donc le réseau de diffraction qui sera découvert quelques années plus tard par son contemporain et collègue bavarois Joseph von Fraunhofer qui mourra un an avant lui, et comme lui, de tuberculose. Dans sa note, il rapporte aussi ses observations de la diffraction de la lumière par transmission à travers les fibres d'un tissu[64].
Anneaux de Newton
[modifier | modifier le code]
Les anneaux sombres se répètent ensuite dans chaque zone où la distance entre le miroir plan et le ménisque est égale à un nombre entier de demies longueurs d'onde, provoquant des différences de chemin (aller et retour) égales à un nombre entier de longueurs d'onde. Avec cette théorie, il rend compte parfaitement du tableau de données effectuées par Newton. Il montre ensuite que la théorie explique l'apparence inversée des anneaux vus par transmission : là où il y a de l'ombre par réflexion, il y a de la lumière par transmission. En effet, la double réflexion introduit deux inversions de phase, ce qui rend l'onde transmise directement (BB') et l'onde deux fois réfléchie (r3) déphasées d'une longueur d'onde, donc en accord[65]. Fresnel expose son interprétation de la formation des anneaux colorés par la théorie ondulatoire. Rappelons que les anneaux de Newton se forment lorsqu'une lentille plan-convexe de très faible courbure repose sur un dioptre plan en verre. En incidence normale, par réflexion, les anneaux sombres doivent correspondre à l'addition de deux ondes décalées d'une demie longueur d'onde, c'est-à-dire à une annulation de l'onde réfléchie par la première interface (r1), par l'onde réfléchie par la seconde interface (r2). Au centre, qui apparait sombre, l'onde réfléchie par la lentille interfère avec l'onde réfléchie par le miroir plan. Comme la différence de chemin parcouru est nulle, c'est qu'une des deux réflexions provoque une inversion de phase. Fresnel avoue qu'il ne sait pas si c'est la première ou la seconde mais il affirme que le phénomène se produit et qu'il explique les interférences qui provoquent les anneaux.

Fresnel explique aussi la loi de répartition des anneaux sous incidence oblique. « Ainsi l'épaisseur de la lame d'air qui réfléchit un anneau dans une direction oblique est égale à celle de la lame d'air qui réfléchit le même anneau perpendiculairement à sa surface, divisée par le cosinus de l'angle d'incidence dans l'air. » Et là encore, il trouve une parfaite concordance entre ses calculs et les mesures effectuées par Newton[66].
Publication du Supplément au premier Mémoire
[modifier | modifier le code]Le , Fresnel écrit (en français) à Young, reconnaissant qu'une grande partie de son mémoire n'est pas original[67],[68].
Le Supplément au premier Mémoire sur la diffraction de la lumière est présenté à l'académie le par Arago[69]. Fresnel commence par présenter, en les réfutant, les hypothèses de Newton sur les anneaux colorés. Il présente ensuite sa propre interprétation du phénomène telle quelle a été exposée plus haut[70] et qu'il résume :
- « Il est bien plus naturel de supposer que ce sont les rayons réfléchis par le verre plan qui modifie ceux que renvoie la seconde surface de la lentille, qu'ils se fortifient mutuellement lorsque leurs vibrations s'accordent et se détruisent, ou du moins s'affaiblissent beaucoup, quand leurs vibrations se contrarient. Ainsi l'influence des rayons lumineux les uns sur les autres, démontrée par les phénomènes de la diffraction, l'est encore par les anneaux colorés[71]. »

Fresnel explique pourquoi sa démonstration concernant les anneaux colorés n'a pas été publiée dans le premier Mémoire :
- « Mr Arago m'ayant appris que le Dr Young avait déjà donné depuis longtemps la même explication du phénomène. Comme elle est peu connue, j'ai pensé qu'il était utile de la présenter de nouveau dans ce second Mémoire où je me suis proposé de faire sentir les avantages du système des vibrations, en le comparant à celui de Newton. J'ai d'ailleurs quelques explications nouvelles à ajouter à cette théorie et ce que je viens de dire était nécessaire à leur intelligence[73]. »
Il rapporte ensuite deux expériences nouvelles et une nouvelle approche théorique : la diffraction par une fente lumineuse, les interférences obtenues par les images d'une fente lumineuse par deux miroirs et la diffraction par un petit objet opaque.
Expérience du miroir double
[modifier | modifier le code]
Fresnel décrit l'expérience du double miroir (miroirs de Fresnel) comprenant deux miroirs plans juxtaposés en formant un angle d'un peu moins de 180°, avec lequel il produit une image d'interférence à partir de deux images virtuelles de la même fente source. Une expérience avec une double fente nécessitait une première fente source pour s'assurer que la lumière qui parvenait aux deux fentes était cohérente. Dans le dispositif de Fresnel, l'unique première fente est maintenue et les deux fentes secondaires sont remplacées par le double miroir qui n'a aucune ressemblance physique avec les doubles fentes et remplit cependant la même fonction. Ce résultat, qui avait été annoncé par Arago dans le numéro de mars des Annales, rendait difficile de croire que le résultat des doubles fentes avait quoi que ce soit à voir avec des corpuscules déviés par les bords des fentes (ce qui était la théorie de Newton)[74].
Figure de diffraction d'une fente lumineuse
[modifier | modifier le code]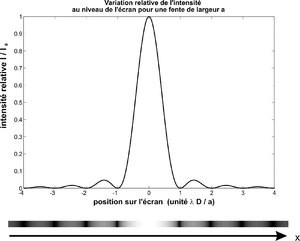
Fresnel refait l'expérience, rapportée par Biot, de la diffraction de la lumière par une fente étroite. Il ne trouve pas la même chose et découvre la loi de répartition des franges. Il appelle b la distance de la fente (ou diaphragme) à l'écran d'observation, c, la largeur de la fente et λ, la longueur d'onde.
- « La distance entre les points les plus sombres de deux bandes consécutives, prises à droite ou à gauche de l'intervalle clair du milieu, était égale à bλ/c, ou du moins en différait assez peu. Quant à l'intervalle du milieu, j'ai trouvé qu'il variait entre deux limites bλ/c et 2bλ/c, suivant une loi que je n'ai pas encore pu déterminer.
- Lorsque le diaphragme est très étroit, et qu'on en reçoit l'ombre à une distance assez considérable, l'intervalle du milieu est toujours, à très peu près, le double des autres intervalles[75]. »
Mécanismes de la diffraction
[modifier | modifier le code]« On trouve pour la première fois exposées dans ce Mémoire les causes mécaniques vraies de la diffraction, mais l'auteur n'était pas encore parvenu, à cette époque, à résoudre toutes les difficultés que présentait la théorie dans son application aux phénomènes ». (Note d'Émile Verdet[76])
Franges intérieures
[modifier | modifier le code]Fresnel examine ce qui se passe au niveau du front d'onde au voisinage du bord de l'obstacle AF (Fig.7). Il inverse sa construction géométrique par rapport à la Fig.1. A n'est plus le point à partir duquel sont mesurées les distances au point d'observation Q. C'est à partir du point Q que sont mesurées les distances au bord de l'obstacle. Il trace des rayons QA, QC = QA + λ / 2, QD = QA + 2λ / 2, QE = QA + 3λ / 2... qui délimitent des zones sur la surface du front d'onde, les zones de Fresnel. Il remarque que les rayons issus de l'arc AC sont en opposition de phase avec les rayons issus de l'arc CD. Ils devraient donc en grande partie se neutraliser. Mais les rayons de l'arc CD sont eux-mêmes en opposition de phase avec ceux de l'arc DE. Et ainsi de suite lorsqu'on parcourt le front d'onde au-delà de AE.

Fresnel en déduit que tous les rayons arrivant en Q et issus du front d'onde se neutralisent à l'exception de ceux qui sont issus de l'arc AC : « excepté cet arc extrême, chaque partie de l'onde directe se trouve comprise entre deux autres qui détruisent les rayons obliques qu'elle tend à produire. C'est donc le milieu B de l'arc AC qui doit être considéré comme le centre principal des ondulations qui se font sentir au point Q »[77]. Il considère que le rayon QB qu'il nomme le rayon efficace est de longueur QA + λ / 4, ce qui fait que, contrairement à ce qu'il affirme, il n'est pas strictement au milieu de l'arc AC. Il conclut son raisonnement en affirmant que le point B doit être considéré comme la véritable origine des rayons qui arrivent au point Q. Et que c'est le point G, et non le point F, qui doit être pris pour origine des rayons émanant de l'autre côté de l'obstacle. Ces considérations ne changent pas les calculs de position des franges internes présentés dans son premier mémoire, étant donné que les chemins optiques sont augmentés de la même valeur (λ / 4) des deux côtés.
Franges extérieures
[modifier | modifier le code]« On prouverait par un raisonnement semblable que, lorsque les rayons s'infléchissent hors de l'ombre, le rayon efficace est plus court d'un quart d'ondulation que celui qui partirait du corps. » Ainsi, à la sortie de l'ombre, la différence de chemin entre les deux rayons efficaces PB et PG augmente plus rapidement que celle entre les deux rayons PA et PF et à une certaine distance de la limite de l'ombre, la différence de chemin atteint λ / 2. Cependant, les franges externes ne résultent pas de la superposition des ondes issues des deux côtés de l'obstacle mais de la superposition du rayon efficace et du rayon direct. La différence de chemin ne serait que de λ/4. La nouvelle théorie ne marche pas pour les franges externes[78].
Deuxième Mémoire sur la diffraction de la lumière
[modifier | modifier le code]Le , l'Académie des sciences annonce que la diffraction de la lumière sera le thème du prochain Grand Prix biannuel de physique qui sera attribué en 1819[79]. La date limite de soumission des manuscrits est fixée au de façon que le jury ait le temps de répéter les expériences proposées. Bien que l'énoncé du sujet parle de rayons et d'inflexion, il ne mentionne pas la possibilité de mettre en œuvre une théorie ondulatoire. Arago et Ampère encouragent Fresnel à participer au concours[80].
Composition de deux fonctions sinusoïdales
[modifier | modifier le code]Le , dans une note additionnelle à un article sur la polarisation[81], Fresnel établit l'équation des ondes lumineuses sous forme de fonctions sinusoïdales. Il pose :
Il prend en compte la longueur d'ondulation, c'est-à-dire la longueur d'onde, mais semble ignorer le terme de fréquence (). Tout en restant au plus proche de son expression, nous posons :
Il pose que l'équation d'une onde de même longueur d'onde qui aurait parcouru un chemin plus long que la première doit être :
Avec , la différence de marche de l'onde 2 par rapport à l'onde 1.
Il fait remarquer que, lorsque d = λ/4, les deux ondes ont des positions orthogonales, c'est-à-dire qu'elles sont déphasées de π/2 et que la résultante des deux ondes peut être calculée comme la résultante de deux forces perpendiculaires. Lorsque d est quelconque, « l'onde résultant du concours des deux autres, quelles que soient leur positions relatives, répond exactement, pour son intensité et pour sa situation, à la résultante de deux forces égales aux intensités des deux faisceaux lumineux, et faisant entre elles un angle qui soit à la circonférence entière comme l'intervalle qui sépare les deux systèmes d'ondes est à la longueur d'une ondulation[82] ».
Le concept de vecteurs n'existait pas encore. Sa méthode sera désignée par la suite comme celle des Vecteurs de Fresnel. Il propose de décomposer chaque vecteur en ses composantes orthogonales rapportées à un système de coordonnées cartésiennes dont l'axe des abscisses est porté par le vecteur représentant l'onde directe.
Diffraction par un bord rectiligne
[modifier | modifier le code]La connaissance de cette méthode est assumée dans une note préliminaire, datée du et déposée le , dans laquelle Fresnel esquisse une théorie élémentaire de la diffraction telle qu'elle est décrite aujourd'hui dans les manuels de physique[83]. Il reformule le principe de Huygens en combinaison avec le Principe de superposition, affirmant que la vibration à chaque point d'un front d'onde est la somme des vibrations qui seraient envoyées en ce point à cet instant par tous les éléments du front d'onde dans n'importe laquelle de ses positions antérieures, tous les éléments agissant séparément selon le Principe de Huygens-Fresnel. Dans le cas d'un front d'onde partiellement occulté à une position antérieure, la somme doit être faite sur toute la partie non-occultée. Dans toutes les directions autres que la normale au front d'onde primaire, les ondes secondaires sont affaiblies à cause de l'inclinaison et encore plus affaiblies par les interférences destructives, si bien que l'effet de l'inclinaison seule peut être ignorée.[84],[85]. Pour la diffraction par un bord droit, l'intensité en fonction de la distance au bord de l'ombre géométrique peut alors être exprimée avec suffisamment d'exactitude par ce qu'on appelle maintenant les intégrales de Fresnel normalisées :

- et
La même note comprend un tableau des intégrales, avec la limite supérieure de 0 à 5.1 par incréments de 0.1, calculées avec une erreur moyenne de 0.0003, et un tableau plus petit des maxima et des minima de l'intensité résultante[86].

Dans son Mémoire sur la diffraction de la lumière déposé le et portant l'épigraphe latine Natura simplex et fecunda (La nature est simple et fertile), Fresnel augmente légèrement les deux tableaux sans changer les figures existantes, sauf pour une correction du premier minimum d'intensité. Pour être complet, il reprend sa solution du problème des interférences, où il traite la superposition des fonctions sinusoïdales comme l'addition de vecteurs. Il reconnait la directionnalisé des sources secondaires et la variation de leurs distances du point d'observation principalement pour expliquer pourquoi ces paramètres n'ont que peu d'importance, pourvu que la propagation des ondes secondaires ne soit pas rétrograde. Ensuite, appliquant sa théorie des interférences aux ondes secondaires, il exprime l'intensité de la lumière diffractée par le bord rectiligne d'un écran en termes d'intégrales qui incluent les dimensions du dispositif mais qui peuvent être normalisées comme précédemment. En référence aux intégrales, il explique le calcul des maxima et des minima d'intensité lumineuse (franges extérieures) et souligne que l'intensité chute très rapidement quand on va vers l'ombre géométrique[87]. Le dernier résultat, comme le dit Olivier Darrigol, revient à prouver la propagation rectiligne de la lumière dans le cadre de la théorie ondulatoire, la première preuve que la physique moderne accepte encore[88].
Pour vérifier expérimentalement ses calculs, Fresnel utilise une lumière rouge dont il déduit la longueur d'onde (638 nm) à partir du diagramme de diffraction d'un dispositif où la lumière incidente sur une fente unique est focalisée par une lentille cylindrique. En variant la distance de la source à l'obstacle et de l'obstacle au point d'observation, il compare les valeurs calculées et les positions observées des franges obtenues par un écran demi-plan, une fente, une bande étroite, en se concentrant sur la position des minima, plus faciles à localiser que les maxima de lumière. Pour la fente et la bande, il ne peut pas utiliser les tableaux de maxima et minima qu'il avait établis précédemment. Pour chaque combinaison de dimensions, l'intensité doit être exprimée en termes de sommes ou de différences des intégrales de Fresnel et calculée à partir du tableau des intégrales. Les extréma doivent être recalculés[89],[90]. Les écarts entre les positions calculées et les positions observées étaient inférieurs à 1.5 %[91].
Vers la fin de son mémoire, Fresnel résume les différences entre l'usage des ondes secondaires par Huygens et par lui : Huygens dit qu'il y a de la lumière seulement là où les ondes secondaires concordent, Fresnel dit qu'il y a complète obscurité seulement là où les ondes secondaires s'annihilent[92].
Tache de Poisson
[modifier | modifier le code]
Le jury du concours est composé de Laplace, Biot et Poisson (tous tenant de la théorie corpusculaire newtonienne), Gay-Lussac (neutre), et Arago qui, à la fin, écrit le rapport du jury[93],[94]. Bien que les soumissions soient en principe anonymes, le rapport de Fresnel était identifiable par son contenu[95]. De toute façon, il n'y a eu qu'une seule autre soumission dont ni le manuscrit ni l'auteur n'ont laissé de trace. L'existence de cette autre soumission est mentionnée seulement dans le dernier paragraphe du rapport du jury[96] et indique que l'auteur ignore les travaux précédents de Young et de Fresnel, utilise des méthodes d'observation insuffisamment précises, néglige certaines choses et commet des erreurs manifestes. Selon les mots de John Worrall, « La compétition à laquelle devait faire face Fresnel pouvait difficilement être moins sérieuse »[97]. On peut en déduire que le jury avait deux options : donner le prix à Fresnel ou ne pas l'attribuer.

L'examen du jury dura jusqu'à l'année suivante. C'est alors que Poisson, exploitant un cas où la théorie de Fresnel donnait des intégrales faciles, trouva que la théorie prédisait l'existence d'un point lumineux au centre de l'ombre projetée d'un petit disque éclairé par une source ponctuelle. Ceci semblait être une preuve par l'absurde que la théorie de Fresnel était fausse. Arago, intrigué par la démonstration de Poisson, réalisa l'expérience avec un disque opaque de 2 mm de diamètre et observa que, effectivement, une tache claire apparaissait au centre de l'ombre[98] ,[99],[100].
Le jury unanime accorda le Grand Prix au mémoire portant la sentence Natura simplex et fecunda au cours de la séance de l'Académie du 15 mars 1819[101]. Après l'annonce, le président de séance ouvrit une enveloppe cachetée accompagnant le mémoire et révéla que l'auteur était Augustin Fresnel[102]. Le résultat fut officiellement annoncé à une réunion publique de l'Académie une semaine plus tard, le 22 mars.
La vérification par Arago de la prédiction contre-intuitive de Poisson est passée dans l'histoire comme étant à l'origine de la décision d'attribution du prix[103],[104]. Cette façon de voir les choses n'est pas confirmée par le rapport du jury qui ne consacre à l'épisode que deux phrases dans l'avant dernier paragraphe. La version imprimée du rapport fait aussi référence à une note (E), mais cette note concerne des recherches qui ont été faites "après" la décision d'attribution du prix [105]. Selon Kipnis [106], la signification réelle de la tache de Poisson et de son complément (le centre de la tache lumineuse projetée par une ouverture circulaire) est qu'elle concerne les intensités des franges, tandis que les mesures de Fresnel concernent les positions des franges. Mais, comme le note aussi Kipnis, cette question a été abordée seulement après que le prix ait été attribué.
Le triomphe de Fresnel n'a pas converti immédiatement Laplace, Biot et Poisson à la théorie ondulatoire pour au moins trois raisons :
- d'abord, il était possible d'interpréter les intégrales de Fresnel comme des règles de combinaison des rayons lumineux. Arago encourageait même cette interprétation, probablement pour minimiser la résistance aux idées de Fresnel[107],[98]. Même Biot a commencé à enseigner le principe de Huygens-Fresnel sans s'engager pour autant vis à vis de la théorie ondulatoire[106] ;
- ensuite, la théorie de Fresnel n'expliquait pas vraiment le mécanisme de la génération des ondes secondaires ni pourquoi elles avaient une diffusion angulaire significative. Cela ennuyait particulièrement Poisson[108],[109] ;
- enfin, la question qui intéressait le plus les physiciens de l'optique à ce moment-là n'était pas la diffraction mais la polarisation de la lumière, phénomène sur lequel Fresnel travaillait mais n'était pas encore en mesure d'apporter une explication originale.
Polarisation
[modifier | modifier le code]Histoire
[modifier | modifier le code]En 1669, le danois Rasmus Bartholin découvre qu'un cristal de spath d'Islande (calcite transparente) donne une double image d'un texte sur lequel il est posé. Les propriétés optiques étranges de ce minéral intrigue les savants. Christiaan Huygens les étudient avec soin et publie ses observations dans son Traité de la lumière en 1690. La capacité de la lumière à donner deux faisceaux dans certaines circonstances, comme si la lumière était attirée dans un sens ou dans un autre, est nommée polarisation par Newton. L'énigme de la lumière polarisée reste entière pendant un siècle jusqu'à ce qu’Étienne Louis Malus fasse une découverte fortuite[110].

En 1808, alors qu'il observe le Palais du Luxembourg à Paris à travers un cristal de calcite, Malus constate que la lumière du soleil réfléchie par les vitres est plus ou moins éteinte selon l'orientation du cristal. Il en déduit que la réflexion de la lumière sur la surface d'un corps transparent provoque sa polarisation. Malus garde les conceptions de Newton sur la nature de la lumière. Pour interpréter la polarisation, il ajoute un caractère orienté aux molécules de lumière, orientation aléatoire dans un plan perpendiculaire à la direction de propagation[111].
En 1811, Arago découvre la rotation du plan de polarisation. Lorsqu'il fait passer un faisceau de lumière polarisée par réflexion à travers une lame mince de quartz, convenablement taillée, la direction de polarisation tourne d'un certain angle autour de l'axe de propagation. L'année suivante, Biot met en évidence les rotations tantôt dextrogyre (vers la droite) tantôt lévogyre (vers la gauche) du plan de polarisation par des lames de quartz. En 1815, il observe que des corps organiques en solution peuvent aussi provoquer la rotation du plan de polarisation. Le même phénomène se produit lorsque la lumière polarisée traverse des gaz (vapeur d'essence de térébenthine)[112].
En 1815, David Brewster reprend les travaux de Malus (mort en 1812). Il étudie en détail la polarisation par réflexion. Il détermine l'« angle de polarisation », ou angle de Brewster, c'est-à-dire l'angle pour lequel les rayons réfléchis sont totalement polarisés. Pour cet angle, les rayons réfractés font un angle droit avec les rayons réfléchis et sont polarisés dans la direction perpendiculaire à celle des rayons réfléchis[110].
Interférence de la lumière polarisée - Polarisation chromatique (1816–1821)
[modifier | modifier le code]Dans une lettre du , Fresnel écrit : « Je ne sais pas ce qu'on entend par polarisation de la lumière. Priez, M. Mérimée, mon oncle, de m'envoyer les ouvrages dans lesquels je pourrai l'apprendre. »
Dans un mémoire écrit le et révisé le 6 octobre, Fresnel rapporte que, quand un cristal biréfringent produit deux images d'une seule fente, il ne peut pas faire interférer les deux faisceaux. Une expérience plus générale, suggérée par Arago, montre que si deux faisceaux issus d'une double fente sont polarisés séparément, l'image d'interférence apparait ou disparait lorsque le polariseur d'un des faisceaux est tourné, donnant une pleine interférence quand les deux polariseurs sont parallèles, et rien quand les polariseurs sont à angle droit [113], [114], [115] . Ceci contredisait l'hypothèse de "polarisation mobile" de Biot[116],[117].
Dans le même article, Fresnel faisait la première allusion à la théorie ondulatoire de la polarisation chromatique. Quand la lumière polarisée passe à travers une lame cristalline, elle est séparée en deux faisceaux, le faisceau ordinaire et le faisceau extraordinaire avec des intensités correspondant à la loi de Malus, qui sont polarisés perpendiculairement et ne peuvent interférer, et donc ne produisent aucune couleur d'interférence. Cependant, si les deux faisceaux passent à travers un second polariseur, leurs polarisations sont réalignées et ils peuvent interférer[114]. Cette explication, en elle-même, prédit que si l'analyseur est tourné de 90°, les faisceaux ordinaires et extraordinaires échangent leurs rôles si bien que si un analyseur a la forme d'un cristal de calcite, les deux images de la lame devraient avoir la même couleur (ceci sera revisité plus bas). Mais en fait, comme Arago et Biot l'avait trouvé, ils sont de couleurs complémentaires. Pour corriger sa prédiction, Fresnel proposa une règle d'inversion de phase par laquelle une des ondes constituantes de l'une des deux images subirait un déphasage de 180° en traversant la lame. Cette inversion était une faiblesse de la théorie par rapport à celle de Biot, comme l'a reconnu Fresnel[118], même si la règle précisait laquelle des deux images avait une phase inversée[119]. De plus, Fresnel ne pouvait expliquer que des situations particulières parce qu'il n'avait pas encore résolu le problème de la superposition des fonctions sinusoïdales avec des déphasages quelconques dus aux différences de vitesse de propagation dans la lame[120].
Il a résolu le problème dans un « supplément » signé le (mentionné ci-dessus). Dans le même article, il aménage la loi de Malus en proposant une loi sous-jacente : si la lumière polarisée est incidente sur un cristal biréfringent avec son axe optique formant un angle θ avec le "plan de polarisation", les vibrations ordinaires et extraordinaires (en fonction du temps) sont réglées par les facteurs et , respectivement. Bien que les lecteurs modernes interprètent aisément ces facteurs en termes de composants perpendiculaires d'une oscillation transversale, Fresnel ne les expliquait pas (encore) de cette façon. Il avait donc encore besoin de la règle d'inversion des phases. Il a appliqué tous ces principes à un cas de polarisation chromatique non couvert par la théorie de Biot, impliquant deux lames successives avec des axes à 45°, et a obtenu des résultats en désaccord avec les prédictions de Biot (sauf des cas spéciaux) mais en accord avec les siennes[121].
Fresnel a appliqué les mêmes principes au cas classique de polarisation chromatique dans lequel une lame biréfringente était fendue parallèlement à son axe et placée entre un polariseur et un analyseur. Si l'analyseur avait la forme d'un cristal épais de calcite avec son axe dans le plan de polarisation, Fresnel prédisait que les intensités des images ordinaires et extraordinaires de la lame seraient respectivement proportionnelles à :
où est l'angle entre le plan de polarisation initial et l'axe optique de la lame, est l'angle entre le plan de polarisation initial et le plan de polarisation de l'image finale ordinaire et est le retard de phase de l'onde extraordinaire par rapport à l'onde ordinaire due à la différence de temps de propagation à travers la lame. Les termes en sont des termes dépendant de la fréquence et expliquent pourquoi la lame doit être mince pour produire des couleurs discernables : si la lame est trop épaisse, passera à travers trop de cycles quand la fréquence varie dans le spectre visible, et l'œil (qui divise le spectre visible en seulement trois bandes (correspondant aux trois espèces de cônes) ne sera pas capable de résoudre les cycles.
À partir de ces équations, on vérifie facilement que pour tout si bien que les couleurs sont complémentaires. Sans la règle d'inversion des phases, il y aurait un signe plus en face du dernier terme de la seconde équation de telle sorte que le terme dépendant de serait le même dans les deux équations, impliquant (de façon incorrecte) que les couleurs étaient identiques.
Ces équations étaient incluses dans une note non datée que Fresnel avait donnée à Biot[122] à laquelle Biot a ajouté quelques lignes de sa main. Dans le texte ci-dessus, φ est une abréviation pour 2π(e − o) chez Fresnel, où e et o sont les nombres de cycles parcourus respectivement par les rayons extraordinaires et ordinaires en traversant la lame. Si nous substituons
Alors les formules de Fresnel peuvent être réécrites
qui ne sont rien d'autre que les formules empiriques de Biot de 1812[123],[124] sauf que Biot interprétait et comme des sélections "non-affectées" et "affectées" des rayons incidents sur la lame. Si les substitutions de Biot étaient exactes, elles impliqueraient que ses résultats expérimentaux étaient mieux expliqués par la théorie de Fresnel que par la sienne.
Arago a retardé la publication du travail de Fresnel sur la polarisation chromatique jusqu'en juin 1821, quand il l'a utilisée pour une attaque globale contre la théorie de Biot. Dans sa réponse écrite, Biot protesta contre l'attaque d'Arago qui dépassait l'objectif principal du papier de Fresnel. Mais Biot déclara aussi que la substitution de et , et donc que les expressions de Fresnel pour et étaient empiriquement fausses parce que, quand les intensités des couleurs spectrales de Fresnel étaient définies selon les règles de Newton, le cosinus et le sinus carrés variaient trop lentement pour rendre compte de la séquence des couleurs observées. Cette affirmation suscita une réponse écrite de Fresnel qui contesta le caractère rapide du changement de couleur, remarquant que l'œil humain ne pouvait pas juger objectivement de ces variations de couleur. Fresnel fit aussi remarquer que différents observateurs pouvaient donner différents noms à une même couleur. De plus, affirma-t-il, un unique observateur ne peut comparer que des couleurs l'une à côté de l'autre, et que même s'il juge les couleurs égales, c'est une identité de sensation, pas forcément de composition. Biot a laissé sans réponse l'argument le plus ancien et le plus solide de Fresnel à savoir que les cristaux minces sont sujets à la même loi que les cristaux épais et ne nécessitent pas une théorie particulière. Il semble qu'Arago et Fresnel aient gagné le débat[125],[126],[127],[128].
À ce moment-là, Fresnel avait trouvé une nouvelle explication, plus simple, de ses équations de la polarisation chromatique.
Ondes transversales (1821)
[modifier | modifier le code]
Dans un manuscrit du , Fresnel mentionne deux hypothèses, dont l'une est attribuée à Ampère, selon lesquelles l'impossibilité de faire interférer des faisceaux polarisés perpendiculairement pourrait être expliquée si les ondes lumineuses étaient en partie transversales. Mais Fresnel ne pouvait pas développer ces idées en une théorie globale. Dès septembre 1816[129], il réalisa que la non-interférence des faisceaux polarisés orthogonalement et la règle d'inversion de phase de la polarisation chromatique seraient plus facilement expliquées si les ondes étaient totalement transversales. Ampère a eu la même idée. Mais cela soulevait une autre difficulté : comme la lumière naturelle semblait non-polarisée et que ses ondes semblaient donc longitudinales, on avait besoin d'expliquer comment le composant longitudinal de la vibration disparaissait dans la polarisation et pourquoi il ne réapparaissait pas quand la lumière polarisée était réfléchie ou réfractée obliquement par une plaque de verre[130],[131],[132].
De façon indépendante, Young écrivit à Arago (en anglais) le : une vibration transversale constituerait une polarisation, et si deux ondes longitudinales se croisaient sous un angle suffisant, elles ne pourraient pas s'annuler sans laisser une vibration transversale résiduelle[133]. Young publia son idée dans un supplément de l' Encyclopædia Britannica en février 1818 dans lequel il ajouta que la loi de Malus serait expliquée si la polarisation consistait en une vibration transversale[134].
Fresnel, de son propre aveu, n'a probablement pas été le premier à suspecter que les ondes lumineuses auraient une composante transversale, ou que les ondes polarisées étaient exclusivement transversales. Et c'est Young, pas Fresnel, qui a été le premier à publier l'idée que la polarisation dépend de l'orientation d'une onde transversale. Mais ces théories incomplètes n'avaient pas réconcilié la nature de la polarisation avec l'existence apparente d'une lumière non-polarisée. C'est à Fresnel qu'on doit l'achèvement de la théorie.
Dans une note que Buchwald date de l'été 1818, Fresnel caresse l'idée que les ondes non-polarisées pourraient avoir la même énergie et la même inclinaison, avec des orientations distribuées uniformément autour de l'axe de propagation et que le degré de polarisation serait le degré de non-uniformité de la distribution. Deux pages plus loin, il note, apparemment pour la première fois par écrit, que sa règle d'inversion de phases et la non-interférence des rayons polarisés à 90° seraient facilement expliqués si les vibrations des rayons pleinement polarisés étaient perpendiculaires à la normale de l'onde, c'est-à-dire purement transversales[135],[136].
Mais s'il pouvait rendre compte du manque de polarisation en moyennant les composantes transversales, il n'avait pas non plus besoin d'assumer une composante longitudinale. Il suffisait de supposer que les ondes lumineuses sont purement transversales, donc toujours polarisées en ce sens qu'elles ont une orientation transversale particulière, et que l'état non-polarisé de la lumière naturelle ou directe est dû aux variations rapides et aléatoire de cette orientation. Dans ce cas, deux parties cohérentes de lumière non-polarisée interféreront parce que leurs orientations seront synchronisées.
On ne sait pas quand Fresnel a accompli ce dernier pas parce qu'il n'y a pas de documentation à ce sujet en 1820 ou 1821[137] (peut-être parce qu'il était trop occupé à la mise au point de son prototype de lanterne pour le phare de Cordouan). Mais il a publié l'idée pour la première fois dans une série d'articles sur Le calcul des teintes... dans les Annales de mai, juin et juillet 1821. Dans le premier article, Fresnel décrivait la lumière directe (non-polarisée) comme la succession rapide d'un système d'ondes polarisées dans toutes les directions[138],[139] et donnait ce qui est aujourd'hui l'explication de la polarisation chromatique, en termes d'analogie entre polarisation et résolution de forces dans un plan, mentionnant les ondes transversales seulement dans une note en bas de page. L'introduction des ondes transversales comme argument principal a dû attendre le second article dans lequel il révéla sa suspicion qu'Ampère et lui entretenaient depuis 1816, et la difficulté qu'elle soulevait[140],[141]. Il poursuit « C'est seulement depuis quelques mois que, méditant plus attentivement sur le sujet, j'ai reconnu qu'il est très probable que les mouvements oscillatoires des ondes lumineuses sont exécutés seulement selon le plan de ces ondes, que ce soit pour la lumière directe ou pour la lumière polarisée[142] ». Dans le même article, Fresnel fait mention d'une lettre de Young à Arago, datée du (et perdue avant 1866), dans laquelle Young suggérait que les ondes lumineuses pourraient être analogues aux ondes sur les ressorts étendus. Mais Fresnel n'était pas enthousiasmé par l'analogie parce qu’elle suggérait à la fois des ondes longitudinales et transversales et qu'elle était difficilement conciliable avec un milieu fluide[143],[144],[129].
Selon cette nouvelle approche, il écrit : « la polarisation consiste, non pas à créer des vibrations transversales, mais à les décomposer en deux directions perpendiculaires l'une par rapport à l'autre et à les séparer en deux composantes[145],[146]. »
Pendant que les sélectionnistes insistent pour interpréter les intégrales de diffraction de Fresnel en termes de rayons discrets, dénombrables, ils ne pouvaient pas faire de même avec sa théorie de la polarisation. Pour un sélectioniste, l'état de polarisation d'un faisceau concerne la distribution des orientations parmi la population des rayons, et cette distribution était présumée statique. Pour Fresnel, l'état de polarisation d'un faisceau concernait la variation d'un déplacement en fonction du temps. Ce déplacement pouvait être contraint mais pas statique et les rayons n'étaient que des constructions géométriques, pas des objets dénombrables. L'écart conceptuel entre la théorie ondulatoire et le sélectionisme était devenu infranchissable[147].
L'autre difficulté posée par les ondes purement transversales était l'implication apparente que l'éther était un fluide solide élastique sauf que, pas comme les autres solides élastiques, il était incapable de transmettre des ondes longitudinales. Fresnel, dans un effort pour montrer que les ondes transversales n'étaient pas absurdes, suggéra que l'éther était un fluide comprenant un réseau de molécules, dont les couches adjacentes résisteraient aux déplacements par glissement jusqu'à un certain point au-delà duquel elles iraient vers un nouvel équilibre. Un tel milieu, pensait-il, se comporterait comme un solide pour des déformations suffisamment petites mais comme un liquide parfait pour les déformations plus importantes. Au sujet des ondes longitudinales, il suggérait de plus que les couches offraient une résistance incomparablement plus grande à un changement d'espacement qu'à un glissement[148],[149],[129].
« La théorie ondulatoire était économe en assomption, mais sa dernière assomption était chère en crédulité. Cette hypothèse de M. Fresnel est au moins très ingénieuse et peut nous conduire à quelques calculs satisfaisants, mais elle est soutenue par une circonstance qui est très redoutable dans ses conséquences. Les substances sur lesquelles M. Savart a fait ses expériences étaient des solides ; et ce sont seulement aux solides qu'une telle résistance latérale a toujours été attribuée. Si bien que, si nous adoptons les distinctions posées par le ressusciteur de la théorie ondulatoire lui-même dans ses conférences, on peut en déduire que l'éther luminifère, présent dans tout l'espace et pénétrant presque toute substance, n'est pas seulement hautement élastique, il est aussi absolument solide[150] !!! »; Si cette assomption devait être largement retenue, son pouvoir explicatif devrait être convaincant.
Réflexion partielle (1821)
[modifier | modifier le code]Dans la seconde partie du Calcul des teintes (juin 1821), Fresnel supposait, par analogie avec les ondes sonores, que la densité de l'éther dans un milieu réfractant était inversement proportionnel au carré de la vitesse de l'onde, et par conséquent, directement proportionnelle au carré de l'indice de réfraction. Pour la réflexion et la réfraction à la surface d'un dioptre, Fresnel décomposait les vibrations transversales en deux composantes perpendiculaires, maintenant connues comme les composantes s et p qui sont respectivement normale et parallèles au plan d'incidence. Le s vient de l'allemand senkrecht, perpendiculaire (au plan d'incidence). Pour la composante s, Fresnel supposait que l'interaction entre les deux milieux était analogue à une collision élastique. Il a obtenu une formule pour ce que nous appelons maintenant réflectivité : le rapport de l'intensité réfléchie à l'intensité incidente. La réflectivité prédite était non nulle pour tous les angles[151],[152],[129].
La troisième partie (juillet 1821) était un court post-scriptum dans lequel Fresnel annonce qu'il a trouvé, par une solution mécanique, une formule de la réflectivité de la composante p, qui prédit que la réflectivité est nulle à l'angle de Brewster. La polarisation par réflexion était désormais maîtrisée, avec la condition que la direction de la vibration dans le modèle de Fresnel était perpendiculaire au plan de polarisation défini par Malus (Sur la controverse qui s'est ensuivie voir Plan de polarisation). La technologie de l'époque ne permettait pas de mesurer précisément la réflectivité des composantes s et p pour vérifier expérimentalement l'exactitude des formules de Fresnel à tous les angles d'incidence. Mais les formules pouvaient être réécrites sous forme de ce que nous appelons le coefficient de réflexion : le rapport de l'amplitude réfléchie à l'amplitude incidente. Ensuite, si le plan de polarisation des rayons incidents était à 45° du plan d'incidence, la tangente de l'angle correspondant des rayons réfléchis était calculable à partir du rapport des deux coefficients de réflexion, et cet angle pouvait être mesuré. Fresnel l'a mesuré pour de multiples angles d'incidence, pour le verre et l'eau, et l'accord entre les angles mesurés et les angles calculés était inférieur à 1,5° dans tous les cas[153],[154],[129].
Fresnel a donné les détails de la « solution mécanique » dans son mémoire lu à l'Académie des sciences le 7 janvier 1823[155]. La conservation de l'énergie était combinée avec la continuité des vibrations "tangentielles" à l'interface[156],[157].
Les formules résultantes pour les coefficients de réflexion et les réflectivités sont connues sous le nom d'équations de Fresnel. Les coefficients pour les polarisations s et p peuvent être écrit :
où et sont les angles d'incidence et de réfraction. Ces équations sont connues respectivement comme la loi des sinus de Fresnel et la loi des tangentes de Fresnel[158],[159] ,[160]. En permettant aux coefficients d'être des nombres complexes, Fresnel a même tenu compte des déphasages différents pour les composantes s et p résultant de la réflexion interne totale[161],[162],[163].
Ce succès inspira James MacCullagh et Augustin-Louis Cauchy, au début de 1836, à analyser la réflexion par les métaux en utilisant des équations de Fresnel avec un indice de réfraction complexe[164],[165]. La même méthode est applicable aux milieux opaques non-métalliques.
Polarisation circulaire et elliptique. Optique rotatoire (1822)
[modifier | modifier le code]
Dans un mémoire daté du , Fresnel emploie les termes de
- polarisation rectiligne dans le cas simple où les composantes du vecteur représentant la vibration sont en phase ou déphasées de
- polarisation circulaire dans le cas où ces composantes sont égales et déphasées de
- polarisation elliptique pour les autres cas où les deux composantes sont inégales, mais dans un rapport fixe, et dans un écart de phase également constant.
Il explique ensuite comment on peut comprendre la rotation optique comme une espèce de biréfringence. Une lumière polarisée linéairement peut être décomposée en deux composantes polarisées circulairement tournant en sens inverses. Si ces composantes voyagent à des vitesses légèrement différentes, la différence de phase entre elles, et donc la direction de polarisation de leur résultante rectiligne, variera continûment avec la distance[166].
Ces concepts demandaient une redéfinition de la distinction entre lumière polarisée et non polarisée. Avant Fresnel, on pensait que la polarisation pouvait changer d'orientation et que le pouvoir d'extinction maximal d'un analyseur indiquait le degré de polarisation de la lumière. La lumière qui avait été convertie d'une polarisation rectiligne en une polarisation circulaire ou elliptique (par exemple, en passant à travers une lame cristalline ou en subissant une réflexion totale) était décrite comme partiellement ou totalement dépolarisée puisqu'un analyseur ne pouvait plus l'éteindre complètement. Après Fresnel, les caractéristiques de la lumière polarisée étaient le rapport fixe de ses composantes perpendiculaires et l'angle constant de leur déphasage. Avec cette définition, une lumière polarisée circulairement ou elliptiquement est pleinement polarisée, même si elle ne peut pas être complètement éteinte par un analyseur. L'écart conceptuel entre le séparatisme et la théorie ondulatoire s'élargissait encore[167].
Rhomboèdre de Fresnel (1817–23)
[modifier | modifier le code]
Le trajet de la lumière est matérialisé en vert. La composante verticale p est parallèle au plan d'incidence, et la composante horizontale s est perpendiculaire au plan et parallèle à la surface d'incidence. Si la lumière incidente est polarisée linéairement, ses deux composantes sont en phase. Après la première réflexion, la composante p est en avance de π/4 sur la composante s. Après la deuxième réflexion, la différence de phase atteint π/2, si bien que la polarisation est elliptique avec ses axes en direction de s et p. Si la polarisation initiale est à 45° du plan d'incidence, s et p sont initialement de même amplitude, et la polarisation finale est circulaire.
En 1817, David Brewster découvre qu'une lumière polarisée est partiellement dépolarisée par une réflexion totale interne si elle était initialement polarisée à un angle aigu du plan d'incidence[168]. Fresnel redécouvre cet effet et l'explore en incluant une réflexion totale dans une expérience de polarisation chromatique. Avec l'aide de sa première théorie de la polarisation chromatique, il trouve que la lumière apparemment dépolarisée était un mélange de composantes parallèle et perpendiculaire au plan d'incidence, et que la réflexion totale introduit une différence de phase entre ces deux composantes. Le choix d'un angle d'incidence approprié (mais pas encore déterminé) donne une différence de phase de π/4. Deux réflexions successives sur les faces parallèles de deux prismes accolés produisent une différence de phase de π/2. Ces observations ont été rapportées dans un mémoire envoyé à l'académie le et lu en séance quinze jours plus tard. Une note marginale non datée indique que les deux prismes couplés originaux ont été remplacés par la suite par un simple parallélépipède en verre connu comme le rhomboèdre de Fresnel[169].
Dans le supplément à ce mémoire, daté de janvier 1818, qui contient la méthode de superposition des fonctions sinusoïdales et la redéfinition de la loi de Malus en termes d'amplitudes, Fresnel décrit sa découverte du fait que la rotation optique peut être reproduite par les deux prismes jumelés, suivis d'une lame biréfringente ordinaire taillée parallèlement à son axe, et qui est placée de telle sorte que son axe soit à 45° du plan de réflexion dans les prismes, et suivie d'un second bi-prisme à 90° du premier[170]. Dans un article du 30 mars 1818, Fresnel rapporte que, si la lumière polarisée est pleinement dépolarisée par le rhomboèdre de Fresnel, ses propriétés ne peuvent pas être modifiées davantage par un passage supplémentaire dans un milieu doté d'un pouvoir rotatoire[171].
Le rapprochement entre la rotation optique et la biréfringence a été exploitée à nouveau en 1822 dans un article sur la polarisation circulaire et elliptique[172]. Ceci a été suivi par une communication sur la réflexion, présentée en janvier 1823, dans laquelle Fresnel quantifiait les déphasages dans la réflexion totale, et calculait ainsi précisément l'angle que devait avoir le rhomboèdre pour convertir une polarisation linéaire en polarisation circulaire. Pour un indice de réfraction de 1,51, il y a deux solutions : 48,6° et 54,6° [173].
Biréfringence
[modifier | modifier le code]Commission des phares
[modifier | modifier le code]Le , Fresnel est nommé à la Commission des phares, sur recommandation d'Arago qui en est lui-même membre, pour examiner les améliorations possibles de leur portée. L'entretien des phares français faisait partie des missions du Corps des Ponts.
État des techniques
[modifier | modifier le code]Feux
[modifier | modifier le code]Au début du XIXe siècle, la lanterne des phares consiste en une lampe à huile dont la lumière est focalisée par un miroir métallique de forme parabolique. La lampe est constituée d'une mèche dans laquelle monte par capillarité de l'huile contenue dans un réservoir. Le combustible est un mélange de blanc de baleine, d'huile d'olive et d'huile de colza. Vers la fin de l'Empire, se pose la question de l'amélioration de la lanterne du phare de Cordouan dont la tour avait été rehaussée de 30 m entre 1782 et 1789 et munie du premier feu tournant à réflecteurs paraboliques.
En Angleterre, un opticien, Thomas Rogers, avait tenté de remplacer les miroirs paraboliques par des lentilles de verre. Ses lentilles (de 53 cm de diamètre et de 14 cm d'épaisseur) avait été installées d'abord sur le phare de Portland Bill en 1789, puis sur quatre ou cinq autres. Mais l'épaisseur du verre absorbait une partie importante de la lumière[174].
Lentilles à anneaux
[modifier | modifier le code]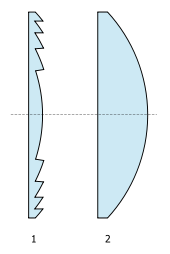
Le principe des lentilles à anneaux avait été proposé par Buffon en 1748 pour réduire le poids de la lentille et diminuer l'absorption de la lumière. Buffon envisageait de tailler et de polir directement un bloc de verre pour former sa lentille. Comme c'était pratiquement impossible, l'idée est restée sans application. Quarante ans plus tard, Condorcet reprend l'idée en suggérant qu'il serait peut-être possible de la réaliser en deux étapes : dans un premier temps la taille des éléments annulaires puis, dans un second temps, leur assemblage sur une armature. Mais cela dépassait encore les possibilités techniques de l'époque[175],[176].
Prototype
[modifier | modifier le code]
Fin août 1819, Fresnel propose à la commission de remplacer les miroirs paraboliques, qui ne transmettent que 50% de la lumière, par ce qu'il appelle des lentilles à échelons. C'est alors qu'un des membres de la commission, Jacques Charles, lui fait remarquer que le principe de ses lentilles avait déjà été imaginé par Buffon et Condorcet au siècle précédent. Fresnel, qui ignorait que sa découverte n'en était pas une, constate avec déception que « il a encore enfoncé une porte ouverte ». Cependant le modèle de Buffon était une lentille biconvexe d'une seule pièce tandis que celui de Fresnel est plan convexe et composé de multiples prismes beaucoup plus faciles à fabriquer. Le , Fresnel présente un projet plus abouti. La commission accorde un budget de 500 francs pour réaliser un prototype.
Après avoir approché divers artisans, Fresnel choisit François Soleil (1775-1846), opticien, et Bernard Henri Wagner (1790-1855), mécanicien horloger, avec lesquels les physiciens ont l'habitude de travailler pour construire leurs instruments d'expérimentation. Pendant que les artisans travaillent à la fabrication de l'optique, Fresnel et Arago se chargent de mettre au point une source lumineuse améliorée. Ils remplacent le mélange combustible par de la simple huile de colza. Au lieu de la laisser monter par capillarité dans les mèches, ils les alimentent par une pompe.
« Toutefois, cette application [les lentilles à échelons] n'aurait conduit à aucun résultat utile si on ne l'eut pas combinée avec des modifications convenables de la lampe, si la puissance de la flamme éclairante n'avait pas été considérablement augmentée. […] Fresnel et un de ses amis [Arago lui-même], s'y livrèrent avec ardeur et leur commun travail conduisit à une lampe à plusieurs mèches concentriques dont l'éclat égalait 25 fois celui des meilleures lampes à double courant d'air »[177].
Lorsque les 97 prismes nécessaires à la constitution d'une lentille sont réalisés, ils sont assemblés sur une vitre et collés entre eux avec de la colle de poisson pour former une lentille carrée. En mars 1820, la lentille de 76 cm de côté et 92 cm de focale est terminée et présentée à la commission[178]. La commission, très impressionnée, donne son feu vert pour la réalisation de sept autres lentilles. Un an plus tard, le système complet est terminé. « Les phares construits par Fresnel consistent en huit grands verres lenticulaires carrés, formant par leur réunion un prisme octogone dont le centre coïncide avec le foyer commun des lentilles ; en ce point est placée la lumière unique qui éclaire le phare ; elle est produite par un bec de lampe à trois mèches concentriques dans lequel un excès d'huile est injecté constamment par une pompe[179] ». L'appareil est présenté le en séance publique et comparé avec une lampe classique munie de réflecteurs paraboliques. La comparaison est sans appel[180].
Cordouan - Feu tournant
[modifier | modifier le code]
Après la démonstration de la validité du concept, Fresnel améliore encore son système. Les lentilles planes sont remplacées par des panneaux œil-de-bœufs faits d'arcs annulaires fabriqués par Saint-Gobain[181]. La rotation du système produit huit faisceaux tournants qui seront perçus par les marins comme des signaux périodiques. Au-dessus et à côté de chaque panneau, il installe d'autres petits œil-de-bœufs qui réfractent la lumière vers un miroir incliné de façon à réfléchir la lumière en un faisceau horizontal qui précède le faisceau principal. Ceci permet d'augmenter la durée de l'éclat[182].
En dessous des panneaux principaux, il place 128 petits miroirs arrangés en quatre cercles et superposés comme des stores vénitiens. Chaque cercle renvoie la lumière vers l'horizon, donnant une faible lumière constante entre les éclats. Le mécanisme de rotation du système est construit par Bernard Henri Wagner qui le dévoile au public à l'exposition des produits de l'industrie de 1823. Les pompes d'alimentation des lampes sortent aussi de l'atelier Wagner[183].
Le système complet est placé sur l'Arc de Triomphe non terminé et il est expérimenté le en présence de la commission, de Louis XVIII et de son entourage, à une distance de 32 km. L'appareil ainsi validé est acheminé et entreposé à Bordeaux pendant l'hiver. Il est installé à Cordouan sous la direction de Fresnel au printemps 1823. Le premier phare équipé de lentilles de Fresnel est mis en service le [184]. C'est à ce moment, que Fresnel commence à tousser et à cracher du sang. « Le phare de Fresnel a déjà eu pour juges, durant sept années consécutives, cette multitude de marins de tous les pays qui fréquentent le Golfe de Gascogne. Il a été étudié soigneusement sur place par de très habiles ingénieurs, venus tout exprès du Nord de l'Écosse avec une mission spéciale du gouvernement anglais. Je serai ici l'interprète des uns et des autres en affirmant que la France, où déjà l'importante invention des feux tournants avait pris naissance, possède maintenant, grâce aux travaux de notre savant confrère, les plus beaux phares de l'univers[185] ».
Dunkerque - Feu fixe
[modifier | modifier le code]
En mai 1824, Fresnel est promu secrétaire de la Commission des Phares, en devenant le premier membre rémunéré [186]. Il est aussi examinateur à l'École Polytechnique depuis 1821. Mais les longues heures de travail au moment de la saison des examens et son angoisse d'avoir à juger les autres le poussent à démissionner de ce poste à la fin 1824 pour concentrer son énergie sur l'installation de son mécanisme à Cordouan[187].
La même année, il dessine les premières lentilles fixes, pour diffuser la lumière uniformément sur l'horizon tout en minimisant la déperdition vers le haut et vers le bas. Les segments réfractant idéaux devraient être des segments de toroïde autour d'un axe vertical, de telle sorte que le panneau de dioptres ressemble à un tambour cylindrique. Si cela est additionné à des anneaux catadioptriques au dessus et en dessous de la partie dioptrique réfractive, le système complet ressemblerait à une ruche. Cependant, compte tenu de la difficulté à réaliser de grands prismes toroïdaux, l'appareil est réalisé avec 16 panneaux au lieu de huit. Il est mis en service à Dunkerque le [188].
En 1825, Fresnel complexifie son système de lentilles fixes en ajoutant un dispositif tournant à l'extérieur du système fixe pour réfracter une partie du faisceau fixe et le transformer en étroit pinceau tournant[189].
Cartes des phares
[modifier | modifier le code]En 1825 aussi, Fresnel dévoile sa Cartes de phares, décrivant un système de 51 phares et de feux portuaires plus petits à installer sur les côtes de France. Il classe les phares selon ce qu'il appelle des ordres. Les phares du premier ordre sont ceux qui ont la plus grande portée et sont dotés des plus grandes lentilles. Il propose aussi de systématiser un système d'identification des feux : lumière constante (système fixe), un éclat par minute (système tournant à 8 panneaux), deux éclats par minute (système tournant avec 16 panneaux)[190].
Fin 1825, Fresnel propose de remplacer les miroirs par des prismes à réflexion totale. Il en fait une version réduite qu'il installe sur le canal Saint-Martin. Mais il meurt avant d'en voir la réalisation en vraie grandeur. Pourtant, cette dernière amélioration donne aux lentilles de Fresnel l'aspect qu'elles ont encore de nos jours[191].

En conclusion, les lampes étant aux foyers des lentilles, les rayons émis du phare demeurent parallèles. En outre, les anneaux catadioptriques ajoutés autour des lentilles permettaient de ramener encore plus de flux vers le faisceau principal grâce à la réflexion totale ayant lieu à l'intérieur. La portée des phares ainsi équipés fut mesurée à 16 000 toises, soit environ 31,2 km. Le phare de Cordouan permit d'éclairer jusqu'à 11 lieues marines, alors que les phares à miroirs ne pouvaient jusque-là éclairer qu'à trois lieues[192].
Les phares du monde entier furent aussi rapidement équipés de lentilles de Fresnel, notamment, dans l'ordre[193]:
- 1823 : Angleterre
- 1824 : Espagne
- 1836 : Belgique
- 1837 : Italie
- 1840 : Suède
- 1841 : États-Unis
- 1845 : Prusse
- 1849 : Autriche
- 1850 : Brésil
- 1855 : Portugal et Turquie
- 1856 : Grèce.
La lentille de Fresnel est encore utilisée dans les phares maritimes, mais aussi dans les phares automobiles et les projecteurs de cinéma[194]. Des modèles souples bon marché permettant une vision grand angle sont réalisés aujourd'hui à partir de la lentille de Fresnel, ou les lentilles aux caisses de supermarché pour vérifier le contenu du chariot[195].
Honneurs, maladie et mort
[modifier | modifier le code]Fresnel était de constitution et de santé fragile. Son état de santé s'est détérioré pendant l'hiver 1822-1823 ce qui l'a empêché de rédiger un article sur la polarisation et la double réfraction que lui avait demandé l' Encyclopædia Britannica[196]. Les mémoires sur la polarisation circulaire et elliptique, sur la polarisation rotatoire ainsi que les détails de la dérivation des équations de Fresnel et leur application à la réflexion totale datent de cette période. Au printemps, il récupère suffisamment de force pour envisager de superviser l'installation des lentilles au phare de Cordouan. Mais il devient clair qu'il est atteint d'hémoptysie, c'est-à-dire de tuberculose[187]. En mai 1823, à sa troisième candidature, il est élu à l'unanimité membre de l'Académie des sciences. En 1824, il est fait chevalier dans l'ordre de la Légion d'honneur.
Cependant, comme sa santé se dégrade, on lui conseille de réduire son activité et de ménager ses forces. Considérant son travail sur les phares comme son devoir le plus important, il démissionne de sa fonction d'examinateur à l'École Polytechnique et ferme ses cahiers de recherche. Pourtant, le , il est élu membre étranger de la Royal Society. Dans sa dernière note à l'Académie, lue le , il décrit le premier radiomètre et attribue, à tort, les forces de répulsion à la température[197],[198],[199]. Bien que son travail de recherche soit arrêté, il continue à correspondre. En août ou septembre 1826, il trouve encore l'énergie pour répondre aux questions de John Herschel sur la théorie ondulatoire[200]. C'est Herschel qui recommande à la Royal Society d'accorder la médaille Rumford à Fresnel[201].

Pendant l'hiver 1826-1827, son état s'aggrave et l'empêche de retourner à Mathieu au printemps. La séance de l'Académie du 30 avril 1827 est la dernière à laquelle il assiste. Début juin on le transporte à Ville-d'Avray, 12 km à l'ouest de Paris. Sa mère vient le rejoindre. Il est assisté aussi par son collègue et ami Alphonse Duleau, comme lui ingénieur des Ponts et Chaussées. Celui-ci rapporte ces paroles de Fresnel :
- « J'eusse désiré vivre plus longtemps car je sens qu'il y a dans l'inépuisable carrière des sciences un grand nombre de questions d'utilité publique dont, peut-être, j'aurais eu le bonheur de trouver la solution[202]. »
Le 6 juillet, Arago vient lui remettre la médaille Rumford qui lui a été accordé "pour ses développements de la théorie ondulatoire appliquée aux phénomènes de la lumière polarisée et pour ses découvertes importantes et variées en optique physique".
- « Je vous remercie, me dit-il d'une voix éteinte, d'avoir accepté cette mission; je devine combien elle a dû vous coûter, car vous avez ressenti, n'est-ce pas, que la plus belle couronne est peu de chose quand il faut la déposer sur la tombe d'un ami[202]. »
Il meurt huit jours plus tard, le 14 juillet 1827. Augustin Fresnel est inhumé au cimetière du Père-Lachaise (14e division)[203]. Sa tombe porte l'inscription suivante "A la mémoire d'Augustin Jean Fresnel, membre de l'Institut de France".
Léonor Fresnel, polytechnicien et ingénieur du Corps des Ponts et Chaussée, est nommé à la Commission des phares où il succède à son frère Augustin et poursuit son œuvre[204].
Travaux de Fresnel
[modifier | modifier le code]- Augustin Fresnel, « Premier Mémoire sur la diffraction de la lumière », Annales de Chimie et de Physique Vol.1, , p. 239-281 (lire en ligne).
- Augustin Fresnel, « Mémoire sur les couleurs développées dans les fluides homogènes par la lumière polarisée », Académie des sciences réimprimé dans les Oeuvres de Fresnel Vol.1, (lire en ligne)
- François Arago et Augustin Fresnel, « Mémoire sur l'action que les rayons lumineux polarisés exercent les uns sur les autres », Annales de Chimie et de Physique Vol.10, , p. 288-306.
- Augustin Fresnel, « Mémoire sur la diffraction de la lumière », Mémoires de l'Académie royale des sciences, Vol.V, soumis le 29 juillet 1818, accepté le 15 mars 1819, publié en 1826, p. 339-475 (lire en ligne).

- Augustin Fresnel, De la lumière, contribution à l'ouvrage de Jean Riffault, Supplément à la traduction française de la cinquième édition du "Système de Chimie" par Th.Thomson, Paris, Méquignon - Marvis, , 547 p. réimprimé dans Œuvres complètes (1868), Vol.2, p. 3-146.
- Augustin Fresnel, « Mémoire sur un nouveau système d'éclairage des phares (suivi du Procès-verbal de l’expérience faite, le 20 août 1822 par la Commission des Phares, sur l’appareil lenticulaire à feux tournants destiné à l’éclairage du phare de Cordouan) », Académie royale des sciences réimprimé dans Oeuvres de Fresnel 1866-1870, Vol.3, , p. 97-126 (lire en ligne)
- Augustin Fresnel, « Mémoire sur la double réfraction », Mémoires de l'Académie Royale des Sciences de l'Institut de France Vol.7, , p. 45-176 (lire en ligne)
- H. de Senarmont, E.Verdet, and L.Fresnel, Oeuvres complètes d'Augustin Fresnel Vol.1, Paris, Imprimerie Impériale, , 804 p. (lire en ligne)
- H. de Senarmont, E.Verdet, and L.Fresnel, Oeuvres complètes d'Augustin Fresnel Vol.2, Paris, Imprimerie Impériale, , 854 p. (lire en ligne)
- H. de Senarmont, E.Verdet, and L.Fresnel, Oeuvres complètes d'Augustin Fresnel Vol.3, Paris, Imprimerie Impériale, , 844 p. (lire en ligne)
Hommages
[modifier | modifier le code]
- Son nom est inscrit sur la Tour Eiffel
- Le monument à Broglie à la mémoire d'Augustin Fresnel, édifié sur proposition du duc Albert de Broglie, a été inauguré le 14 septembre 1884.
- Plusieurs lycées portent son nom (à Paris, Caen, et Bernay dans l'Eure), le plus connu étant celui situé à Paris.
- Un sous-marin de la classe Pluviôse - lancé en 1908, et torpillé en 1915 - porte son nom, le Fresnel (Q65).
- Le 27 octobre 1927, l'Académie des sciences a célébré le centenaire de la mort d'Augustin Fresnel. Plusieurs académiciens français et étrangers lui ont rendu hommage[205].
- Un autre sous-marin - lancé en 1929, sabordé à Toulon en 1942, et coulé définitivement en 1944 - Fresnel (Q143) porte son nom.
- L’astéroïde (10111) Fresnel est nommé en son honneur.
- Un navire câblier lancé en 1997 porte son nom.
- En 2000, l'institut Fresnel est fondé à Marseille, résultant de la fusion de 3 laboratoires de recherche universitaires sur le campus de St Jérôme. L'institut Fresnel est une unité mixte de recherche d'Aix-Marseille université, l'école Centrale Marseille, et le CNRS.
Source
[modifier | modifier le code]- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Augustin-Jean Fresnel » (voir la liste des auteurs).
Notes et références
[modifier | modifier le code]- (en) H Lloyd, Lectures on the wave-theory of light. Part II. Lecture III, Dublin, Milliken, , p. 26
- Archives Départementales de l'Eure, « BMS (1751-1792) (8Mi872) », sur archives.eure.fr (consulté le )
- Cf. « Le château de Broglie, Eure », sur Maison de Broglie (consulté le ).
- (en) K.A. Kneller (traduction T.M. Kettle), Christianity and the Leaders of Modern Science: A contribution to the history of culture in the nineteenth century, Freiburg im Breisgau, Herder, (lire en ligne), p. 146-149
- (en) Henry Matthias Brock, « Augustin-Jean Fresnel », Catholic Encyclopedia Vol.6, (lire en ligne)
- Verdet, p. XXVIII.
- Arago 1830, p. 410.
- Arago 1830, p. 411.
- Michel Blay et Michèle Leduc, « Augustin Fresnel et la théorie ondulatoire de la lumière », voir Mourou et al., , p. 37-52
- Edmond Amouyal, « Ampère et Fresnel : lumière sur deux génies aux destins entremêlés », voir Mourou et al., , p. 55-78
- Verdet, p. XXIX.
- René Just Haüy, Traité élémentaire de Physique, Imprimerie Delance et Lesueur, (lire en ligne)
- Daniel Kehlmann, traduction par Juliette Aubert, Les arpenteurs du monde, Actes Sud, , 298 p.
- Arago 1830, p. 413.
- Arago 1830, p. 478.
- Fresnel O.C. 1866, p. XXVIII.
- (en) Jed Z. Buchwald, The Rise of the Wave Theory of Light: Optical Theory and Experiment in the Early Nineteenth Century, Chicago, University of Chicago Press, (ISBN 0-226-07886-8, lire en ligne), p. 113-114
- Fresnel 1830, p. 810-817.
- Jean-Baptiste Biot, « Mémoire sur une nouvelle application de la théorie des oscillations de la lumière », Lu en séance de la première classe de l'Institut,
- Verdet 1866, p. XXIX.
- Arago 1830, p. 416.
- Arago 1830, p. 417.
- Fresnel O.C. 1866, p. 6.
- Fresnel O.C. 1866, p. 6–7.
- (en) G. A. Boutry, « Augustin Fresnel: His time, life and work, 1788–1827 », Science Progress, vol. 36, no. 144, , p. 587–604
- Arago 1830, p. 418.
- (en) T.H. Levitt, A Short Bright Flash: Augustin Fresnel and the Birth of the Modern Lighthouse, New York, W.W. Norton, (ISBN 978-0-393-35089-0), p. 39
- (en) Thomas Young, A Course of Lectures on Natural Philosophy and the Mechanical Arts (2 volumes), London, J. Johnson,
- Fresnel 1866, p. 61-69.
- Levitt 2013, p. 43.
- Arago 1830, p. 415.
- Levitt 2013, p. 28, 237.
- Fresnel 1866, p. xxxv.
- Levitt 2013, p. 44.
- Fresnel 1866, p. xcvi.
- Arago 1830, p. 466.
- Edmond Amouyal, « Ampère et Fresnel : lumière sur deux génies aux destins entremêlés », in Mourou et al., , p. 55-78
- Fresnel O.C. 1866, p. 10.
- Tresnel O.C. 1866, p. 11-13.
- Fresnel O.C. 1866, p. 14.
- Fresnel O.C. 1866, p. 15.
- Fresnel O.C. 1866, p. 19.
- Fresnel O.C. 1866, p. 18.
- Fresnel O.C. 1866, p. 19-22.
- Fresnel O.C. 1866, p. 16-17.
- Fresnel O.C. 1866, p. 23-24.
- Fresnel O.C. 1866, p. 25.
- Fresnel O.C. 1866, p. 26.
- Fresnel O.C.1866, p. 28-31.
- Fresnel O.C. 1866.
- Fresnel O.C.1866, p. 33.
- Fresnel O.C. 1866, p. 35-38.
- Fresnel O.C. 1866, p. 38.
- Fresnel O.C. 1866, p. 39.
- Fresnel O.C. 1866, p. 75-77.
- Fresnel O.C. 1866, p. 78-87.
- Darrigol 2012, p. 201.
- Fresnel O.C. 1866, p. 89-122.
- Fresnel O.C. 1866, p. 118.
- Fresnel O.C. 1866, p. 112.
- (en) N. Kipnis, History of the principle of interference of light, Basel, Birkhäuser, (ISBN 978-3-0348-9717-4), p. 212-214 Chapitre VII & VIII
- (en) E. Frankel, « Corpuscular optics and the wave theory of light: the science and politics of a revolution in physics », Social Studies of Science Vol.6 n°2, , p. 141-184
- Fresnel O.C. 1866, p. 41-60.
- Fresnel O.C. 1866, p. 41-51.
- Fresnel O.C. 1866, p. 51-54.
- Fresnel O.C. 1866, p. 56-58.
- (en) Olivier Darrigol, A History of Optics: From Greek Antiquity to the Nineteenth Century, Oxford, Oxford University Press, , 327 p. (ISBN 978-0-19-964437-7), p. 201
- Young 1855, p. 376–378.
- Fresnel O.C. 1866, p. 129-170.
- Fresnel O.C. 1866, p. 133-142.
- Fresnel O.C. 1866, p. 134.
- Young, 1807, vol.1, p.777 & Fig.267.
- Fresnel O.C. 1866, p. 141.
- Fresnel O.C. 1866, p. 150-154.
- Fresnel O.C. 1866, p. 154-161.
- Fresnel O.C. et Vol.1 1866, p. 129.
- Fresnel O.C. 1866, p. 161-162.
- Fresnel 1866, p. 161-170.
- Darrigol 2012, p. 203.
- Buchwald 1989, p. 169–171.
- Fresnel O.C. 1866, p. 487-508.
- Fresnel O.C. 1866, p. 381.
- Fresnel 1866, p. 171–181.
- Fresnel 1866, p. 174–175.
- Buchwald 1989, p. 157–158.
- Buchwald 1989, p. 167.
- (en) Henry Crew, The wave theory of light. Memoirs by Huygens, Young and Fresnel, New York, American Book Company, , 192 p. (lire en ligne), pp. 101–108 (représentation vectorielle), 109 (pas de rayonnement rétrograde), 110–111 (directionnalité et distance), 118–122 (dérivation des intégrales), 124–125 (maxima & minima), 129–131 (ombre géométrique)
- Darrigol 2012, p. 204–205.
- Crew, 1900, p. 127–8 (longueur d'onde), 129–31 (demi-plan), 132–135 (extrema, fente)
- Fresnel 1866, p. 350-355.
- Buchwald 1989, p. 179–182.
- Crew 1900, p. 144.
- Buchwald 1989, p. 171,183.
- Levitt 2013, p. 45–46.
- Levitt 2013, p. 46.
- Fresnel O.C 1866, p. 236–237.
- (en) J. Worrall, Fresnel, Poisson and the white spot: The role of successful predictions in the acceptance of scientific theories, Cambridge University Press, in D. Gooding, T. Pinch, and S. Schaffer (eds.), The Uses of Experiment: Studies in the Natural Sciences, (ISBN 0-521-33185-4), p. 135-157
- Darrigol 2012, p. 205.
- Bernard Maitte, La lumière, Paris, Éditions du Seuil, coll. « Points Sciences », , 340 p. (ISBN 978-2-02-006034-9), « Crise et mutation de l'optique : l’œuvre de Fresnel », p. 226-227
- FresnelO.C. 186, p. 365-372.
- Worrall 1989, p. 140-141.
- Fresnel O.C. 1866, p. 230n.
- Worrall 1989, p. 135–138.
- Dominique Pestre, « La « tache de Poisson » fit triompher Fresnel », La Recherche, no 436, (lire en ligne)
- Worrall 1989, p. 143–146.
- Kipnis 1991, p. 221–222.
- Buchwald 1989, p. 183–184.
- Buchwald 1989, p. 186–198.
- Darrigol 2012, p. 205–206.
- Harris Benson, PHYSIQUE 3, Ondes, optique et physique moderne (3ème édition), Bruxelles, de Boeck, , 453 p. (ISBN 2-7613-1459-X), p. 221
- André Chappert, Etienne Louis Malus (1775-1812) et la théorie corpusculaire de la lumière, Paris, Librairie philosophique J. Vrin, (lire en ligne), p. 62
- Jeanne Crassous, « Fresnel vu par les chimistes. La biréfringence circulaire dans les milieux optiquement actifs », sur journals.openedition.org, (consulté le )
- Buchwald 1989, p. 203-205.
- Darrigol 2012, p. 206.
- Silliman 1967, p. 203–205.
- Darrigol 2012, p. 207.
- Frankel 1976, p. 163–164.
- Frankel 1976, p. 164.
- Buchwald 1989, p. 386.
- Buchwald 1989, p. 216.
- Buchwald 1989, p. 333–336.
- Fresnel O.C. 1866, p. 533–537.
- Buchwald 1989, p. 97.
- Frankel 1976, p. 148.
- Buchwald 1989, p. 237–251.
- Levitt 2009, p. 54–57.
- Frankel 1976, p. 165–168.
- Darrigol 2012, p. 208–209.
- Fresnel O.C. 1866, p. 609-648.
- Silliman 1967, p. 209–210.
- Buchwald 1989, p. 205–212.
- Fresnel O.C. 1866, p. 394n.
- Young 1855, p. 383.
- Young 1818, p. 333–335.
- Buchwald 1989, p. 225–226.
- Fresnel O.C. 1866, p. 526–527.
- Buchwald 1989, p. 226.
- Buchwald 1989, p. 227.
- Fresnel O.C. 1866, p. 612.
- Buchwald 1989, p. 212.
- Fresnel O.C. 1866, p. 629–630.
- Fresnel O.C. 1866, p. 630.
- Silliman 1967, p. 214–215.
- Fresnel O.C. 1866, p. 634–635.
- Buchwald 1989, p. 228.
- Fresnel O.C. 1866, p. 636.
- Buchwald 1989, p. 230.
- Silliman 1967, p. 216–218.
- Fresnel O.C. 1866, p. 630–634.
- Thomas Young (écrit en janvier 1823), Sect.XIII in "Refraction, double, and polarisation of light", Supplement to the Fourth, Fifth, and Sixth Editions of the Encyclopædia Britannica, vol.6 (1824), p.862, réimprimé dans Young, 1855, p.415 (points d'exclamation dans l'original)
- Buchwald 1989, p. 388–390.
- Fresnel O.C. 1866, p. 643.
- Buchwald 1989, p. 390–391.
- Fresnel O.C. 1866, p. 646–648.
- Fresnel 1823a.
- Buchwald 1989, p. 391–393.
- (en) E.T. Whittaker, A history of the theories of aether and electricity: From the age of Desvartes to the close of the nineteenth century, London, Longman, Green & Co,
- Whittaker 1910, p. 134.
- Darrigol 2012, p. 213.
- Fresnel O.C. 1866, p. 773.
- Buchwald 1989, p. 393–394.
- Whittaker 1910, p. 135–136.
- Fresnel O.C. 1866, p. 760–761.
- Whittaker 1910, p. 177–179.
- Buchwald 2013, p. 467.
- Buchwald 1989, p. 230–232.
- Buchwald 1989, p. 232.
- (en) David Brewster, « On a new species of moveable polarisation », [Quaterly] Journal os science and the Arts Vol.2 n°3, , p. 213
- Fresnel O.C. Vol.1, 1866, Mémoire sur les modifications que la réflexion imprime à la lumière polarisée, , p. 441-485
- Fresnel O.C. Vol.1, 1866, Supplément au Mémoire sur les modifications que la réflexion imprime à la lumière polarisée, , p. 487-508
- Fresnel O.C. Vol.1, 1866, Mémoire sur les couleurs développées dans les fluides homogènes par la lumière polarisée, , p. 655-683
- Fresnel O.C. Vol.1, 1866, Mémoire sur la double réfraction que les rayons lumineux éprouvent en traversant les aiguilles de cristal de roche suivant les directions parallèles à l'axe, , p. 731-751
- Fresnel O.C. Vol.1, 1866, Mémoire sur la loi des modifications imprimée à la lumière polarisée par sa réflexion totale dans l'intérieur des corps transparents, , p. 767-799
- Lewitt 2013, p. 57.
- Lewitt 2013, p. 71.
- Eugène Péclet, Traité élémentaire de physique (Vomlume 2), Paris, Hachette, (lire en ligne), p. 254
- Arago 1830, p. 475.
- Louis Le Cunff, Feux de mer, Saint-Malo, L'Ancre de Marine, , 248 p. (ISBN 2-905970-44-8, lire en ligne), p. 70-75
- Péclet 1838.
- Levitt 2013, p. 59-66.
- Levitt 2013, p. 71.
- Fresnel 1822, p. 13-25.
- Philippe Monot, « Wagner Bernard Henri », sur horloge-edifice.fr, (consulté le )
- Levitt 2013, p. 72-73.
- Arago 1830, p. 476.
- Levitt 2013, p. 82.
- Arago 1830, p. 470.
- Levitt 2013, p. 84.
- (en) J. Elton, « A light to lighten the darkness: Lighthouse optics and the later development of Fresne's revolutionnary refracting lens (1780-1900) », International Journal for the History of Engeneering & Technology Vol.79 n°2, , p. 183-244
- Levitt 2013, p. 82-84.
- Levitt 2013, p. 79-80.
- Le Cunff 1992, p. 74.
- Le Cunff 1992, p. 75.
- Sur cette adaptation des lentilles au cinéma, voir le documentaire Louis Cochet. D'une lumière l'autre (Spleen Productions, 2011), réalisé par Michel Caron et Jean-Pierre Gestin
- « Augustin Jean Fresnel (1788-1827) », sur utc.fr
- Silliman 1967, p. 276–277.
- Boutry 1948, p. 601–602.
- Silliman 1967, p. 278.
- Fresnel O.C. 1868, p. 667–672.
- Fresnel O.C. 1868, p. 647–660.
- Boutry 1948, p. 603.
- Arago 1830, p. 484.
- Jules Moiroux, Le cimetière du Père Lachaise, Paris, S. Mercadier, (lire en ligne), p. 164
- Arago 1830, p. 477.
- Emile Picard, Anton Lorentz, Charles Fabry, Discours prononcés lors de la cérémonie du centenaire de la mort d'Augustin Fresnel, Paris, Académie des Sciences, , 33 p. (lire en ligne)
Voir aussi
[modifier | modifier le code]Bibliographie
[modifier | modifier le code]- François Arago, Fresnel. Biographie lue en séance publique de l'Académie des sciences le 26 juillet 1830, Paris, Mémoires de l'Académie des sciences, (lire en ligne), p. 410
- Jean-Louis Basdevant, « Le mémoire de Fresnel sur la diffraction de la lumière », sur bibnum.education.fr, (consulté le )
- Nicole Bensacq-Tixier, Dictionnaire biographique du Corps impérial des ingénieurs des ponts et chaussées (mémoire de maîtrise d'histoire), Paris, Université Paris-Sorbonne - Paris IV, , 186 p., p. 68-69.
- Luc Chanteloup et Vincent Guigueno, « La lentille à échelons : œil des phares, gloire des Fresnel », Les Génies de la science, no 24, , p. 20-23.
- Alfred Cornu, « Fresnel (1788-1827) », Livre du Centenaire de l'École Polytechnique, Société des amis de la bibliothèque et de l'histoire de l'École polytechnique, (lire en ligne, consulté le ).
- (en) Olivier Darrigol, 2012,, Oxford, ., A History of Optics: From Greek Antiquity to the Nineteenth Century, Oxford, (ISBN 978-0-19-964437-7), p. 198-199
- Léonor Fresnel, « Mémoire sur la stabilité du phare en construction à Belle-Île (océan) », Annales des ponts et chaussées, 1re série, vol. 2, , p. 385-420 (lire en ligne).
- Suzanne Gély, « André Marie Ampère (1775-1836) et Augustin Fresnel (1788-1827) », Bulletin de la Sabix, Société des amis de la bibliothèque et de l'histoire de l'École polytechnique, no 37, , p. 52-55 (lire en ligne [PDF], consulté le ).
- Vincent Guigueno, Au service des phares (thèse de doctorat d'histoire), Paris, Université Panthéon-Sorbonne - Paris I, , 396 p..
- Frédéric Leclercq, « Arago, Biot et Fresnel expliquent la polarisation rotatoire », Revue d'histoire des sciences, vol. 66, no 2, , p. 395-416.
- (en) T.H. Levitt, A Short Bright Flash: Augustin Fresnel and the Birth of the Modern Lighthouse, New York, W.W. Norton, (ISBN 978-0-393-35089-0)
- Gérard Mourou, Michel Menu et Monica Preti, L'impressionnisme entre art et science - La lumière au prisme d'Augustin Fresnel (de 1790 à 1900), Paris, Hermann, , 209 p. (ISBN 978 2 7056 9462 3).
- (en) R.H. Silliman, Augustin Fresnel (1788–1827) and the Establishment of the Wave Theory of Light (PhD dissertation), Princeton University, Princeton University, , 352 p., p. 163-164
- Pierre Speziall, « Augustin Fresnel et les savants genevois », Revue d'histoire des sciences, vol. 10, no 3, , p. 255-259 (lire en ligne [PDF], consulté le ).
- Émile Verdet, « Introduction aux œuvres d'Augustin Fresnel », Henri de Sénarmont, Émile Verdet,et Léonor Fresnel, Œuvres complètes d'Augustin Fresnel, vol. 1, , p. IX-XCIX (lire en ligne, consulté le ).
Articles connexes
[modifier | modifier le code]- Principe de Huygens-Fresnel
- Représentation de Fresnel
- Spirale de Fresnel
- Diffraction de Fresnel
- Coefficients de Fresnel
- Lentille de Fresnel
- Entraînement partiel de l'éther
Liens externes
[modifier | modifier le code]- Académie des sciences : Augustin Fresnel
- Augustin Fresnel, père des phares modernes
- « Fresnel, Augustin (1788-1827) », sur heritage.ecoledesponts.fr
- Augustin Fresnel : sa vie et son œuvre
- Le texte de 1822 de Fresnel sur la lentille à échelons commenté sur le site BibNum.
- La biréfringence circulaire, texte de Fresnel (1822) commenté sur le site BibNum.
- Premier mémoire sur la diffraction (1815), en ligne et commenté sur le site BibNum.
- Institut Fresnel - Unité Mixte de Recherche CNRS 7249
- Structurae : Augustin Fresnel
Bases de données et dictionnaires
[modifier | modifier le code]
- Ressources relatives aux beaux-arts :
- Ressource relative à la santé :
- Ressource relative à la recherche :
- Notices dans des dictionnaires ou encyclopédies généralistes :

















































