Caustique



Une caustique désigne en optique et en mathématiques l'enveloppe des rayons lumineux subissant une réflexion ou une réfraction sur une surface ou une courbe.
Plus spécifiquement, on parle de caustique « au flambeau » lorsque les rayons lumineux sont issus d'un point à distance finie et de caustique « au soleil » si la source lumineuse se trouve à une distance infinie.
Une caustique par réflexion est aussi appelée « catacaustique », tandis qu'une caustique par réfraction est appelée « diacaustique ».
En astronomie, des caustiques sont associées aux mirages gravitationnels[1].
Étymologie et histoire
[modifier | modifier le code]
Le physicien allemand Ehrenfried Walther von Tschirnhaus consacra sa vie à l'optique géométrique et à la fabrication de lentilles et miroirs à l'usage de l'astronomie. C'est dans ce cadre qu'il étudia en 1682 les caustiques par réflexion. Il choisit le terme « caustique » en référence au mot grec kaustikos provenant de kaiein (brûler)[2].
Il prouva en outre que les caustiques des courbes algébriques sont rectifiables : on peut calculer analytiquement leur longueur, sur un intervalle donné, par le calcul intégral.
Le concept de caustique fut également étudié par Jacques Bernoulli, le Marquis de l'Hôpital et La Hire.
Anticaustique ou caustique secondaire
[modifier | modifier le code]Pour construire une caustique, il peut être utile de se servir d'une courbe auxiliaire appelée anticaustique ou caustique secondaire. C'est la développante de la caustique. Autrement dit, la caustique est la développée de sa caustique secondaire, c'est-à-dire le lieu des centres de courbure de la caustique secondaire.
Dans le cas de la caustique par réflexion d'une courbe pour une source S, la caustique secondaire est l'orthotomique de la courbe par rapport à S, c'est-à-dire le lieu des symétriques de S par rapport aux tangentes à la courbe [3],[4].
Dans le cas de la caustique par réfraction d'indice n d'une courbe pour une source S, la caustique secondaire est l'enveloppe des cercles[5] de centres M appartenant à la courbe et de rayons .
Exemples géométriques
[modifier | modifier le code]Caustiques de cercles
[modifier | modifier le code]La courbe réfléchissante est ici un cercle. Lorsque la source lumineuse est un point infiniment éloigné, la caustique est une néphroïde. Lorsque la source est sur le bord du cercle, c'est une cardioïde.
Ci-dessous, une animation décrit l'évolution d'une caustique de cercle lorsque la source lumineuse (représentée par un point bleu) parcourt une droite passant par le centre du cercle. On observe en particulier le passage d'une néphroïde à une cardioïde. Seuls le cercle réfléchissant et la caustique sont représentés, sans les rayons incidents et réfléchis. La caustique et la source peuvent être réels, ou virtuels (i.e. situés sur les prolongements des rayons au-delà du cercle réfléchissant)[6].

Caustique de cycloïde
[modifier | modifier le code]La surface réfléchissante est une cycloïde, la source lumineuse étant infiniment loin dans l'axe de la cycloïde. La caustique est constituée de deux cycloïdes deux fois plus petites que la cycloïde initiale.

Caustiques de parabole
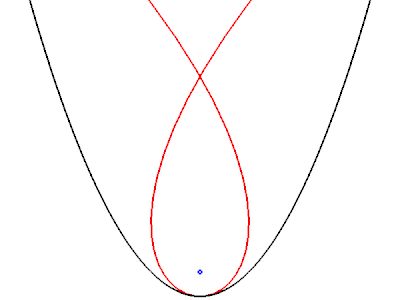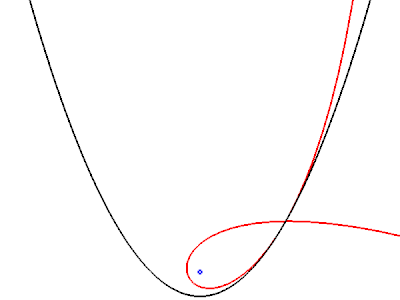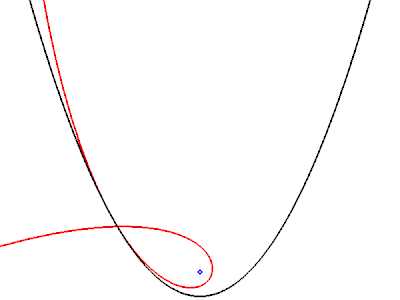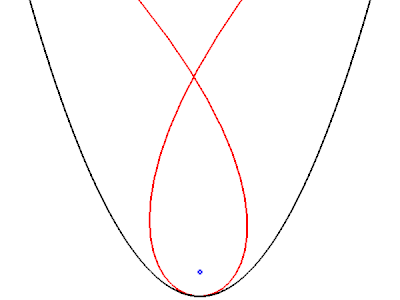
[modifier | modifier le code]Lorsque la surface réfléchissante est une parabole et que la source lumineuse est à l'infini, la caustique est une cubique de Tschirnhausen. Lorsque la direction de la source varie, toutes les caustiques engendrées restent semblables entre elles, par une similitude de centre le foyer de la parabole. La cubique se réduit à ce foyer lorsque la direction de la source est l'axe de la parabole[7].
Ci-dessous à gauche, on représente une telle caustique. Seuls les rayons réfléchis sont représentés. La direction des rayons incidents (non représentés) est donnée par celle de la tangente commune à la parabole et à la caustique, en noir. Les rayons réfléchis sur la gauche de la parabole proviennent d'une source à l'infini vers la droite, ceux réfléchis sur la droite de la parabole proviennent d'une source à l'infini vers la gauche. Dans la figure de droite, on montre comment varie la caustique lorsque la direction de la source tourne dans le sens trigonométrique : on représente seulement la parabole et la caustique, mais ni les rayons incidents, ni les rayons réfléchis.
Caustiques de deltoïde
[modifier | modifier le code]Lorsque la surface réfléchissante est un deltoïde et que la source lumineuse est à l'infini, la caustique est une astroïde. Lorsque la direction de la source varie, toutes les caustiques engendrées restent isométriques entre elles[7]. Ci-dessous, à gauche, on a représenté le deltoïde et sa caustique. A droite, l'animation montre l'évolution de la caustique lorsque la direction de la source varie. La courbe bleue est une courbe auxiliaire, lieu des points de rebroussement de la caustique. Il s'agit d'une épicycloïde à trois rebroussements.
|
Caustique et roulement sans glissement
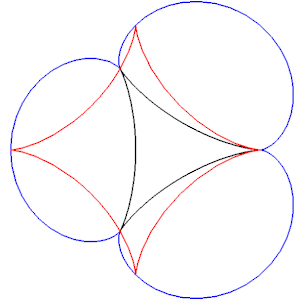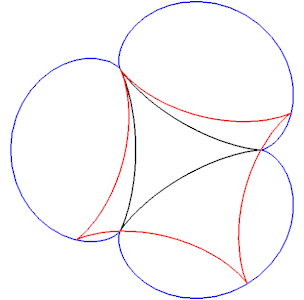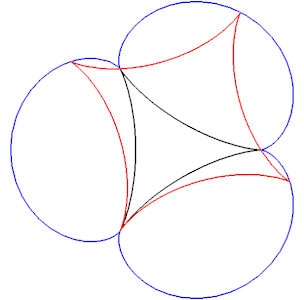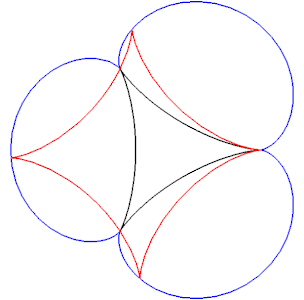
[modifier | modifier le code]On a vu plus haut que la cardioïde et la néphroïde étaient des caustiques de cercles. Or ces deux courbes sont connues pour être engendrées par le point d'un cercle roulant sans glisser sur un autre cercle. Cette situation n'est qu'un cas particulier, à rayon constant, d'un résultat plus général. Le théorème de Boyle[7] énonce que, pour toute caustique par réflexion, il existe une courbe auxiliaire et un cercle de rayon variable roulant sans glisser sur la courbe auxiliaire tout en restant tangent à la courbe réfléchissante, et dont l'un des points décrit la caustique. On illustre cette propriété par deux exemples. A gauche, on considère une caustique de cercle, intermédiaire entre la cardioïde et la néphroïde. A droite, on considère une caustique de deltoïde. Dans les deux cas, la courbe réfléchissante est en noir, la caustique en rouge, la courbe auxilaire en bleu.
Notes et références
[modifier | modifier le code]- « Simulateur de mirages gravitationnels », sur ulg.ac.be.
- Sous la direction d'Alain Rey, Dictionnaire historique de la langue française, Le Robert, (ISBN 2-85036-187-9)
- Robert Ferreol et Jacques Mandonnet, « Caustique », sur Encyclopédie des formes mathématiques remarquables (mathcurve), .
- (en) J. W. Bruce, P. J. Giblin, C. G. Gibson, « On caustics of plane curves », Amer. Math. Monthly, no 88, , p. 651-667
- Robert Ferreol et Jacques Mandonnet, « Anticaustique », sur Encyclopédie des formes mathématiques remarquables (mathcurve), .
- (en) Arthur Cayley, « A memoir upon caustics », Philos. Trans. R. Soc. London, no 147, , p. 295-296 (lire en ligne)
- (en) Jeffrey A. Boyle, « Using rolling circles to generate caustic envelopes resulting from reflected light », Amer. Math. Monthly, vol. 122, no 5, , p. 452-466 (lire en ligne)
Voir aussi
[modifier | modifier le code]Article connexe
[modifier | modifier le code]- L'Analyse des infiniment petits pour l'intelligence des lignes courbes, du marquis de l'Hôpital consacre deux chapitres à l'étude des caustiques.
- Point de rebroussement
Lien externe
[modifier | modifier le code]Michèle Audin, « Des caustiques dans la vie quotidienne », sur Images des mathématiques
Bibliographie
[modifier | modifier le code]- A. Bouvier, M. George, F. Le Lionnais, Dictionnaire des mathématiques, PUF (1979)
- (en) Jeffrey A. Boyle, « Using rolling circles to generate caustic envelopes resulting from reflected light », Amer. Math. Monthly, vol. 122, no 5, , p. 452-466 (lire en ligne)
- (en) Arthur Cayley, « A memoir upon caustics », Philos. Trans. R. Soc. London, no 147, , p. 273-312 (lire en ligne)