Décagone

| Décagone régulier | |
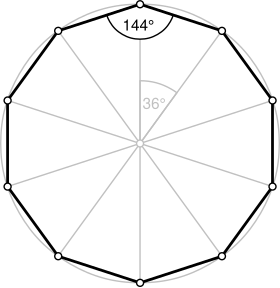 | |
| Type | Polygone régulier |
|---|---|
| Arêtes | 10 |
| Sommets | 10 |
| Symbole de Schläfli | {10} |
| Angle interne | 144° |
| Propriétés | Constructible |
| modifier | |
Un décagone est un polygone à 10 sommets, donc 10 côtés et 35 diagonales.
La somme des angles internes d'un décagone non croisé vaut 1 440°.
Un décagone régulier est un décagone dont les dix côtés ont la même longueur et dont les angles internes ont même mesure. Il y en a deux : un étoilé (le décagramme noté {10/3}) et un convexe (noté {10}). C'est de ce dernier qu'il s'agit lorsqu'on dit « le décagone régulier ». Il est constructible.
Aire d'un décagone régulier
[modifier | modifier le code]L'aire d'un décagone régulier de côté a vaut
Constructions d'un décagone régulier
[modifier | modifier le code]Construction approximative à l'aide du rapporteur
[modifier | modifier le code]Cette construction est excessivement simple mais n'est pas forcément exacte :
- Tracer un cercle Γ de centre O.
- Soit A un point quelconque appartenant à Γ.
- Il suffit alors de placer le point B sur Γ de façon que l'angle mesure 36°. En effet, on a 360/10 = 36°. Pour placer le point B, il faut utiliser un rapporteur, ce qui peut être source d'inexactitudes dans le reste de la construction (un rapporteur n'est jamais très précis).
- Il ne reste plus qu'à reporter AB sur le cercle de manière à obtenir les 8 sommets restants.
- Enfin on relie les différents sommets entre eux de manière à obtenir un décagone (à peu près) régulier.
Construction exacte à partir d'un pentagone
[modifier | modifier le code]Après avoir construit un pentagone régulier, il est facile de construire un décagone régulier : par bissection.
- Tracer un cercle qui passe par tous les sommets du pentagone.
- Tracer le milieu de chaque côté du pentagone.
- Tracer un segment qui joint le centre du pentagone au point milieu de chaque côté et qui touche le cercle.
- Joindre, avec des segments, toutes les paires de points voisins qui touchent au cercle.
Construction exacte à partir d'un rectangle d'or
[modifier | modifier le code]
- Tracer un cercle Γ de centre O et de diamètre [AB].
- La médiatrice de [AB] (passant donc par O et perpendiculaire à [AB]) coupe le cercle Γ en deux points. Soit D l'un de ces points.
- Tracer le milieu C de [OA].
- Le cercle de centre C et de rayon CD coupe [OB] en E (les proportions AE/OA et OA/OE sont égales au nombre d'or).
- Reporter 10 fois de suite la longueur OE sur le cercle Γ (à partir d'un point quelconque du cercle) pour obtenir les sommets d'un décagone régulier.
- Relier les différents sommets de manière à obtenir un décagone régulier.
Variante de la construction précédente
[modifier | modifier le code]
- Tracer Γ, O, A, B, C, D, E comme ci-dessus.
- Le cercle de centre C et de rayon OC coupe [CD] en F.
- Terminer comme ci-dessus en reportant 10 fois la longueur DF (égale à la longueur OE précédente).
Voir aussi
[modifier | modifier le code]Articles connexes
[modifier | modifier le code]- Théorème de Gauss-Wantzel
- Table de lignes trigonométriques exactes
- Nombre décagonal
- Nombre décagonal centré

