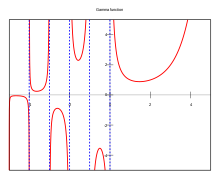
Tracé de la fonction gamma le long de l'axe des réels. En mathématiques , la fonction gamma (notée par Γ la lettre grecque majuscule gamma de l'alphabet grec ) est une fonction utilisée communément, qui prolonge la fonction factorielle à l'ensemble des nombres complexes . En ce sens, il s'agit d'une fonction complexe . Elle est considérée également comme une fonction spéciale [pourquoi ?] entiers négatifs. On a pour tout entier n {\displaystyle n}
Γ ( n ) = ( n − 1 ) ! {\displaystyle \Gamma (n)=(n-1)!}
où ( n − 1 ) ! {\displaystyle (n-1)!} n − 1 {\displaystyle n-1} n − 1 {\displaystyle n-1} ( n − 1 ) ! = 1 × 2 × ⋯ × ( n − 1 ) {\displaystyle (n-1)!=1\times 2\times \dots \times (n-1)}
Tracé du module de la fonction gamma dans le plan complexe. On définit la fonction gamma , et notée par la lettre grecque Γ (gamma majuscule) de la façon suivante. Pour tout z {\displaystyle z}
Γ ( z ) = ∫ 0 + ∞ t z − 1 e − t d t {\displaystyle \Gamma (z)=\int _{0}^{+\infty }t^{z-1}\,\mathrm {e} ^{-t}\,\mathrm {d} t} C'est une intégrale paramétrée par z {\displaystyle z} t {\displaystyle t} intégrale impropre converge absolument sur le demi-plan complexe où la partie réelle est strictement positive[ 1] intégration par parties [ 1]
Γ ( z + 1 ) = z Γ ( z ) {\displaystyle \Gamma (z+1)=z\;\Gamma (z)} Cette fonction peut être prolongée analytiquement en une fonction méromorphe sur l'ensemble des nombres complexes, excepté pour z = 0, −1, −2, −3… qui sont des pôles . C'est ce prolongement qu'on appelle généralement « fonction gamma ». L'unicité du prolongement analytique permet de montrer que la fonction prolongée vérifie encore l'équation fonctionnelle précédente. Cela permet une définition plus simple, à partir de l'intégrale, et un calcul de proche en proche de Γ pour z – 1, z – 2, etc.
Par changement de variable , l'intégrale précédente (pour Re(z ) > 0 ) s'écrit aussi :
Γ ( z ) = 2 ∫ 0 + ∞ u 2 z − 1 e − u 2 d u et Γ ( z ) = ∫ 0 1 ( − ln s ) z − 1 d s {\displaystyle \Gamma (z)=2\int _{0}^{+\infty }u^{2z-1}\mathrm {e} ^{-u^{2}}\,\mathrm {d} u\quad {\text{et}}\quad \Gamma (z)=\int _{0}^{1}\left(-\ln s\right)^{z-1}\,\mathrm {d} s} La définition suivante de la fonction gamma par produits infinis , due à Euler , a un sens pour les nombres complexes z qui ne sont pas des entiers négatifs ou nuls[ 2]
Γ ( z ) = lim n → + ∞ n ! n z z ( z + 1 ) ⋯ ( z + n ) = 1 z ∏ k = 1 + ∞ ( 1 + 1 k ) z 1 + z k {\displaystyle \Gamma (z)=\lim _{n\to {+\infty }}{\frac {n!\;n^{z}}{z\;(z+1)\cdots (z+n)}}={\frac {1}{z}}\,\prod _{k=1}^{+\infty }{\frac {\left(1+{\frac {1}{k}}\right)^{z}}{1+{\frac {z}{k}}}}} Elle est équivalente à celle donnée par Schlömilch [ 3] , [ 4] , [ 5]
Γ ( z ) = e − γ z z ∏ k = 1 + ∞ e z k 1 + z k {\displaystyle \Gamma (z)={\frac {\operatorname {e} ^{-\gamma z}}{z}}\prod _{k=1}^{+\infty }{\frac {\operatorname {e} ^{\frac {z}{k}}}{1+{\frac {z}{k}}}}} où γ = ∑ k = 1 ∞ [ 1 k − ln ( 1 + 1 k ) ] {\displaystyle \gamma =\sum _{k=1}^{\infty }\left[{\frac {1}{k}}-\ln \left(1+{\frac {1}{k}}\right)\right]} constante d'Euler-Mascheroni .
De Γ(z +1) = z Γ (z ) et Γ(1) = 1
∀ n ∈ N , Γ ( n + 1 ) = n ! {\displaystyle \forall \,n\in \mathbb {N} ,\;\Gamma (n+1)=n!} On interprète donc la fonction gamma comme un prolongement de la factorielle à l'ensemble des nombres complexes (à l'exception des entiers négatifs ou nuls).
Une notation alternative est la fonction Π , introduite par Gauss :
Π ( z ) = Γ ( z + 1 ) = z Γ ( z ) {\displaystyle \Pi (z)=\Gamma (z+1)=z\;\Gamma (z)} Γ ( z ) = Π ( z − 1 ) = Π ( z ) / z {\displaystyle \Gamma (z)=\Pi (z-1)=\Pi (z)/z} de telle façon que :
Π ( n ) = n ! {\displaystyle \Pi (n)=n!} La fonction gamma est entièrement caractérisée sur R + ∗ {\displaystyle \mathbb {R} _{+}^{*}} théorème de Bohr-Mollerup ) :
Γ ( 1 ) = 1 {\displaystyle \Gamma (1)=1\,} Pour tout x > 0 {\displaystyle x>0\,} Γ ( x + 1 ) = x Γ ( x ) {\displaystyle \Gamma (x+1)=x\;\Gamma (x)\,} la fonction composée ln ∘ Γ {\displaystyle \ln \circ \,\Gamma } R + ∗ {\displaystyle \mathbb {R} _{+}^{*}} La fonction gamma est entièrement caractérisée parmi les fonctions holomorphes du demi-plan complexe Re(z )>0 par les trois propriétés suivantes (théorème de Wielandt ) :
Γ ( 1 ) = 1 {\displaystyle \Gamma (1)=1\,} Pour tout z tel que Re(z ) > 0 , Γ ( z + 1 ) = z Γ ( z ) {\displaystyle \Gamma (z+1)=z\;\Gamma (z)\,} | Γ ( z ) | {\displaystyle |\Gamma (z)|\,} z ) ≤ 2.La fonction gamma vérifie la formule de réflexion d'Euler, ou formule des compléments
∀ z ∈ C ∖ Z Γ ( 1 − z ) Γ ( z ) = π sin ( π z ) , {\displaystyle \forall z\in \mathbb {C} \setminus \mathbb {Z} \quad \Gamma (1-z)\;\Gamma (z)={\pi \over \sin(\pi z)},} que l'on démontre en remarquant d'abord que Γ(1 – z )Γ(z ) est 2-périodique et a les mêmes pôles et résidus que π sin ( π z ) {\displaystyle {\tfrac {\pi }{\sin(\pi z)}}}
La fonction gamma vérifie également la formule de duplication : Γ ( z ) Γ ( z + 1 2 ) = 2 1 − 2 z π Γ ( 2 z ) . {\displaystyle \Gamma (z)\;\Gamma \left(z+{\frac {1}{2}}\right)=2^{1-2z}\;{\sqrt {\pi }}\;\Gamma (2z).}
La formule de duplication est un cas particulier du théorème de multiplication :
Γ ( z ) Γ ( z + 1 m ) Γ ( z + 2 m ) ⋯ Γ ( z + m − 1 m ) = ( 2 π ) ( m − 1 ) / 2 m 1 / 2 − m z Γ ( m z ) . {\displaystyle \Gamma (z)\;\Gamma \left(z+{\frac {1}{m}}\right)\;\Gamma \left(z+{\frac {2}{m}}\right)\cdots \Gamma \left(z+{\frac {m-1}{m}}\right)=(2\pi )^{(m-1)/2}\;m^{1/2-mz}\;\Gamma (mz).} Cette fonction apparaît également dans des formules incluant la fonction zêta de Riemann .
La fonction gamma possède un pôle d'ordre 1 en z = −n pour tout entier naturel n . Le résidu de la fonction en ce pôle est donné par :
Res ( Γ , − n ) = ( − 1 ) n n ! . {\displaystyle \operatorname {Res} (\Gamma ,-n)={\frac {(-1)^{n}}{n!}}.} La fonction gamma est infiniment dérivable sur R + ∗ {\displaystyle \mathbb {R} _{+}^{*}} p fois dérivable pour tout entier p ). Sa dérivée est exprimée à l'aide de la fonction digamma : Γ ′ ( z ) = Γ ( z ) ψ 0 ( z ) . {\displaystyle \Gamma '(z)=\Gamma (z)\psi _{0}(z).\,}
Plus généralement, sa dérivée p -ième possède sur R + ∗ {\displaystyle \mathbb {R} _{+}^{*}}
Γ ( p ) ( x ) = ∫ 0 + ∞ ( ln t ) p t x − 1 e − t d t {\displaystyle \Gamma ^{(p)}(x)=\int _{0}^{+\infty }{(\ln t)^{p}\,t^{x-1}\,\operatorname {e} ^{-t}\,\mathrm {d} t}} La définition de la fonction gamma sous forme d'intégrale la fait apparaître comme une convolution entre un caractère additif (l'exponentielle) et un caractère multiplicatif ( x ↦ x s {\displaystyle x\mapsto x^{s}}
La fonction gamma est reliée à la fonction ζ de Riemann par :
ζ ( s ) Γ ( s ) = ∫ 0 + ∞ t s − 1 e t − 1 d t {\displaystyle \zeta (s)\,\Gamma (s)=\int _{0}^{+\infty }{\frac {t^{s-1}}{\mathrm {e} ^{t}-1}}\,\mathrm {d} t} Elle est reliée à la fonction êta de Dirichlet par[ 6]
Γ ( s ) η ( s ) = ∫ 0 ∞ x s − 1 e x + 1 d x = ∫ 0 1 ∫ 0 1 ( − ln ( x y ) ) s − 2 1 + x y d x d y {\displaystyle \Gamma (s)\,\eta (s)=\int _{0}^{\infty }{\frac {x^{s-1}}{\mathrm {e} ^{x}+1}}\,\mathrm {d} x=\int _{0}^{1}\int _{0}^{1}{\frac {(-\ln(xy))^{s-2}}{1+xy}}\,\mathrm {d} x\,\mathrm {d} y} Dans la définition de la fonction gamma sous forme d'intégrale, les bornes de l'intégrale sont fixées ; la fonction gamma incomplète est la fonction obtenue en modifiant la borne inférieure ou la borne supérieure.
La fonction gamma est reliée à la fonction bêta par la formule :
B ( x , y ) = Γ ( x ) Γ ( y ) Γ ( x + y ) . {\displaystyle \mathrm {B} (x,y)={\frac {\Gamma (x)\;\Gamma (y)}{\Gamma (x+y)}}.} Le logarithme de la fonction gamma est parfois appelé lngamma . Il intervient notamment dans la résolution des problèmes de propagation d’ondes [ 7] équation fonctionnelle de la fonction lngamma est :
ln Γ ( z ) = ln Γ ( z + 1 ) − ln ( z ) {\displaystyle \ln \Gamma (z)=\ln \Gamma (z+1)-\ln(z)} Si l’on connaît les valeurs de la fonction sur une bande de largeur 1 en Re(z ), on obtient par cette relation les valeurs dans une bande voisine de même largeur, et l’on peut répéter ce procédé. Partant d’un z avec Re(z ) >> 1 pour lequel on connaît une bonne approximation, on peut ainsi atteindre la valeur pour un z quelconque.
Rocktaeschel (1922[ 8] Re(z ) grand :
ln Γ ( z ) ≈ ( z − 1 2 ) ln z − z + 1 2 ln ( 2 π ) {\displaystyle \ln \Gamma (z)\approx (z-{\tfrac {1}{2}})\ln z-z+{\tfrac {1}{2}}\ln(2\pi )} On peut en déduire une approximation de ln Γ(z ) pour Re(z ) plus petit, en utilisant[ 9]
ln Γ ( z − m ) = ln Γ ( z ) − ∑ k = 1 m ln ( z − k ) {\displaystyle \ln \Gamma (z-m)=\ln \Gamma (z)-\sum _{k=1}^{m}\ln(z-k)} La dérivée logarithmique de la fonction gamma est appelée fonction digamma . Les dérivées d'ordre supérieur sont les fonctions polygamma .
Un analogue de la fonction gamma sur un corps fini ou un anneau fini est fourni par les sommes de Gauss .
D'après l'expression d'Euler pour la fonction gamma (voir supra son inverse (en) g ( z ) = 1 Γ ( z ) {\displaystyle g(z)={\frac {1}{\Gamma (z)}}} fonction entière .
Cette section indique quelques valeurs particulières de la fonction gamma (en)
La valeur de Γ(1/2) = √π est celle de l'intégrale de Gauss ; elle peut aussi se déduire de la formule des compléments . Cette valeur permet, par récurrence , de déterminer les autres valeurs de la fonction gamma pour les demi-entiers positifs :
Γ ( 3 / 2 ) = π 2 , Γ ( 5 / 2 ) = 3 π 4 , … , {\displaystyle \Gamma (3/2)={\frac {\sqrt {\pi }}{2}},\quad \Gamma (5/2)={\frac {3{\sqrt {\pi }}}{4}},\ldots ,} Γ ( n + 1 2 ) = ( n − 1 2 ) Γ ( n − 1 2 ) = ( n − 1 2 ) ( n − 3 2 ) ⋯ 3 2 1 2 Γ ( 1 2 ) = ( 2 n ) ! 2 2 n n ! π {\displaystyle \Gamma \left(n+{\frac {1}{2}}\right)=\left(n-{\frac {1}{2}}\right)\Gamma \left(n-{\frac {1}{2}}\right)=\left(n-{\frac {1}{2}}\right)\left(n-{\frac {3}{2}}\right)\cdots {\frac {3}{2}}\,{\frac {1}{2}}\,\Gamma \left({\frac {1}{2}}\right)={\frac {(2n)!}{2^{2n}n!}}{\sqrt {\pi }}} mais aussi négatifs, par exemple :
Γ ( − 1 / 2 ) = − 2 π {\displaystyle \Gamma (-1/2)=-2{\sqrt {\pi }}} En ce qui concerne ses dérivées, avec γ la constante d'Euler-Mascheroni :
Γ ′ ( n + 1 ) = Γ ( n + 1 ) ψ 0 ( n + 1 ) = n ! ( − γ + ∑ 1 ≤ k ≤ n 1 k ) {\displaystyle \Gamma '(n+1)=\Gamma (n+1)\psi _{0}(n+1)=n!\left(-\gamma +\sum _{1\leq k\leq n}{\frac {1}{k}}\right)} Γ ′ ( n + 1 2 ) = Γ ( n + 1 2 ) ψ 0 ( n + 1 2 ) = ( 2 n ) ! 2 2 n n ! π ( − γ − 2 ln 2 + ∑ 1 ≤ k ≤ n 2 2 k − 1 ) {\displaystyle \Gamma '\left(n+{\frac {1}{2}}\right)=\Gamma \left(n+{\frac {1}{2}}\right)\psi _{0}\left(n+{\frac {1}{2}}\right)={\frac {(2n)!}{2^{2n}n!}}{\sqrt {\pi }}\left(-\gamma -2\ln 2+\sum _{1\leq k\leq n}{\frac {2}{2k-1}}\right)} Γ ″ ( 1 / 2 ) = π ( γ + 2 ln ( 2 ) ) 2 + π 5 / 2 2 , Γ ″ ( 1 ) = γ 2 + π 2 6 , Γ ″ ( 2 ) = ( 1 − γ ) 2 + π 2 6 − 1 {\displaystyle \Gamma ''(1/2)={\sqrt {\pi }}(\gamma +2\,\ln(2))^{2}+{\frac {\pi ^{5/2}}{2}},\quad \Gamma ''(1)=\gamma ^{2}+{\frac {\pi ^{2}}{6}},\quad \Gamma ''(2)=(1-\gamma )^{2}+{\frac {\pi ^{2}}{6}}-1} On connaît quelques résultats de transcendance et même d'indépendance algébrique sur les valeurs de Γ en certains points rationnels .
Une conjecture de Rohrlich [ 10]
π b / 2 ∏ Γ ( a k ) m k ∈ Q ¯ , ( b ∈ Z , a k ∈ Q , m k ∈ Z ) {\displaystyle \pi ^{b/2}\prod \Gamma (a_{k})^{m_{k}}\in {\overline {\mathbb {Q} }},\quad (b\in \mathbb {Z} ,\;a_{k}\in \mathbb {Q} ,\;m_{k}\in \mathbb {Z} )} (où ℚ désigne le corps des nombres algébriques ) se déduit des trois relations standard :
Γ ( z + 1 ) = z Γ ( z ) , Γ ( 1 − z ) Γ ( z ) = π sin ( π z ) , ∏ 0 ≤ k < n Γ ( z + k n ) = ( 2 π ) ( n − 1 ) / 2 n − n z + 1 / 2 Γ ( n z ) {\displaystyle \Gamma (z+1)=z\Gamma (z),\quad \Gamma (1-z)\Gamma (z)={\pi \over \sin(\pi z)},\quad \prod _{0\leq k<n}\Gamma \left(z+{\frac {k}{n}}\right)=(2\pi )^{(n-1)/2}n^{-nz+1/2}\Gamma (nz)} La formule de Stirling donne un équivalent au voisinage de l'infini de la factorielle :
n ! = 2 π n n + 1 2 e − n + μ ( n ) pour n ∈ N , {\displaystyle n\,!={\sqrt {2\pi }}\,n^{n+{\frac {1}{2}}}{\rm {e}}^{-n+\mu (n)}{\text{ pour }}n\in \mathbb {N} \ ,} avec μ la fonction de Binet :
μ ( z ) = ∑ k = 1 ∞ B 2 k 2 k ( 2 k − 1 ) z 2 k − 1 , {\displaystyle \mu (z)=\sum _{k=1}^{\infty }{\frac {B_{2k}}{2k(2k-1)z^{2k-1}}}\ ,} et Bi les nombres de Bernoulli . Sachant que Γ(n +1)=n ! sur ℕ , cet équivalent se généralise à la fonction gamma :
Γ ( z + 1 ) = 2 π z z + 1 2 e − z + μ ( z ) pour z ∈ C ∖ Z − ∗ , {\displaystyle \Gamma (z+1)={\sqrt {2\pi }}\,z^{z+{\frac {1}{2}}}{\rm {e}}^{-z+\mu (z)}{\text{ pour }}z\in \mathbb {C} \setminus \mathbb {Z_{-}^{*}} \ ,} d’où :
Γ ( z ) = Γ ( z + 1 ) z = 2 π z z − 1 2 e − z + μ ( z ) pour z ∈ C ∖ Z − . {\displaystyle \Gamma (z)={\frac {\Gamma (z+1)}{z}}={\sqrt {2\pi }}\,z^{z-{\frac {1}{2}}}{\rm {e}}^{-z+\mu (z)}{\text{ pour }}z\in \mathbb {C} \setminus \mathbb {Z_{-}} \ .} En calculant les premiers termes de e μ grâce à la formule exponentielle , on obtient le développement asymptotique :
Γ ( z ) = 2 π z z − 1 2 e − z [ 1 + 1 12 z + 1 288 z 2 − 139 51840 z 3 − 571 2488320 z 4 + 163879 209018880 z 5 + O ( 1 z 6 ) ] . {\displaystyle \Gamma (z)={\sqrt {2\pi }}\,z^{z-{\frac {1}{2}}}{\rm {e}}^{-z}\left[1+{\frac {1}{12z}}+{\frac {1}{288z^{2}}}-{\frac {139}{51840z^{3}}}-{\frac {571}{2488320z^{4}}}+{\frac {163879}{209018880z^{5}}}+{\mathcal {O}}\left({\frac {1}{z^{6}}}\right)\right]\ .} L’équivalent en z +½
Γ ( z + 1 2 ) = 2 π z z e − z + β ( z ) , {\displaystyle \Gamma \left(z+{\frac {1}{2}}\right)={\sqrt {2\pi }}\,z^{z}{\rm {e}}^{-z+\beta (z)}\ ,} avec :
β ( z ) = ∑ k = 1 ∞ ( 1 2 2 k − 1 − 1 ) B 2 k 2 k ( 2 k − 1 ) z 2 k − 1 , {\displaystyle \beta (z)=\sum _{k=1}^{\infty }{\frac {\left({\frac {1}{2^{2k-1}}}-1\right)B_{2k}}{2k(2k-1)z^{2k-1}}}\ ,} d’où le développement asymptotique :
Γ ( z + 1 2 ) = 2 π z z e − z [ 1 − 1 24 z + 1 1152 z 2 + 1003 414720 z 3 − 4027 39813120 z 4 − 5128423 6688604160 z 5 + O ( 1 z 6 ) ] . {\displaystyle \Gamma \left(z+{\frac {1}{2}}\right)={\sqrt {2\pi }}\,z^{z}{\rm {e}}^{-z}\left[1-{\frac {1}{24z}}+{\frac {1}{1152z^{2}}}+{\frac {1003}{414720z^{3}}}-{\frac {4027}{39813120z^{4}}}-{\frac {5128423}{6688604160z^{5}}}+{\mathcal {O}}\left({\frac {1}{z^{6}}}\right)\right]\ .} De manière plus générale, pour |a | < |z | , l’équivalent en z + a ∉ ℤ-
Γ ( z + a ) = 2 π z z + a − 1 2 exp ( − z − ∑ k = 2 ∞ B k ( a ) k ( k − 1 ) ( − z ) k − 1 ) {\displaystyle \Gamma (z+a)={\sqrt {2\pi }}\,z^{z+a-{\frac {1}{2}}}\exp \left(-z-\sum _{k=2}^{\infty }{\frac {B_{k}(a)}{k(k-1)(-z)^{k-1}}}\right)} où B k polynômes de Bernoulli .
Démonstration
Par généralisation sur les complexes de la formule de Stirling, on sait que, pour z ∉ ℤ-
Γ ( z ) = 2 π z z − 1 2 exp ( − z + ∑ k = 1 ∞ B 2 k 2 k ( 2 k − 1 ) z 2 k − 1 ) {\displaystyle \Gamma (z)={\sqrt {2\pi }}\,z^{z-{\frac {1}{2}}}\exp \left(-z+\sum _{k=1}^{\infty }{\frac {B_{2k}}{2k(2k-1)z^{2k-1}}}\right)} Les nombres de Bernoulli de rang impair supérieur ou égal à 3 étant nuls , on peut également écrire, par changement de variable i = 2k
Γ ( z ) = 2 π z z − 1 2 exp ( − z + ∑ i = 2 ∞ B i i ( i − 1 ) z i − 1 ) {\displaystyle \Gamma (z)={\sqrt {2\pi }}\,z^{z-{\frac {1}{2}}}\exp \left(-z+\sum _{i=2}^{\infty }{\frac {B_{i}}{i(i-1)z^{i-1}}}\right)} d’où :
Γ ( z + a ) = 2 π ( z + a ) z + a − 1 2 exp ( − ( z + a ) + ∑ i = 2 ∞ B i i ( i − 1 ) ( z + a ) i − 1 ) {\displaystyle \Gamma (z+a)={\sqrt {2\pi }}\,(z+a)^{z+a-{\frac {1}{2}}}\exp \left(-(z+a)+\sum _{i=2}^{\infty }{\frac {B_{i}}{i(i-1)(z+a)^{i-1}}}\right)} z étant non nul, on peut factoriser z +a z ×(1+a /z )
Γ ( z + a ) = 2 π z z + a − 1 2 ( 1 + a z ) z + a − 1 2 exp ( − z − a + ∑ i = 2 ∞ B i i ( i − 1 ) z i − 1 ( 1 + a z ) i − 1 ) = 2 π z z + a − 1 2 exp ( − z + ( z + a − 1 2 ) ln ( 1 + a z ) − a + ∑ i = 2 ∞ B i i ( i − 1 ) z i − 1 ( 1 + a z ) − ( i − 1 ) ) . {\displaystyle {\begin{aligned}\Gamma (z+a)&={\sqrt {2\pi }}\,z^{z+a-{\frac {1}{2}}}\left(1+{\tfrac {a}{z}}\right)^{z+a-{\frac {1}{2}}}\exp \left(-z-a+\sum _{i=2}^{\infty }{\frac {B_{i}}{i(i-1)z^{i-1}(1+{\frac {a}{z}})^{i-1}}}\right)\\&={\sqrt {2\pi }}\,z^{z+a-{\frac {1}{2}}}\exp \left(-z+\left(z+a-{\frac {1}{2}}\right)\ln \left(1+{\frac {a}{z}}\right)-a+\sum _{i=2}^{\infty }{\frac {B_{i}}{i(i-1)z^{i-1}}}\left(1+{\frac {a}{z}}\right)^{-(i-1)}\right).\end{aligned}}} Ayant posé |a | < |z | , on a |a /z | < 1 , ce qui permet de développer d’une part la série de Taylor du logarithme ln(1 + x ) (valable pour |x | < 1 ) et d’autre part le binôme négatif (1 + x )-n (valable pour |x | < 1 et n ∈ ℕ*
ln ( 1 + a z ) = − ∑ k = 1 ∞ ( − a z ) k k = − ∑ k = 1 ∞ ( − a ) k k z k = − ∑ k = 2 ∞ ( − a ) k − 1 ( k − 1 ) z k − 1 {\displaystyle \ln \left(1+{\tfrac {a}{z}}\right)=-\sum _{k=1}^{\infty }{\frac {\left(-{\frac {a}{z}}\right)^{k}}{k}}=-\sum _{k=1}^{\infty }{\frac {(-a)^{k}}{k\,z^{k}}}=-\sum _{k=2}^{\infty }{\frac {(-a)^{k-1}}{(k-1)\,z^{k-1}}}} ( 1 + a z ) − ( i − 1 ) = ∑ j = 0 ∞ ( i + j − 2 j ) ( − a z ) j = ∑ j = 0 ∞ ( i + j − 2 ) ! ( − a ) j ( i − 2 ) ! j ! z j . {\displaystyle \left(1+{\tfrac {a}{z}}\right)^{-(i-1)}=\sum _{j=0}^{\infty }{\binom {i+j-2}{j}}\left(-{\frac {a}{z}}\right)^{j}=\sum _{j=0}^{\infty }{\frac {(i+j-2)!\,(-a)^{j}}{(i-2)!\,j!\,z^{j}}}.} On a donc d’une part, par le développement du logarithme :
z ln ( 1 + a z ) = − ∑ k = 1 ∞ ( − a ) k k z k − 1 = a − ∑ k = 2 ∞ ( − a ) k k z k − 1 {\displaystyle z\ln \left(1+{\tfrac {a}{z}}\right)=-\sum _{k=1}^{\infty }{\frac {(-a)^{k}}{k\,z^{k-1}}}=a-\sum _{k=2}^{\infty }{\frac {(-a)^{k}}{k\,z^{k-1}}}} et :
a ln ( 1 + a z ) = − a ∑ k = 2 ∞ ( − a ) k − 1 ( k − 1 ) z k − 1 = ∑ k = 2 ∞ ( − a ) k ( k − 1 ) z k − 1 {\displaystyle a\ln \left(1+{\tfrac {a}{z}}\right)=-a\sum _{k=2}^{\infty }{\frac {(-a)^{k-1}}{(k-1)\,z^{k-1}}}=\sum _{k=2}^{\infty }{\frac {(-a)^{k}}{(k-1)\,z^{k-1}}}} d’où :
( z + a − 1 2 ) ln ( 1 + a z ) − a = a + ∑ k = 2 ∞ ( 1 k − 1 − 1 k ) ( − a ) k z k − 1 + 1 2 ∑ k = 2 ∞ ( − a ) k − 1 ( k − 1 ) z k − 1 − a = ∑ k = 2 ∞ ( − a ) k k ( k − 1 ) z k − 1 + 1 2 ∑ k = 2 ∞ ( − a ) k − 1 ( k − 1 ) z k − 1 = ∑ k = 2 ∞ ( − a ) k + k 2 ( − a ) k − 1 k ( k − 1 ) z k − 1 . {\displaystyle {\begin{aligned}\left(z+a-{\tfrac {1}{2}}\right)\ln \left(1+{\tfrac {a}{z}}\right)-a&=a+\sum _{k=2}^{\infty }\left({\frac {1}{k-1}}-{\frac {1}{k}}\right){\frac {(-a)^{k}}{z^{k-1}}}+{\frac {1}{2}}\sum _{k=2}^{\infty }{\frac {(-a)^{k-1}}{(k-1)\,z^{k-1}}}-a\\&=\sum _{k=2}^{\infty }{\frac {(-a)^{k}}{k\,(k-1)\,z^{k-1}}}+{\frac {1}{2}}\sum _{k=2}^{\infty }{\frac {(-a)^{k-1}}{(k-1)\,z^{k-1}}}\\&=\sum _{k=2}^{\infty }{\frac {(-a)^{k}+{\frac {k}{2}}\,(-a)^{k-1}}{k\,(k-1)\,z^{k-1}}}.\end{aligned}}} On a d’autre part, par le développement du binôme négatif, puis en procédant au changement de variable k =i +j
B i i ( i − 1 ) z i − 1 ( 1 + a z ) − ( i − 1 ) = ∑ j = 0 ∞ B i ( i + j − 2 ) ! ( − a ) j i ! j ! z i − 1 + j = ∑ k = i ∞ B i ( k − 2 ) ! ( − a ) k − i i ! ( k − i ) ! z k − 1 = ∑ k = i ∞ ( k i ) B i ( − a ) k − i k ( k − 1 ) z k − 1 . {\displaystyle {\frac {B_{i}}{i\,(i-1)\,z^{i-1}}}\left(1+{\frac {a}{z}}\right)^{-(i-1)}=\sum _{j=0}^{\infty }{\frac {B_{i}\,(i+j-2)!\,(-a)^{j}}{i!\,j!\,z^{i-1+j}}}=\sum _{k=i}^{\infty }{\frac {B_{i}\,(k-2)!\,(-a)^{k-i}}{i!\,(k-i)!\,z^{k-1}}}=\sum _{k=i}^{\infty }{\binom {k}{i}}{\frac {B_{i}\,(-a)^{k-i}}{k\,(k-1)\,z^{k-1}}}\ .} Puisque ( k i ) = 0 {\displaystyle {\tbinom {k}{i}}=0} k < i i 2 , on peut étendre la somme ci-dessus pour k 2 (en deçà, on aurait la forme indéterminée 0/0 ) à i – 1i – 2somme vide , valide, si i = 2
B i i ( i − 1 ) z i − 1 ( 1 + a z ) − ( i − 1 ) = ∑ k = 2 ∞ ( k i ) B i ( − a ) k − i k ( k − 1 ) z k − 1 {\displaystyle {\frac {B_{i}}{i\,(i-1)\,z^{i-1}}}\left(1+{\frac {a}{z}}\right)^{-(i-1)}=\sum _{k=2}^{\infty }{\binom {k}{i}}{\frac {B_{i}\,(-a)^{k-i}}{k\,(k-1)\,z^{k-1}}}} On rappelle que les polynômes de Bernoulli vérifient :
B k ( x ) = ∑ i = 0 k ( k i ) B i x k − i = B 0 x k + k B 1 x k − 1 + ∑ i = 2 k ( k i ) B i x k − i = x k − k 2 x k − 1 + ∑ i = 2 k ( k i ) B i x k − i {\displaystyle B_{k}(x)=\sum _{i=0}^{k}{\binom {k}{i}}B_{i}\,x^{k-i}=B_{0}\,x^{k}+k\,B_{1}\,x^{k-1}+\sum _{i=2}^{k}{\binom {k}{i}}B_{i}\,x^{k-i}=x^{k}-{\frac {k}{2}}\,x^{k-1}+\sum _{i=2}^{k}{\binom {k}{i}}B_{i}\,x^{k-i}} ainsi que :
B k ( − x ) = ( − 1 ) k [ B k ( x ) + k x k − 1 ] = ( − 1 ) k B k ( x ) − k ( − x ) k − 1 {\displaystyle B_{k}(-x)=(-1)^{k}\left[B_{k}(x)+k\,x^{k-1}\right]=(-1)^{k}B_{k}(x)-k\,(-x)^{k-1}} d’où :
∑ i = 2 ∞ B i i ( i − 1 ) z i − 1 ( 1 + a z ) − ( i − 1 ) = ∑ k = 2 ∞ ∑ i = 2 ∞ ( k i ) B i ( − a ) k − i k ( k − 1 ) z k − 1 = ∑ k = 2 ∞ B k ( − a ) − ( − a ) k + k 2 ( − a ) k − 1 k ( k − 1 ) z k − 1 = ∑ k = 2 ∞ ( − 1 ) k B k ( a ) − k ( − a ) k − 1 − ( − a ) k + k 2 ( − a ) k − 1 k ( k − 1 ) z k − 1 = ∑ k = 2 ∞ ( − 1 ) k B k ( a ) − ( − a ) k − k 2 ( − a ) k − 1 k ( k − 1 ) z k − 1 = − ∑ k = 2 ∞ B k ( a ) k ( k − 1 ) ( − z ) k − 1 − [ ( z + a − 1 2 ) ln ( 1 + a z ) − a ] . {\displaystyle {\begin{aligned}\sum _{i=2}^{\infty }{\frac {B_{i}}{i\,(i-1)\,z^{i-1}}}\left(1+{\frac {a}{z}}\right)^{-(i-1)}&=\sum _{k=2}^{\infty }\sum _{i=2}^{\infty }{\binom {k}{i}}{\frac {B_{i}\,(-a)^{k-i}}{k\,(k-1)\,z^{k-1}}}=\sum _{k=2}^{\infty }{\frac {B_{k}(-a)-(-a)^{k}+{\frac {k}{2}}\,(-a)^{k-1}}{k\,(k-1)\,z^{k-1}}}\\&=\sum _{k=2}^{\infty }{\frac {(-1)^{k}B_{k}(a)-k\,(-a)^{k-1}-(-a)^{k}+{\frac {k}{2}}\,(-a)^{k-1}}{k\,(k-1)\,z^{k-1}}}\\&=\sum _{k=2}^{\infty }{\frac {(-1)^{k}B_{k}(a)-(-a)^{k}-{\frac {k}{2}}\,(-a)^{k-1}}{k\,(k-1)\,z^{k-1}}}\\&=-\sum _{k=2}^{\infty }{\frac {B_{k}(a)}{k\,(k-1)\,(-z)^{k-1}}}-\left[\left(z+a-{\tfrac {1}{2}}\right)\ln \left(1+{\tfrac {a}{z}}\right)-a\right].\end{aligned}}} Donc, pour |a | < |z | :
Γ ( z + a ) = 2 π z z + a − 1 2 exp ( − z − ∑ k = 2 ∞ B k ( a ) k ( k − 1 ) ( − z ) k − 1 ) {\displaystyle \Gamma (z+a)={\sqrt {2\pi }}\,z^{z+a-{\frac {1}{2}}}\exp \left(-z-\sum _{k=2}^{\infty }{\frac {B_{k}(a)}{k(k-1)(-z)^{k-1}}}\right)}
En posant a 0 , ½ et 1 , et connaissant les valeurs particulières des polynômes de Bernoulli en ces points, on retrouve immédiatement les équivalents en z z + ½z + 1
La première occurrence d'un produit qui donnera naissance ultérieurement à la fonction gamma est due à Daniel Bernoulli [ 11] Christian Goldbach .
En notation moderne[ 12]
x ! = lim n → ∞ ( n + 1 + x 2 ) x − 1 ∏ i = 1 n i + 1 i + x {\displaystyle x!=\lim _{n\rightarrow \infty }\left(n+1+{\frac {x}{2}}\right)^{x-1}\prod _{i=1}^{n}{\frac {i+1}{i+x}}} En 1729 également, Euler entreprend l'étude de ce produit et lui donne sa forme intégrale[ 13] , [ 14]
C'est Legendre qui, en 1811, note cette fonction Γ {\displaystyle \Gamma } [ 13] , [ 15]
L'article de Borwein et Corless[ 16]
↑ a et b Voir par exemple le début de ce devoir corrigé ↑ Pour le cas particulier où z est un réel strictement positif, voir l'article Théorème de Bohr-Mollerup . Pour le cas général, voir cet exercice corrigé ↑ (de) O. Schlömilch, « Einiges über die Eulerischen Integrale der zweiten Art », Archiv der Mathematik und Physik vol. 4, 1844 , p. 171 (lire en ligne ) ↑ (en) J. L. W. V. Jensen , « An elementary exposition of the theory of the Gamma function », Ann. of Math. 2e série, vol. 17, no 3, 1916 , p. 124-166 (JSTOR 2007272 p. 128).↑ « En 1844, 32 ans avant le célèbre travail de Weierstrass sur les fonctions entières » : (en) S. S. Dragomir, Ravi Agarwal (en) Inequalities for Beta and Gamma functions via some classical and new integral inequalities », J. Inequal. Appl. (nl) vol. 5, no 2, 2000 , p. 103-165 (lire en ligne ) p. 107).↑ (en) Jesús Guillera et Jonathan Sondow, « Double integrals and infinite products for some classical constants via analytic continuations of Lerch's transcendent », The Ramanujan Journal vol. 16, no 3, 2008 , p. 247-270 (DOI 10.1007/s11139-007-9102-0 arXiv math/0506319 ↑ (en) Karl Rawer , Wave Propagation in the Ionosphere , Dordrecht, Kluwer Academic Publishers, 1993 ↑ D'après (de) O. R. Rocktäschel, Methoden zur Berechnung der Gammafunktion für komplexes Argument , université technologique de Dresde , 1922 , thèse de doctorat ↑ (de) P. E. Böhmer, Differenzengleichungen und bestimmte Integrale , Leipzig, Köhler Verlag, 1939 ↑ (en) Serge Lang , Complex Analysis , Springer , coll. « GTM » (no 103), 1998 , 489 p. (ISBN 978-0-387-98592-3 lire en ligne ) , p. 418↑ Paul Heinrich Fuss , Correspondance mathématique et physique de quelques célèbres géomètres du XVIII e , vol. II, St. Pétersbourg, Académie impériale des sciences , 1843 (lire en ligne ) , p. 324-325↑ (en) Detlef Gronau , « Why is the gamma function so as it is? », Teaching Mathematics and Computer Science vol. 1, no 1, 2003 , p. 43-53↑ a et b G. K. Srinivasan, « The Gamma function: An Eclectic Tour », The American Mathematical Monthly vol. 114, no 4, 2007 , p. 297-315 (DOI 10.1080/00029890.2007.11920418 ↑ L. Euler, « De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt scholarlycommons.pacific.edu ↑ A.-M. Legendre, Exercices de calcul intégral sur divers ordres de transcendantes et sur les quadratures , t. 1, Vve Courcier (Paris), 1811 (lire en ligne ) , p. 221 ↑ (en) Jonathan M. Borwein et Robert M. Corless, Gamma and Factorial in the Monthly , 17 mars 2017 arXiv :1703.05349 Sur les autres projets Wikimedia :














![{\displaystyle \gamma =\sum _{k=1}^{\infty }\left[{\frac {1}{k}}-\ln \left(1+{\frac {1}{k}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7176d3dc104a5ef96f1039306f330096dde13ccd)






































![{\displaystyle \Gamma (z)={\sqrt {2\pi }}\,z^{z-{\frac {1}{2}}}{\rm {e}}^{-z}\left[1+{\frac {1}{12z}}+{\frac {1}{288z^{2}}}-{\frac {139}{51840z^{3}}}-{\frac {571}{2488320z^{4}}}+{\frac {163879}{209018880z^{5}}}+{\mathcal {O}}\left({\frac {1}{z^{6}}}\right)\right]\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/132796be4bbdfdb33be994cdfd76a06009564dc2)


![{\displaystyle \Gamma \left(z+{\frac {1}{2}}\right)={\sqrt {2\pi }}\,z^{z}{\rm {e}}^{-z}\left[1-{\frac {1}{24z}}+{\frac {1}{1152z^{2}}}+{\frac {1003}{414720z^{3}}}-{\frac {4027}{39813120z^{4}}}-{\frac {5128423}{6688604160z^{5}}}+{\mathcal {O}}\left({\frac {1}{z^{6}}}\right)\right]\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88954e14e22f4d1956713dd94139b2c00227df92)














![{\displaystyle B_{k}(-x)=(-1)^{k}\left[B_{k}(x)+k\,x^{k-1}\right]=(-1)^{k}B_{k}(x)-k\,(-x)^{k-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/363d1c480e17451907c2edbc3ca97fadc2cb84ac)
![{\displaystyle {\begin{aligned}\sum _{i=2}^{\infty }{\frac {B_{i}}{i\,(i-1)\,z^{i-1}}}\left(1+{\frac {a}{z}}\right)^{-(i-1)}&=\sum _{k=2}^{\infty }\sum _{i=2}^{\infty }{\binom {k}{i}}{\frac {B_{i}\,(-a)^{k-i}}{k\,(k-1)\,z^{k-1}}}=\sum _{k=2}^{\infty }{\frac {B_{k}(-a)-(-a)^{k}+{\frac {k}{2}}\,(-a)^{k-1}}{k\,(k-1)\,z^{k-1}}}\\&=\sum _{k=2}^{\infty }{\frac {(-1)^{k}B_{k}(a)-k\,(-a)^{k-1}-(-a)^{k}+{\frac {k}{2}}\,(-a)^{k-1}}{k\,(k-1)\,z^{k-1}}}\\&=\sum _{k=2}^{\infty }{\frac {(-1)^{k}B_{k}(a)-(-a)^{k}-{\frac {k}{2}}\,(-a)^{k-1}}{k\,(k-1)\,z^{k-1}}}\\&=-\sum _{k=2}^{\infty }{\frac {B_{k}(a)}{k\,(k-1)\,(-z)^{k-1}}}-\left[\left(z+a-{\tfrac {1}{2}}\right)\ln \left(1+{\tfrac {a}{z}}\right)-a\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f063f46e3daf79d392cd6a0fae9f091572ae41d)


