Ligne de fuite

Cet article possède un paronyme, voir La Ligne de fuite.

Dans une perspective conique, la ligne de fuite d'un plan est la figure formée par l'ensemble des points de fuite de ce plan ; les points de la ligne de fuite d'un plan représentent les directions de ce plan.

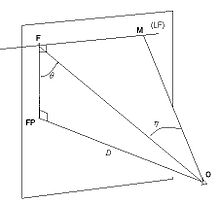
Selon Vitruve, l’artiste-peintre Agatharcos aurait mentionné la notion des lignes de fuite issues d’un centre focal unique^[1] ; pour cette raison, quelques écrivains comme Karl Woermann ont supposé qu’il aurait introduit la perspective et l'illusion dans la peinture.

Sur la figure ci-dessus, lorsque l'angle η varie le point M décrit la ligne de fuite.

On a les propriétés suivantes :

• Deux plans parallèles ont même ligne de fuite : autrement dit, deux plans parallèles paraissent se rencontrer à l'infini selon une droite ;
• La ligne de fuite d'un plan est l'intersection avec le tableau du plan parallèle passant par le point de vue : conséquence immédiate de la propriété précédente, et de ce qu'un plan passant par le point de vue est un plan « de bout », donc vu selon une droite.

Dans le cas général, la ligne de fuite d'un plan ne passe pas par le point de fuite principal de la perspective (Sur le schéma précédent, la droite FM ne passe pas par FP). Cependant, lorsque l'angle de fuite du plan, θ, est droit, la ligne de fuite passe effectivement par ce point. Une telle ligne de fuite est alors une ligne de fuite principale de la perspective.

Les plans dont la ligne de fuite est principale, c'est-à-dire les plans perpendiculaires au plan du tableau sont les plans principaux de la perspective. La ligne de fuite principale horizontale est appelée ligne d'horizon. (Attention, la dénomination d'horizon est aussi parfois utilisée pour désigner les lignes de fuite quelconques. Cependant le label horizon pour désigner la ligne de fuite principale horizontale est le plus fréquent.)

On peut voir des lignes de fuite qui ne sont pas principales sur les paysages vus en plongée: la ligne d'horizon séparant le ciel de la terre peut en effet tout à fait rester visible. C'est encore, à la rotondité de la terre près, une ligne de fuite de la perspective, mais du fait que le regard n'est plus parallèle au sol, ce n'est plus une ligne de fuite principale.

Les lignes de fuite principales possèdent trois propriétés importantes pour le dessin :

• 1- Elles passent par le point de fuite principal (définition) ;
• 2- Les directions perpendiculaires aux plans fuyant selon ces lignes conservent leur parallélisme sur la perspective. (voir le tableau de Kyoraishi sur lequel les montants verticaux et les poutres situées selon la direction droite gauche sont parallèles sur le dessin, comme elles le sont dans la réalité) ;
• 3- Les points de distance des lignes de fuite principales sont situés de part et d'autre du point de fuite principal, à une distance égale à celle du peintre au tableau.

Une ligne de fuite possède trois points particuliers :

• 1- Le point de fuite principal d'une ligne de fuite est celui situé sur une perpendiculaire au point de fuite principal de la perspective. Ce point partage la ligne en deux parties égales situées "de part et d'autre du regard" ou est à l'orthocentre lorsqu'il y a trois points de fuite ;
• 2- Les points de distance d'une ligne de fuite sont ceux des directions à 45° dans le plan d'origine. Autrement dit, si on trace un carrelage carré dont l'un des côtés est parallèle à la ligne de fuite, les diagonales du carré fuient aux points de distance (voir schéma de gauche). Ces points sont situés de part et d'autre du point de fuite et en sont éloignés, pour une perspective à l'échelle 1, d'une distance égale à celle du peintre à la ligne de fuite (voir schéma de droite).

Le fait que FF' soit égal à FO résulte de ce que le triangle FF'O est rectangle et possède un angle de 45° Il est donc rectangle isocèle. (voir figure de droite).

• 
  Mer - Gustave Courbet - La ligne d'horizon est clairement une ligne de fuite de la perspective. L'absence de lignes droites fuyant vers l'infini rend difficile d'affirmer si l'horizon est ou non ligne de fuite principale. Si vous partagez le sentiment que la mer y est peinte selon une vue en légère plongée, c'est-à-dire que l'artiste est situé sur un promontoire, alors l'horizon de ce tableau n'est pas pour vous une ligne principale.
• 
  Genshin Kyoraishi - XVIII^e siècle - Marionnettes - Les verticales étant clairement parallèles, la ligne de fuite des plans horizontaux (plafond et plancher) est une ligne de fuite principale.
• 
  Carrelage et diagonales - Les points de fuite F'' et F" sont les points de fuite des diagonales du pavage du plan. Si ce carrelage est carré, ce sont donc les points de fuite des directions qui font 45° de part et d'autre de la direction de face (direction principale). On les appelle points de distance du plan.

• Perspective conique
• Perspective (représentation)
• Perspective axonométrique
• Point de fuite

• Portail de la géométrie
• Portail de la peinture