シュレーディンガーの猫

シュレーディンガーの猫(シュレーディンガーのねこ、シュレディンガーの猫とも、英: Schrödinger's cat)は、1935年にオーストリアの物理学者エルヴィン・シュレーディンガーが発表した、猫を使った思考実験。この思考実験は、物理学的実在の量子力学的記述が不完全であると説明するために用いられた。
シュレーディンガーは、EPR論文を補足する論文の中で、観測されない限り重ね合わせであるとして記述すると、巨視系の状態が"状態見分けの原理"(巨視的な観測をすれば区別できる巨視系の諸状態は、観測の有無にかかわらず区別できるとする原理)を満たさないことを示す具体例として、この思考実験を用いた[1]。
前史・背景
[編集]ニュートン以来の古典物理学においては、「最初の条件さえ決まれば、以後の物質の状態や運動はすべて確定される」と考えられている(決定論)[2]。量子論の場合、物理法則を決定論的にするには隠れた変数の存在が必要である[3]。
19世紀末から20世紀初頭に始まった量子論ないし量子力学は、1926年にエルヴィン・シュレーディンガーが波動方程式を導出し、さらにシュレーディンガー方程式(波動関数)によって量子の状態を確率的に定めることができる数式を発見した[4]。これは重要な発見と見なされたが、あくまで確率的に予想するという考え(非決定論)は、それまでの物理学の考えに反し、シュレーディンガー自身、量子の状態は決定論的に予想することが可能で、この理論はまだ途上であると考えていた。当時の多くの物理学者達も共通の考えでもあった[5]。
その後1927年にヴェルナー・ハイゼンベルクは不確定性原理を発表した。これについて佐藤勝彦は、量子の状態はそもそも不確定的ないし確率的であり、事象は重なり合った状態で存在し、それを人間が観測することによって事象が収縮して結果が定まるという常識を覆す理論であったと説明する[5]。すなわち波動関数は、それ自体で既に完成しているのであり、量子の状態を決定論的に表すことはできないというものであった。マクロの世界の法則とは全く異なるという批判に対し、量子力学者たちは、ミクロの世界の特殊性を挙げて反論した。ジョン・フォン・ノイマンは自著『量子力学の数学的基礎』において、隠れた変数理論の否定的証明を行い(ノイマンのNO-GO定理)、計算上で観測時に観測結果を選びとる射影公準を提唱し、観測する側とされる側の境界をどこにでも設定できるとした。
こうした情勢の中で1935年にシュレーディンガーが発表した思考実験が後に「シュレーディンガーの猫」と呼ばれるものとなった[6]。
猫の生死に関する思考実験
[編集]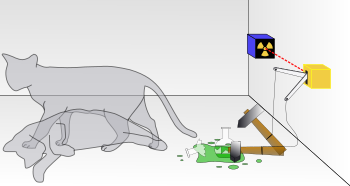
1935年、シュレーディンガーはドイツ科学誌上で論文『量子力学の現状について』を発表し、射影公準における収縮がどの段階で起きるのかが明確でないことによって引き起こされる矛盾を示した[7]。一方で、佐藤勝彦は、その中で猫を使った思考実験を用いて、ミクロの世界に特有な確率解釈の矛盾を突くことで、量子力学が未だ不完全な学問であることを証明しようとしたとしている[6]。実験の内容は以下のとおりである。
猫と放射性元素のある密閉した鋼鉄の箱の中で、放射性元素の1時間あたりの原子の放射性崩壊確率を50%とし、ガイガー計数管が原子崩壊を検知すると電気的に猫が殺される仕掛けにすると、1時間経過時点における原子の状態を表す関数は
|原子の状態|=|放射線を放出した|+|放射線を放出していない|
という二つの状態の50%ずつの重ね合わせによって表される。その結果、猫の生死は、
|箱の中の状態|=|(放射線が放出されたので)猫が死んでいる|+|(放射線が放出されていないので)猫は生きている|
という50%ずつの重ね合わせの状態になり、箱の中では箱を開けてそれを確認するまで猫が死んでいる状態と生きている状態の重ね合わせになる。もしもこれが現実を記述しているとすれば、「巨視的な観測をする場合には、明確に区別して認識される巨視的な系の諸状態は、観測がされていてもいなくても区別される」という“状態見分けの原理”と矛盾する。シュレーディンガーはこのことをもって、量子力学的記述は未完成であると主張した[1]。
蓋のある密閉状態の箱を用意し、この中に猫を1匹入れる。箱の中には他に少量の放射性物質とガイガーカウンター、それで作動される青酸ガスの発生装置がある。放射性物質は1時間の内に原子崩壊する可能性が50%であり、もしも崩壊した場合は青酸ガスが発生して猫は死ぬ。逆に原子崩壊しなければ毒ガスは発生せず猫が死ぬことはない。「観測者が箱を開けるまでは、猫の生死は決定していない」とされている[6]。原子がいつ崩壊するのかは量子力学的には確率的にしか説明することができない。観測者が見るまでは、箱の中の原子が崩壊している事象と崩壊していない事象は重なり合って存在している。観測者が確認をした瞬間に事象が収縮して結果が定まる。シュレーディンガーはこれを「猫の生死」という事象に結び付け、「観測者が箱の中身を確認するまでは、猫の生死は確定しておらず(非決定)、観測者が蓋を開けて中を確認した時に初めて事象が収縮して、それにより猫の生死が決まるとして、箱を開けるまでは、生きている猫の状態と死んだ猫の状態が重なり合って存在している」という意味に解釈し[6]、「ミクロの世界の特殊性」を前提にした量子力学者たちの説明に対して、「マクロの事象」を展開することによって「量子力学の確率解釈」が誤っていることを証明しようとした[6]。
解決策
[編集]現場の物理学者はシュレーディンガーの猫のようなことに思い悩むことはないとヒラリー・パトナムは1965年に指摘している。なぜなら現場の物理学者は、量子力学とは別の付加的な仮定として巨視的な可観測量が常に明確な値を保持する原理を受け入れており、この原理を元に測定がいつ起こらなければならないかを導き出しており、その結果として波動関数の収縮は巨視的な重ね合わせが予想される直前に起きるべきとの立場をとる、とパトナムは説明する[1][8]。
ニールス・ボーアは、観測者によって波動関数の収縮が引き起こされるという考えを用いず、完全に客観的とみなせる測定装置と対象との間の相互作用について論じた[9]。そしてその相互作用の不可逆性を強調した[9]。ボーアにとって、箱が開けられる前から猫は生きているか死んでいるかのどちらかであり、重ね合わせではない[9][10]。なお、射影公準を提唱したジョン・フォン・ノイマンは、1932年の著書 『量子力学の数学的基礎』において、物心並行論は「科学的世界観にとって基本的な要請」であり、それを満足するには実験系と測定側の境界をどこにでも置けなければならないとしている[11]。
量子測定理論
[編集]量子測定理論では、理想測定と見なせる境目(ハイゼンベルク切断)までは観測装置も量子論に従う系の一部として扱い、そこから先の測定系は射影公準により遮断できるとされており[12][13][7]、渡部鉄兵は、猫の運命はアルファ粒子とガイガーカウンターの相互作用が終了する時刻に決まるとしている[7]。なお、渡部は、観測問題の解決手段として、観測者の知覚が波束の収縮を引き起こして猫の生死が決定するという解釈への批判がこの思考実験だとしている[7]。
量子デコヒーレンス
[編集]粒子検出器が反応すると同時にデコヒーレンスが起きて、その時点で猫の生死が確定する。デコヒーレンスは多世界解釈に導入されており、猫が生きている状態と死んでいる状態の重ね合わせはデコヒーレンスによって異なる世界に分岐したとみなせる[14]。一方の世界の観測者は箱を開けたとき生きている猫を見て、もう一方の世界の観測者は死んだ猫を見る。
その他の解釈
[編集]決定論的な隠れた変数理論では、猫がいつ死ぬか(または死なないか)は初めから決まっている。ただ観測者が隠れた変数を知らないため、不確定性が存在するように見える。
自発的収縮理論では、観測とは無関係に波動関数が収縮する。一つ一つの粒子の状態が収縮するのは非常に稀だが、多数の粒子が集まることで瞬間的に収縮が起きる。そのためマクロな物体の重ね合わせは生じない。猫の思考実験に当てはめると、粒子検知器の時点で波動関数が収縮するため、猫の重ね合わせ状態は生じない。
哲学への影響
[編集]この思考実験は哲学の次の二つの分野でもしばしば議題に上り、一つは量子力学の解釈問題の議論の前提となる科学的定義に関する科学哲学においてであり[15]、量子力学の理論的枠組みが、従来の科学哲学に基づいた定義にそぐわないことを指摘する上で、この思考実験が引用されている。もう一つは心の哲学において心の因果作用(「物理領域の因果的閉鎖性」参照)を議論するに際して、量子力学の確率過程が問題となってくる場合においてである[16]。
大衆文化における登場
[編集]シュレーディンガーの猫およびそれをモチーフとした設定やフレーズは、SFのみならず、ミステリを含めた創作に多数登場する。
2010年代にはフランスの作家フィリップ・フォレストが長編小説『シュレーディンガーの猫を追って』を発表した[17]。
日本における流行については、自作『異次元の館の殺人』で使用している作家芦辺拓が、日本人好みの無常観が背景にあるのではないかと指摘している[18]。
タイムマシンをテーマにした人気ゲーム「Steins;Gate」においても、主人公が観測した事象が事実として扱われるという設定であり、作中において「シュレーディンガーの猫」の説明がなされる。
脚注
[編集]出典
[編集]- ^ a b c マックス・ヤンマー著/井上健訳『量子力学の哲学』pp. 251-261
- ^ 佐藤 2000, pp. 140–141, 174.
- ^ 佐藤 2000, pp. 177–178.
- ^ 佐藤 2000, pp. 117–121.
- ^ a b 佐藤 2000, pp. 140–144
- ^ a b c d e 佐藤 2000, pp. 191–201
- ^ a b c d 白井仁人、東克明、森田邦久、渡部鉄兵『量子という謎 量子力学の哲学入門』(勁草書房 2012年 ISBN 978-4-326-70075-2)pp. 3-16
- ^ Putnam, Hilary. "A philosopher looks at quantum mechanics." Beyond the edge of certainty 2 (1965): 75-101.
- ^ a b c Faye, Jan [in 英語] (6 December 2019). "Copenhagen Interpretation of Quantum Mechanics". Stanford Encyclopedia of Philosophy (英語). The Metaphysics Research Lab Center for the Study of Language and Information, Stanford University. 2022年1月30日閲覧。
- ^ ヘリガ・カーオ『20世紀物理学史【上巻】―理論・実験・社会』名古屋大学出版会 、2015年、p. 282
- ^ J.v.ノイマン、広重徹『量子力学の数学的基礎』井上健、恒藤敏彦 翻訳、みすず書房、1957年11月15日、333頁。ISBN 978-4622025092。
- ^ Modern Theory of Quantum Measurement and its Applications清水明/東京大学大学院
- ^ 「量子測定の原理とその問題点」清水明/数理科学NO.469,JULY 2002
- ^ ショーン・キャロル『量子力学の奥深くに隠されたもの コペンハーゲン解釈から多世界理論へ』青土社、2020年、pp. 298-302
- ^ 高林武彦 著、保江邦夫 編『量子力学 観測と解釈問題』海鳴社 2001年 ISBN 4-87525-204-8
- ^ デイヴィッド・チャーマーズ 著、林一 訳『意識する心』(2001年、ISBN 4-8269-0106-2) pp. 407-435「量子力学の解釈」
- ^ 海老沢類 (2017年11月15日). “長編「シュレーディンガーの猫を追って」仏作家・フィリップ・フォレストさん 喪失の痛みと生きる”. 産経ニュース. 産経新聞社. 2022年9月2日閲覧。
- ^ "(扉)シュレーディンガーの猫、エンタメ彩る ありえた世界は「今を変える希望」:朝日新聞デジタル". 朝日新聞 (朝刊 ed.). 朝日新聞社. 2021年5月30日. p. 裏面. 2022年10月5日閲覧。
参考文献
[編集]- 『「量子論」を楽しむ本 ミクロの世界から宇宙まで最先端物理学が図解でわかる!』佐藤勝彦 監修、PHP研究所〈PHP文庫〉、2000年4月3日。ISBN 978-4-56-957390-8。
