メタ

ウィキペディアについての議論を行う「メタウィキ」についてはWikipedia:メタウィキメディアをご覧ください。

「メタ」のその他の用法については「メタ (曖昧さ回避)」をご覧ください。

ウィクショナリーに関連の辞書項目があります。

メタ、en:meta-

メタ（meta-、 古希: μετὰ-) とは、以下の意味を持つ接頭辞である：

一般的な意味

• 「あとに」という意味の古代ギリシャ語の接頭辞^[1]。
• 転じて「超越した」、「高次の」という意味の接頭辞で^[2]、ある学問や視点の外側にたって見る事を意味する^[1]。
• 「変化」を意味する接頭辞。例えば metamorphose（変化）、metabolism（代謝）などで用いられる^[3]。

化学における意味

• ベンゼン環の2置換体の構造異性体のうち、2つの置換基が炭素原子1つをはさんでいるものにつける接頭辞^[2]。
• 同じ酸化物を水和して得られるオキソ酸の中で、水和度の低いものにつける接頭辞^[2]。

「ある学問や視点の外側にたって見る」という意味はアリストテレスの著書『メタピュシカ』（形而上学）に由来しており^[1]、哲学では他にも「メタ倫理学」、「メタ哲学」等の用例がある。

数学基礎論や数理論理学では、数学や論理学を（人工）言語とみなした上で数学的手段を用いて研究としているので、研究対象たる「数学」や「論理学」のような「言語」と、それらの研究対象を研究するために用いる「数学」、「論理学」、「言語」を分けて考える必要があり、後者をそれぞれ「メタ数学」（英: metamathematics、超数学とも訳される）「メタ論理」、「メタ言語」と呼ぶ。またメタ数学やメタ言語等に関する概念には「メタ」という接頭辞を用い、例えばメタ数学の定理を研究対象の数学の定理と区別し、「メタ定理」（英: metatheorem）と呼ぶ。より一般に、これらの例のように何らかの理論（上では「数学」や「論理学」）を研究するための理論を一般に「メタ理論」と呼ぶ。

数理論理学をその始祖の一つとして持ち、人工言語たるプログラミング言語を研究対象の一つとして持つ計算機科学でも、「メタデータ」「メタプログラミング」「メタタグ」「メタヒューリスティクス」「メタ構文変数」「メタ検索エンジン」「メタファイル」「メタクラス」等の用例がある。

他にも「メタ認知」「メタ知識」「メタ記憶」「メタアナリシス」「メタデザイン」「メタモデル」「メタメッセージ」「メタ法価値論」「メタフィクション」等の用例がある。

「メタ」は元来は古代ギリシャ語で「あとに」という意味で^[1]、線文字Bで書かれたミケーネ・ギリシャ語での用例が最古のものである^[4]。この元来の意味も学術用語で使われる事があり、例えばMetatheria（後獣下綱）は、生物の分類を木で表したときTheria（獣亜綱）のあとに来る事による命名である。

「超越した」、「高次の」という意味で「メタ」が用いられるようになったのはアリストテレスの『タ・メタ・タ・ピュシカ』（古希: τὰ μετὰ τὰ φυσικά、直訳は『自然に関するものの後に』^[1]だが、通常は『形而上学』と訳される）という書物に起源を持つ^[1]。

本書が編集された際、自然学的な著作の後に置かれた事からこの名称で呼ばれたと思われるが^[1]、後世になって本書がその短縮形『メタピュシカ』（古希: Μεταφυσικά）で呼ばれるようになるとこの本来の意味は忘れられ、「自然学を越えたもの」という意味に解されるようになった^[1]。

オックスフォード英語辞典によれば、「～を超えて」、「～について」といった意味で「メタ」を英語で用いたのは1917年に遡り、数理論理学に関連する単語で用いられるようになったのは1929年以前である。1920年にはヒルベルトが「メタ数学」という単語を用いている。また1937年にはクワインが「メタ定理」という単語を用いている^[5]。

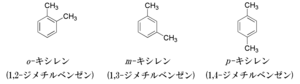
ベンゼン環の2置換体の構造異性体のうち、2つの置換基が炭素原子1つをはさんでいるものにメタ（meta-、イタリックで、ハイフンをつける）をつける。言い換えれば、1位と3位の炭素原子に置換基があるものである（隣り合う番号は他にもあるが、命名規則により1位と3位となる）。m- と略して書く。

メタに対し、隣（1位と2位）をオルト (ortho- , o-) 、反対側（1位と4位）をパラ (para- , p-) という。

また、ある置換基に注目したとき、その二つ隣の位置をメタ位と呼ぶ。

同じ酸化物を水和して得られるオキソ酸の中で水和度の低いものに、メタ（meta、ハイフンはつけず一語にする）をつける。

メタリン酸、メタホウ酸など。

1. ^ ^{a b c d e f g h} 山口義久「第五章「実態と本質」†『形而上学』とメタの視点」『アリストテレス入門』〈ちくま新書〉2019年10月9日、位置1113（kindle版）頁。ASIN B00G949N9A。ISBN 978-4480059017。 
2. ^ ^{a b c} “メタ（meta）の意味”. goo辞書. goo国語辞書. NTT Resonant Inc.. 2020年8月10日閲覧。 “出典：デジタル大辞泉（小学館）”
3. ^ “Cambridge Dictionary "Meta"”. 2020年8月14日閲覧。
4. ^ “The Linear B word me-ta”. Palaeolexicon.com. 2020年8月13日閲覧。
5. ^ Willard Van Orman Quine, "Logic Based on Inclusion and Abstraction", The Journal of Symbolic Logic, Vol. 2, No. 4, pp. 145–152, December 1937