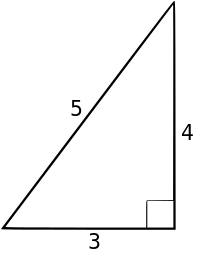
直角三角形 ABC の斜辺は線分 AB で、その長さは c である。 斜辺 (しゃへん、hypotenuse)とは、直角三角形 において、直角 に対する辺 のことである。直角三角形の斜辺は三辺の中で最も長く、その長さはピタゴラスの定理 により求めることができる。
英語のhypotenuse という言葉は、ギリシア語で「下」という意味のhypo- と「延ばす」という意味のteinein [ 1] tenuse [ 2] hypoteinousa )という言葉に由来すると言われている。
和算 においては直角三角形のことを勾股弦、斜辺のことを弦(げん)という[ 3] [ 4]
直角を挟む二辺の長さが3mと4mであるとき、斜辺の長さは5mとなる。 図の直角三角形 ABC において、斜辺の長さ c は直角を挟む二辺の長さ a, b から定まり、平方根 を用いると
c = a 2 + b 2 {\displaystyle c={\sqrt {a^{2}+b^{2}}}} と書ける。
^ Schwartzman, Steven The Words of Mathematics, An Etymological Dictionary of Mathematical Terms used in English , Published by the Mathematical Association of America. ^ Anderson, Raymond (1947). Romping Through Mathematics . Faber. pp. 52 ^ 精選版 日本国語大辞典『勾股弦・鉤股弦 』 - コトバンク ^ 日本大百科全書(ニッポニカ)『規矩術 』 - コトバンク