Коэффициент зацепления

Коэффициент зацепления — целочисленная характеристика пары пространственных замкнутых кривых без пересечений и самопересечений, описывающая суммарное количество раз, которое одна кривая в определённом смысле зацепляется за другую.

Коэффициент зацепления является важным топологическим понятием, которое естественно возникает в теории узлов, в квантовой механике, в явлении электромагнитного взаимодействия и при сверхспирализации ДНК.

С помощью инструментов алгебраической топологии возможно придать коэффициенту зацепления различные интерпретации и обобщить его на произвольную размерность.

Понятие коэффициента зацепления было введено Карлом Фридрихом Гауссом в краткой заметке на странице его личного дневника^[1], датированной 22 января 1833 года. Коэффициент зацепления допускает множество различных определений, эквивалентность которых не вполне очевидна. В простейшем случае, если одна из кривых лежит в некоторой плоскости, то коэффициент зацепления равен, грубо говоря, суммарному количеству раз, которое вторая кривая протыкает плоскую область, ограниченную первой кривой:

				⋯
коэффициент зацепления 0	коэффициент зацепления 1	коэффициент зацепления 2	коэффициент зацепления 3

Точнее, в определении коэффициента зацепления протыкания необходимо учитывать «со знаком»: приходящие с одной из сторон плоской области подсчитываются со знаком плюс, а приходящие с другой — со знаком минус. Таким образом, коэффициент зацепления учитывает направление обхода кривой и может принимать отрицательные значения:

			⋯
	коэффициент зацепления −1	коэффициент зацепления −2

В общем случае, когда не обязательно одна из кривых лежит в некоторой плоскости, простейший подход к точному определению коэффициента зацепления предоставляет теория узлов.

Пусть двухкомпонентное зацепление задано плоской диаграммой, подобной изображенным выше. Предположим, что зацепление ориентировано, то есть на каждой его компоненте указано направление. Разобьём перекрёстки диаграммы на два типа, назвав перекрёсток положительным, если направление его нижней ветви указывает налево от направления его верхней ветви, и отрицательным, если направо:

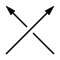положительный перекрёсток	отрицательный перекрёсток

Коэффициент зацепления, по определению, равен половине разности между количеством ${\displaystyle M}$ положительных перекрёстков, в которых фигурируют две различные компоненты зацепления, и количеством ${\displaystyle N}$ отрицательных таких перекрёстков^[2]:

${\displaystyle {\text{коэффициент зацепления}}={\frac {M-N}{2}}.}$

Коэффициент зацепления возможно определить и для неориентированных зацеплений. Поскольку при обращении ориентации одной из компонент типы перекрёстков, фигурирующих в определении чисел ${\displaystyle M}$ и ${\displaystyle N}$, меняются местами, сам коэффициент зацепления меняет свой знак, и, таким образом, его абсолютное значение является корректно определённой характеристикой неориентированных двухкомпонентных зацеплений.

Аналогичные соображения показывают, что коэффициент зацепления меняет знак при зеркальном отражении ориентированного зацепления.

Важнейшим свойством коэффициента зацепления является то, что он не изменяется при непрерывной деформации кривых^[3]. Иными словами, результат его вычисления не зависит от выбора конкретного представителя зацепления и его диаграммы и, тем самым, он представляет собой инвариант двухкомпонентных ориентированных зацеплений. Кроме того, он является инвариантом степени один^[4].

Непосредственно из определения коэффициента зацепления следует, что он не изменяется при переключении типа такого перекрёстка, в котором фигурируют ветви одной и той же компоненты. Верен и более общий факт: коэффициенты зацепления гомотопных зацеплений совпадают^[5]. Это следует, например, из представленной ниже интерпретации коэффициента зацепления в виде степени отображения Гаусса➤. А именно, отображения Гаусса гомотопных зацеплений гомотопны, а степени гомотопных отображений совпадают.

Коэффициент зацепления принадлежит семейству инвариантов Милнора. Более того, он является полным инвариантом гомотопических классов двухкомпонентных ориентированных зацеплений^[6]. Иными словами, два таких зацепления гомотопны тогда и только тогда, когда их коэффициенты зацепления совпадают.

Свойство инвариантности относительно непрерывной деформации позволяет заключить, что если двухкомпонентное зацепление является разводимым, то его коэффициент зацепления равен нулю. Это связано с тем, что разводимое зацепление, по определению, имеет диаграмму, на которой две компоненты не имеют общих перекрёстков.

Стоит отметить, что обратное утверждение в общем случае неверно — зацепление Уайтхеда имеет нулевой коэффициент зацепления, но неразводимо.

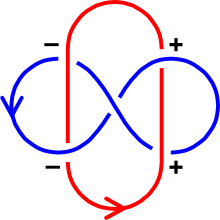
Имеется следующий альтернативный способ подсчёта коэффициента зацепления. Покрасим одну компоненту ориентированной диаграммы в синий цвет, а другую — в красной. Тогда каждый её перекрёсток имеет один из следующих четырёх типов:

Обозначим символами ${\displaystyle n_{1}}$, ${\displaystyle n_{2}}$, ${\displaystyle n_{3}}$ и ${\displaystyle n_{4}}$ количества перекрёстков каждого из четырёх типов. Иными словами, ${\displaystyle n_{1}}$ — количество положительных перекрёстков, на которых красная компонента проходит под синей, ${\displaystyle n_{2}}$ — количество положительных перекрёстков, на которых красная компонента проходит над синей, и так далее. Тогда выполняется соотношение^[7] ${\displaystyle n_{1}+n_{3}=n_{2}+n_{4}}$. В частности,

${\displaystyle {\text{коэффициент зацепления}}={\frac {(n_{1}+n_{2})-(n_{3}+n_{4})}{2}}=n_{1}-n_{4}=n_{2}-n_{3}.}$

Таким образом, вместо того, чтобы перебирать все общие перекрёстки двух компонент, достаточно смотреть либо только на перекрёстки, в которых красная компонента является нижней ветвью (разность ${\displaystyle n_{1}-n_{4}}$), либо только на перекрёстки, в которых красная компонента является верхней ветвью (разность ${\displaystyle n_{2}-n_{3}}$).

Пусть ${\displaystyle \gamma _{1},\gamma _{2}\colon S^{1}\to \mathbb {R} ^{3}}$ — гладкие вложения окружности в трёхмерное евклидово пространство, параметризующие компоненты заданного зацепления. Зададим гладкое отображение ${\displaystyle \Gamma \colon S^{1}\times S^{1}\to S^{2}}$ из тора в единичную сферу формулой

${\displaystyle \Gamma (x,y)={\frac {\gamma _{2}(x)-\gamma _{1}(y)}{|\gamma _{2}(x)-\gamma _{1}(y)|}}}$.

Иными словами, сопоставим каждой паре точек на компонентах зацепления вектор единичной длины, указывающий от первой точки к второй. Функция ${\displaystyle \Gamma }$ называется отображением Гаусса^{[8][комментарий 1]}. Утверждается, что степень этого отображения совпадает, с точностью до знака, с коэффициентом зацепления исходных кривых^[2][9]. Иными словами, их абсолютные значения равны.

Наглядное объяснение данного совпадения может быть получено обращением к определению степени гладкого отображения через анализ прообразов маленькой окрестности его некоторого регулярного значения. В качестве такого регулярного значения можно выбрать вектор ${\displaystyle (0,0,1)\in S^{2}}$, который ортогонален плоскости диаграммы зацепления. Так, равенство ${\displaystyle \Gamma (x,y)=(0,0,1)}$ выполняется в том и только в том случае, если точки ${\displaystyle x}$ и ${\displaystyle y}$ образуют на диаграмме перекрёсток, на котором вторая компонента является верхней ветвью. Кроме того, тип такого перекрёстка (то есть идёт нижняя ветвь налево или направо от верхней) зависит от того, сохраняет или обращает ориентацию тора и сферы ограничение отображения Гаусса на маленькую окрестность пары ${\displaystyle (x,y)}$. Тем самым, величина ${\displaystyle n_{2}-n_{3}}$ совпадает (с точностью до знака, зависящего от выбора ориентаций тора и сферы) со степенью отображения Гаусса.

Пусть ${\displaystyle r_{1},r_{2}\colon [0,2\pi ]\to \mathbb {R} ^{3}}$ — гладкие отображения, параметризующие компоненты заданного зацепления. Степень отображения Гаусса, соответствующая этому зацеплению, допускает выражение^[8]

${\displaystyle {\textrm {deg}}(\Gamma )={\dfrac {1}{4\pi }}\int _{0}^{2\pi }\int _{0}^{2\pi }{\frac {r_{2}(t)-r_{1}(s)}{|r_{2}(t)-r_{1}(s)|^{3}}}\cdot [{\dot {r}}_{1}(s)\times {\dot {r}}_{2}(t)]\,ds\,dt,}$

где символ ${\displaystyle \times }$ обозначает векторное произведение, а символ ${\displaystyle \cdot }$ — скалярное. Иными словами, подынтегральное выражение представляет собой смешанное произведение отображения Гаусса и производных параметризаций компонент. Интеграл, тем самым, вычисляет суммарную площадь «со знаком» образа относительно отображения Гаусса тора на сфере.

Данная интерпретация коэффициента зацепления называется интегральной формулой Гаусса^[10] и электромагнитной формулой Гаусса^[11]. Обозначая ${\displaystyle r_{1}=(x,y,z)}$ и ${\displaystyle r_{2}=(x^{\prime },y^{\prime },z^{\prime })}$, выражение выше приобретает вид^[9]

${\displaystyle {\textrm {deg}}(\Gamma )={\dfrac {1}{4\pi }}\int \int {\frac {(x^{\prime }-x)(dydz^{\prime }-dzdy^{\prime })+(y^{\prime }-y)(dzdx^{\prime }-dxdz^{\prime })+(z^{\prime }-z)(dxdy^{\prime }-dydx^{\prime })}{[(x^{\prime }-x)^{2}+(y^{\prime }-y)^{2}+(z^{\prime }-z)^{2}]^{3/2}}},}$

в котором Гаусс изначально и сформулировал свою формулу для коэффициента зацепления^[12].

Коэффициент зацепления возможно следующим образом вычислить в терминах первой группы гомологий.

Пусть ${\displaystyle K}$ — образ гладкого вложения ${\displaystyle \gamma _{1}\colon S^{1}\to \mathbb {R} ^{3}}$, параметризующего первую компоненту зацепления. Тогда параметризация ${\displaystyle \gamma _{2}\colon S^{1}\to \mathbb {R} ^{3}}$ второй компоненты зацепления задаёт петлю в дополнении узла ${\displaystyle K}$. Первая группа гомологий дополнения любого узла является бесконечной циклической, следовательно, можно выбрать её образующую ${\displaystyle x\in H_{1}(\mathbb {R} ^{3}\backslash K)}$ и число ${\displaystyle n\in \mathbb {Z} }$ такие, что ${\displaystyle [\gamma _{2}]=nx}$, где символ ${\displaystyle [a]}$ обозначает гомологический класс петли ${\displaystyle a}$. Тогда число ${\displaystyle n}$ совпадает, с точностью до знака, с коэффициентом зацепления исходных кривых^[13][14].

Коэффициент зацепления возможно следующим образом вычислить в терминах поверхностей Зейферта.

Выберем такую поверхность Зейферта для одной из компонент зацепления, что она пересекает вторую компоненту трансверсально в конечном числе точек. Ориентации поверхности и второй компоненты позволяют разбить все такие пересечения на два типа, следуя правилу буравчика. Тогда коэффициент зацепления равен суммарному количеству «со знаком» подобных протыканий поверхности второй компонентой^{[2][15][13][14]}. Иными словами, он равен алгебраическому индексу пересечения поверхности Зейферта и второй компоненты.

Например, если одна из компонент зацепления имеет поверхность Зейферта, не пересекающуюся с другой компонентой, то коэффициент зацепления равен нулю. В частности, если коэффициент зацепления не равен нулю, то зацепление не является ограничивающим^[16]. Стоит отметить, что верно и обратное к первому утверждению: если коэффициент зацепления равен нулю, то каждая компонента имеет поверхность Зейферта, не пересекающуюся с другой компонентой^[17]. Сами эти поверхности, впрочем, могут пересекаться.

Коэффициент зацепления может быть определён для произвольной пары непрерывных отображений связных замкнутых ориентируемых многообразий ${\displaystyle M^{n}}$ и ${\displaystyle N^{m}}$ размерностей ${\displaystyle n}$ и ${\displaystyle m}$, где ${\displaystyle n,m\in \{0,1,2,\ldots \}}$, в евклидово пространство ${\displaystyle \mathbb {R} ^{n+m+1}}$, образы которых не пересекаются. Один из возможных подходов — обратиться к прямому аналогу отображения Гаусса

${\displaystyle M^{n}\times N^{m}\to S^{n+m}}$

и положить коэффициент зацепления равным его степени^[18][19]. Отметим, что степень зависит от выбора ориентаций в ${\displaystyle M^{n}\times N^{m}}$ и ${\displaystyle S^{n+m}}$.

Например, коэффициент зацепления пары точек в ${\displaystyle \mathbb {R} ^{1}}$ указывает на то, в каком порядке они расположены на прямой, а коэффициент зацепления точки и не проходящей через неё замкнутой кривой в ${\displaystyle \mathbb {R} ^{2}}$ равен порядку этой точки относительно этой кривой.

Аналогично случаю пар непересекающихся замкнутых кривых в трёхмерном пространстве доказывается, что коэффициент зацепления инвариантен относительно гомотопий, в процессе которых образы остаются непересекающимися.

Подход к вычислению коэффициента зацепления замкнутых кривых с помощью поверхностей Зейферта имеет аналог и в данном контексте многообразий. В следующем разделе он является отправной точкой к определению коэффициента зацепления в многообразиях, отличных от евклидова пространства ${\displaystyle \mathbb {R} ^{n}}$.

Коэффициент зацепления может быть определён для пар непрерывных отображений замкнутых ориентированных многообразий ${\displaystyle M^{n}}$ и ${\displaystyle N^{m}}$ размерностей ${\displaystyle n}$ и ${\displaystyle m}$ в произвольное ориентированное многообразие ${\displaystyle L^{n+m+1}}$ размерности ${\displaystyle n+m+1}$, образы которых не пересекаются. В данном определении многообразия ${\displaystyle M^{n}}$ и ${\displaystyle N^{m}}$ необязательно связны.

Предположим, что образ ${\displaystyle M^{n}}$ в ${\displaystyle L^{n+m+1}}$ является образом края непрерывного отображения некоторого ориентированного многообразия ${\displaystyle T^{n+1}}$ размерности ${\displaystyle n+1}$. Тогда можно положить коэффициент зацепления равным алгебраическому индексу пересечения образа ${\displaystyle T^{n+1}}$ и образа ${\displaystyle N^{m}}$. В случае, когда образ ${\displaystyle N^{m}}$ сам является образом края некоторого ориентированного многообразия на единицу большей размерности, от выбора ${\displaystyle T^{n+1}}$ данная величина не зависит^[20]. В случае ${\displaystyle L^{n+m+1}=\mathbb {R} ^{n+m+1}}$ указанный индекс пересечения совпадает с коэффициентом зацепления, введённым ранее.

Например, пусть на сфере с ручками имеется набор заряженных точек (то есть точек с предписанными целыми числами) и не проходящая через них простая ориентированная замкнутая кривая. Чтобы кривая ограничивала двумерное многообразие, необходимо и достаточно того, чтобы она была разделяющей. А чтобы набор точек ограничивал одномерное многообразие, необходимо и достаточно, чтобы сумма их зарядов была равна нулю. В случае, если данные условия выполняются, коэффициент зацепления равен сумме зарядов тех точек, которые попали в одну из областей, ограниченных кривой (какую именно — зависит от ориентации кривой). Таких областей две, а соответствующие суммы всегда отличаются знаком.

Из приведённого выше определения коэффициента зацепления видно, что при замене одного из отображений на гомологичное (в дополнении образа второго отображения до всего многообразия) коэффициент зацепления не меняется^{[комментарий 2]}. Поэтому его естественно рассматривать в контексте теории гомологий, а именно, следующего варианта определения.

Пусть ${\displaystyle x^{n}}$ и ${\displaystyle y^{m}}$ — пара непересекающихся циклов размерностей ${\displaystyle k-1}$ и ${\displaystyle n-k}$ в ${\displaystyle L^{n+m+1}}$. Предположим, что цикл ${\displaystyle x^{n}}$ гомологичен нулю. Иными словами, он является границей некоторого цикла ${\displaystyle z^{n+1}}$ размерности ${\displaystyle n+1}$. Тогда можно положить коэффициент зацепления равным алгебраическому индексу пересечения циклов ${\displaystyle z^{n+1}}$ и ${\displaystyle y^{m}}$. В случае, когда цикл ${\displaystyle y^{m}}$ сам гомологичен нулю, от выбора цикла ${\displaystyle z^{n+1}}$ данная величина не зависит^[20].

Приведённая выше конструкция построения коэффициента зацепления допускает следующее дальнейшее обобщение. Предположим теперь, что некоторое кратное цикла ${\displaystyle x^{n}}$ гомологично нулю. Иными словами, существует такая цепь ${\displaystyle z^{n+1}}$ размерности ${\displaystyle n+1}$, что ${\displaystyle \partial z^{n+1}=ax^{n}}$ для некоторого ненулевого ${\displaystyle a\in \mathbb {Z} }$. Тогда можно положить коэффициент зацепления равным рациональному числу ${\displaystyle b/a}$, где ${\displaystyle b}$ — алгебраический индекс пересечения циклов ${\displaystyle z^{n+1}}$ и ${\displaystyle y^{m}}$. В случае, когда некоторое кратное цикла ${\displaystyle y^{m}}$ само гомологично нулю, от выбора цикла ${\displaystyle z^{n+1}}$ указанная величина не зависит^[21].

Построенная характеристика не всегда симметрична — при замене циклов ${\displaystyle x^{n}}$ и ${\displaystyle y^{n}}$ местами она может изменить знак^[22], а именно, умножается на ${\displaystyle (-1)^{n(m+1)}}$.

При замене одного из циклов на гомологичный цикл коэффициент зацепления может измениться на целое число. Это связано с тем, что такая гомология может сама иметь со вторым циклом ненулевой коэффициент зацепления^[22]. Поэтому каждым двум гомологическим классам из подгрупп кручения групп гомологий ${\displaystyle H_{n}(L^{n+m+1})}$ и ${\displaystyle H_{m}(L^{n+m+1})}$ можно корректно сопоставить рациональное число, рассматриваемое по модулю своей целой части. Таким образом, имеется спаривание, представляющее собой билинейное отображение абелевых групп

${\displaystyle \operatorname {Tor} H_{n}(L^{n+m+1})\times \operatorname {Tor} H_{m}(L^{n+m+1})\to \mathbb {Q} /\mathbb {Z} ,}$

которое называется формой зацепления. Оно является невырожденным в смысле двойственности Пуанкаре. Данный факт является примером так называемой двойственности Понтрягина.

В частном случае ${\displaystyle n=m}$ получается билинейная форма

${\displaystyle \operatorname {Tor} H_{n}(L^{2n+1})\times \operatorname {Tor} H_{n}(L^{2n+1})\to \mathbb {Q} /\mathbb {Z} ,}$

представляющая собой важный топологический инвариант многообразия. В частности, инвариантом является совокупность всех коэффициентов самозацепления гомологических классов циклов размерности ${\displaystyle n}$ в многообразии размерности ${\displaystyle 2n+1}$^[23]. Например, в случае ${\displaystyle n=1}$ получается билинейная форма на подгруппе кручения первой группы гомологий замкнутого трёхмерного многообразия.

Комментарии

Источники

• Rolfsen, D.. Knots and Links (англ.). — AMS Chelsea Publishing, 2003. — 450 p. — ISBN 0-8218-3436-3.
• Duzhin, S. V., Chmutov, S. V., Mostovoy, J.. Introduction to Vassiliev Knot Invariants (рус.). — Cambridge University Press, 2012. — 512 с. — ISBN 978-1-107-02083-2. — doi:10.1017/CBO9781139107846.
• Болтянский, В. Г., Ефремович, В. А. Наглядная топология (англ.). — М.: Наука (издательство), 1982. — Vol. 21. — 160 p. — (Библиотечка «Квант»).
• Мантуров, В. О.. Теория узлов (рус.). — Москва-Ижевск: Институт компьютерных исследований, 2005. — 512 с. — ISBN 5-93972-404-3.
• Зейферт, Г., Трельфалль, В.. Топология (рус.). — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — 448 с. — ISBN 5-93972-068-4. Архивировано 7 декабря 2008 года.

• Gauss, C. F. Zur Mathematischen Theorie der electrodynamischen Wirkungen (нем.) // Werke. — Königlichen Gesllschaft der Wissenschaften zu Göttingen, 1877. — Bd. 5. — S. 601—630. — doi:10.1007/978-3-642-49319-5_42.
• Ricca, R. L., Nipoti, B.. Gauss' linking number revisited (англ.) // Journal of Knot Theory and Its Ramifications. — World Scientific Publishing Company, 2011. — Vol. 20, no. 10. — P. 1325—1343. — doi:10.1142/S0218216511009261.
• Meilhan, J.-B.. Linking number and Milnor invariants (англ.). — 2018. — arXiv:1812.03319v1.