Евклид

Евклид
др.-греч. Εὐκλείδης
Статуя в честь Евклида в Музее естественной истории Оксфордского университета.
Имя при рождении	др.-греч. Εὐκλείδης[1]
Дата рождения	около 325 года до н. э.
Место рождения	неизвестно[2]
Дата смерти	около 265 года до н. э.
Место смерти	Александрия, Эллинистический Египет
Страна	Древние Афины
Род деятельности	математик, писатель
Научная сфера	математика
Ученики	Diocleides of Athens[вд][3]
Известен как	«Отец Геометрии»
Цитаты в Викицитатнике
Произведения в Викитеке
Медиафайлы на Викискладе

Евкли́д (или Эвкли́д, др.-греч. Εὐκλείδης, от «добрая слава»^[4]; жил примерно в период 325 — 265 годы до н. э.^[5]) — древнегреческий математик, геометр, автор первого из дошедших до нас теоретических трактатов по математике. Биографические сведения о Евклиде крайне скудны. Достоверным можно считать лишь то, что его научная деятельность протекала в Александрии в III веке до н. э.^[6]

Евклид — первый математик Александрийской школы. Его главная работа «Начала» (Στοιχεῖα, в латинизированной форме — «Элементы») содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел; в ней он подвёл итог предшествующему развитию древнегреческой математики и создал фундамент дальнейшего развития данной науки. Другие его сочинения: «О делении фигур», сохранившееся в арабском переводе, 4 книги «Конические сечения», материал которых вошёл в одноимённое произведение Аполлония Пергского, а также «Поризмы», представление о которых можно получить из «Математического собрания» Паппа Александрийского. Евклид также автор работ по астрономии, оптике, музыке и др.^[7]

К наиболее достоверным сведениям о жизни Евклида принято относить то немногое, что приводится в комментариях Прокла к первой книге Начал Евклида (хотя следует принять во внимание, что Прокл жил спустя почти 800 лет после Евклида). Отметив, что «писавшие по истории математики» не довели изложение развития этой науки до времени Евклида, Прокл указывает, что Евклид был моложе Платоновского кружка, но старше Архимеда и Эратосфена, «жил во времена Птолемея I Сотера», «потому что и Архимед, живший при Птолемее Первом, упоминает об Евклиде и, в частности, рассказывает, что Птолемей спросил его, есть ли более короткий путь изучения геометрии, нежели Начала; а тот ответил, что нет царского пути к геометрии»^[8][9].

Дополнительные штрихи к портрету Евклида можно почерпнуть у Паппа и Стобея. Папп сообщает, что Евклид был мягок и любезен со всеми, кто мог хотя бы в малейшей степени способствовать развитию математических наук, а Стобей передаёт ещё один анекдот о Евклиде. Приступив к изучению геометрии и разобрав первую теорему, один юноша спросил у Евклида: «А какая мне будет выгода от этой науки?» Евклид подозвал раба и сказал: «Дай ему три обола, раз он хочет извлекать прибыль из учёбы»^[10]. Историчность рассказа сомнительна, поскольку аналогичный рассказывают о Платоне.

Некоторые современные авторы трактуют утверждение Прокла — Евклид жил во времена Птолемея I Сотера — в том смысле, что Евклид жил при дворе Птолемея и был основателем Александрийского Мусейона^[11]. Это представление утвердилось в Европе в XVII веке, средневековые же авторы отождествляли Евклида с учеником Сократа философом Евклидом из Мегар.

Арабские авторы считали, что Евклид жил в Дамаске и издал там «Начала» Аполлония.^[12] Анонимная арабская рукопись XII века сообщает :

Евклид, сын Наукрата, известный под именем «Геометра», учёный старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира…

С именем Евклида также связывают становление александрийской математики (геометрической алгебры), как науки^[13]. В целом количество данных о Евклиде настолько скудно, что существует версия (правда, малораспространённая) что речь идёт о коллективном псевдониме группы александрийских учёных^[14].

Основное сочинение Евклида называется Начала. Книги с таким же названием, в которых последовательно излагались все основные факты геометрии и теоретической арифметики, составлялись ранее Гиппократом Хиосским, Леонтом и Февдием. Однако Начала Евклида вытеснили все эти сочинения из обихода и в течение более чем двух тысячелетий оставались базовым учебником геометрии. Создавая свой учебник, Евклид включил в него многое из того, что было создано его предшественниками, обработав этот материал и сведя его воедино.

Начала состоят из тринадцати книг. Первая и некоторые другие книги предваряются списком определений. Первой книге предпослан также список постулатов и аксиом. Как правило, постулаты задают базовые построения (напр., «требуется, чтобы через любые две точки можно было провести прямую»), а аксиомы — общие правила вывода при оперировании с величинами (напр., «если две величины равны третьей, они равны между собой»).

В I книге изучаются свойства треугольников и параллелограммов; эту книгу венчает знаменитая теорема Пифагора для прямоугольных треугольников. Книга II, восходящая к пифагорейцам, посвящена так называемой «геометрической алгебре». В III и IV книгах излагается геометрия окружностей, а также вписанных и описанных многоугольников; при работе над этими книгами Евклид мог воспользоваться сочинениями Гиппократа Хиосского. В V книге вводится общая теория пропорций, построенная Евдоксом Книдским, а в VI книге она прилагается к теории подобных фигур. VII—IX книги посвящены теории чисел и восходят к пифагорейцам; автором VIII книги, возможно, был Архит Тарентский. В этих книгах рассматриваются теоремы о пропорциях и геометрических прогрессиях, вводится метод для нахождения наибольшего общего делителя двух чисел (известный ныне как алгоритм Евклида), строятся чётные совершенные числа, доказывается бесконечность множества простых чисел. В X книге, представляющей собой самую объёмную и сложную часть Начал, строится классификация иррациональностей; возможно, что её автором является Теэтет Афинский. XI книга содержит основы стереометрии. В XII книге с помощью метода исчерпывания доказываются теоремы об отношениях площадей кругов, а также объёмов пирамид и конусов; автором этой книги по общему признанию является Евдокс Книдский. Наконец, XIII книга посвящена построению пяти правильных многогранников; считается, что часть построений была разработана Теэтетом Афинским.

В дошедших до нас рукописях к этим тринадцати книгам прибавлены ещё две. XIV книга принадлежит александрийцу Гипсиклу (ок. 200 г. до н. э.), а XV книга создана во время жизни Исидора Милетского, строителя храма св. Софии в Константинополе (начало VI в. н. э.).

Начала предоставляют общую основу для последующих геометрических трактатов Архимеда, Аполлония и других античных авторов; доказанные в них предложения считаются общеизвестными. Комментарии к Началам в античности составляли Герон, Порфирий, Папп, Прокл, Симпликий. Сохранился комментарий Прокла к I книге, а также комментарий Паппа к X книге (в арабском переводе). От античных авторов комментаторская традиция переходит к арабам, а потом и в Средневековую Европу.

В создании и развитии науки Нового времени Начала также сыграли важную идейную роль. Они оставались образцом математического трактата, строго и систематически излагающего основные положения той или иной математической науки.

Из других сочинений Евклида сохранились:

• Данные (δεδομένα) — о том, что необходимо, чтобы задать фигуру;
• О делении (περὶ διαιρέσεων) — сохранилось частично и только в арабском переводе; даёт деление геометрических фигур на части, равные или состоящие между собой в заданном отношении;
• Явления (φαινόμενα) — приложения сферической геометрии к астрономии;
• Оптика (ὀπτικά) — о прямолинейном распространении света.

По кратким описаниям известны:

• Поризмы (πορίσματα) — об условиях, определяющих кривые;
• Конические сечения (κωνικά);
• Поверхностные места (τόποι πρὸς ἐπιφανείᾳ) — о свойствах конических сечений;
• Псевдария (ψευδαρία) — об ошибках в геометрических доказательствах (математические софизмы);

Евклиду приписываются также:

• Катоптрика (κατοπτρικά) — теория зеркал; сохранилась обработка Теона Александрийского;
• Деление канона (κατατομὴ κανόνος) — трактат по элементарной теории музыки^[15].

Уже со времён пифагорейцев и Платона арифметика, музыка, геометрия и астрономия (так называемые «математические» науки; позже Боэцием названные квадривием) рассматривались в качестве образца систематического мышления и предварительной ступени для изучения философии. Не случайно возникло предание, согласно которому над входом в платоновскую Академию была помещена надпись «Да не войдёт сюда не знающий геометрии».

Геометрические чертежи, на которых при проведении вспомогательных линий неявная истина становится очевидной, служат иллюстрацией для учения о припоминании, развитого Платоном в Меноне и других диалогах. Предложения геометрии потому и называются теоремами, что для постижения их истины требуется воспринимать чертёж не простым чувственным зрением, но «очами разума». Всякий же чертёж к теореме представляет собой идею: мы видим перед собой эту фигуру, а ведём рассуждения и делаем заключения сразу для всех фигур одного с ней вида.

Некоторый «платонизм» Евклида связан также с тем, что в Тимее Платона рассматривается учение о четырёх элементах, которым соответствуют четыре правильных многогранника (тетраэдр — огонь, октаэдр — воздух, икосаэдр — вода, куб — земля), пятый же многогранник, додекаэдр, «достался в удел фигуре вселенной». В связи с этим Начала могут рассматриваться как развёрнутое со всеми необходимыми посылками и связками учение о построении пяти правильных многогранников — так называемых «платоновых тел», завершающееся доказательством того факта, что других правильных тел, кроме этих пяти, не существует.

Для аристотелевского учения о доказательстве, развитого во Второй аналитике, Начала также предоставляют богатый материал. Геометрия в Началах строится как выводная система знаний, в которой все предложения последовательно выводятся одно за другим по цепочке, опирающейся на небольшой набор начальных утверждений, принятых без доказательства. Согласно Аристотелю, такие начальные утверждения должны иметься, так как цепочка вывода должна где-то начинаться, чтобы не быть бесконечной. Далее, Евклид старается доказывать утверждения общего характера, что тоже соответствует любимому примеру Аристотеля: «если всякому равнобедренному треугольнику присуще иметь углы, в сумме равные двум прямым, то это присуще ему не потому что он равнобедренный, а потому что он треугольник» (An. Post. 85b12).

Евклиду приписываются два важных трактата об античной теории музыки: «Гармоническое введение» («Гармоника») и «Деление канона» (лат. Sectio canonis). Традиция приписывать «Деление канона» Евклиду идёт ещё от Порфирия. В старинных рукописях «Гармоники» авторство приписывается Евклиду, некоему Клеониду, а также александрийскому математику Паппу. Генрих Мейбом (1555—1625) снабдил «Гармоническое введение» обстоятельными примечаниями, и вместе с «Делением канона» приписал их к трудам Евклида.

При последующем подробном анализе этих трактатов было определено, что первый написан в аристоксеновской традиции (например, в нём все полутоны считаются равными), а второй по стилю — явно пифагорейский (например, отрицается возможность деления тона ровно пополам). Стиль изложения «Гармонического введения» отличается догматизмом и непрерывностью, стиль «Деления канона» несколько схож с «Началами» Евклида, поскольку содержит теоремы и доказательства.

После критической публикации «Гармоники» знаменитым немецким филологом Карлом Яном (1836—1899) этот трактат стали повсеместно приписывать Клеониду и датировать II в. н. э. В русском переводе (с комментариями) его впервые издал Г. А. Иванов (Москва, 1894). «Деление канона» ныне одна часть исследователей считает аутентичным сочинением Евклида^[16], а другая — анонимным сочинением в традициях Евклида^[17]. Последние по времени русские переводы «Деления канона» опубликованы (в версии Порфирия) В. Г. Цыпиным и (в версии Боэция) С. Н. Лебедевым^[18]. Критическое издание оригинального текста «Деления канона» выполнил в 1991 г. А.Барбера^[19].

• Эвклидовы элементы из двенадцати нефтоновых книг выбранные и в осмь книг чрез профессора мафематики А. Фархварсона сокращённые. / Пер. с лат. И. Сатарова. СПб., 1739. 284 стр.
• Елементы геометрии, то есть первые основания науки о измерении протяжении, состоящие из осьми Евклидовых книг. / Пер. с франц. Н. Курганова. СПб., 1769. 288 стр.
• Евклидовых стихий осьмь книг, а именно: 1-я, 2-я, 3-я, 4-я, 5-я, 6-я, 11-я и 12-я. / Пер. с греч. СПб., 1784. 370 стр.
  • 2-е изд. … к сим прилагаются книги 13-я и 14-я. 1789. 424 стр.
• Эвклидовых начал восемь книг, а именно: первые шесть, 11-я и 12-я, содержащие в себе основания геометрии. / Пер. Ф. Петрушевского. СПб., 1819. 480 стр.
• Эвклидовых начал три книги, а именно: 7-я, 8-я и 9-я, содержащие общую теорию чисел древних геометров. / Пер. Ф. Петрушевского. СПб., 1835. 160 стр.
• Восемь книг геометрии Эвклида. / Пер. с нем. воспитанниками реального училища… Кременчуг, 1877. 172 стр.
• Начала Евклида. / С введ. и толкованиями М. Е. Ващенко-Захарченко. Киев, 1880. XVI, 749 стр.

• Армянский перевод Евклида
• 
  Армянский перевод Евклида (XIV), Матенадаран, MS. 8132
• 
• 
  Чертежи из армянской редакции XVII века «Начал» Евклида

В XI веке Григор Магистрос перевёл с греческого на армянский «Начала» Евклида. Более обширный перевод Евклида сделан в позднем средневековье и приписывается автору XVII века Григору Кесараци.

• Начала Евклида. Пер. и комм. Д. Д. Мордухай-Болтовского при ред. участии И. Н. Веселовского и М. Я. Выгодского. В 3 т. (Серия «Классики естествознания»). М.: ГТТИ, 1948-50. 6000 экз.

• Книги I—VI (1948. 456 стр.) на www.math.ru или на mccme.ru
• Книги VII—X (1949. 512 стр.) на www.math.ru или на mccme.ru
• Книги XI—XIV (1950. 332 стр.) на www.math.ru или на mccme.ru

• Оливер Бирн. Первые шесть книг Начал Евклида в которых используются цветные схемы и знаки вместо букв для большего удобства обучающихся / перевод с английского Сергея Слюсарева. — 2018. — 278 с.
• Евклидов корпус. Деление канона. Перевод А. Щетникова. ΣΧΟΛΗ, 6, 2012, c. 98-110.
• Евклид. Оптика. Перевод А. Щетникова. ΣΧΟΛΗ, 13, 2019, c. 771—822.
• Euclidus Opera Omnia. Ed. I. L. Heiberg & H. Menge. 9 vols. Leipzig: Teubner, 1883—1916.

• Vol. I—IX на www.wilbourhall.org

• Heath T. L. The thirteen books of Euclid’s Elements. 3 vols. Cambridge UP, 1925. Editions and translations: Greek (ed. J. L. Heiberg), English (ed. Th. L. Heath)
• Euclide. Les éléments. 4 vols. Trad. et comm. B. Vitrac; intr. M. Caveing. P.: Presses universitaires de France, 1990—2001.
• Barbera A. The Euclidian Division of the Canon: Greek and Latin Sources // Greek and Latin Music Theory. Vol. 8. Lincoln: University of Nebraska Press, 1991.

• Евклид : [арх. 3 декабря 2022] / Зубов А. Ю. // Динамика атмосферы — Железнодорожный узел. — М. : Большая российская энциклопедия, 2007. — С. 510. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 9). — ISBN 978-5-85270-339-2.
• Храмов Ю. А. Евклид // Физики : Биографический справочник / Под ред. А. И. Ахиезера. — Изд. 2-е, испр. и доп. — М. : Наука, 1983. — С. 109. — 400 с. — 200 000 экз.

• Max Steck. Bibliographia Euclideana. Die Geisteslinien der Tradition in den Editionen der «Elemente» des Euklid (um 365—300). Handschriften, Inkunabeln, Frühdrucke (16.Jahrhundert). Textkritische Editionen des 17.-20. Jahrhunderts. Editionen der Opera minora (16.-20.Jahrhundert). Nachdruck, herausgeg. von Menso Folkerts. Hildesheim: Gerstenberg, 1981.

• Прокл Диадох. Комментарии к первой книге «Начал» Евклида. Введение. Пер. и комм. Ю. А. Шичалина. М.: ГЛК, 1994.
• Прокл Диадох. Комментарий к первой книге «Начал» Евклида / Перевод А. И. Щетникова. — М.: Русский фонд содействия образованию и науке, 2013.
• Thompson W. Pappus’ commentary on Euclid’s Elements. Cambridge, 1930.

О Началах Евклида:

• Алимов Н. Г. Величина и отношение у Евклида // Историко-математические исследования. Вып. 8. — 1955. — С. 573—619.
• Башмакова И. Г. Арифметические книги «Начал» Евклида // Историко-математические исследования. Вып. 1. — 1948. — С. 296—328.
• Ван дер Варден Б. Л. Пробуждающаяся наука. — М.: Физматгиз, 1959.
• Выгодский М. Я. «Начала» Евклида // Историко-математические исследования. Вып. 1. — 1948. С. 217—295.
• Глебкин В. В. Наука в контексте культуры: («Начала» Евклида и «Цзю чжан суань шу»). — М.: Интерпракс, 1994. — 188 с. — 3000 экз. — ISBN 5-85235-097-4
• Евклид, его продолжатели и комментаторы // Каган В. Ф. Основания геометрии. Ч. 1. — М., 1949. — С. 28-110.
• Раик А. Е. Десятая книга «Начал» Евклида // Историко-математические исследования. Вып. 1. — 1948. — С. 343—384.
• Родин А. В. Математика Евклида в свете философии Платона и Аристотеля. — М.: Наука, 2003.
• Цейтен Г. Г. История математики в древности и в средние века. — М.-Л.: ОНТИ, 1938.
• Щетников А. И. Вторая книга «Начал» Евклида: её математическое содержание и структура // Историко-математические исследования. Вып. 12 (47). — 2007. — С. 166—187.
• Щетников А. И. Сочинения Платона и Аристотеля как свидетельства о становлении системы математических определений и аксиом. ΣΧΟΛΗ. Вып. 1. — 2007. — С. 172—194.
• Artmann B. Euclid’s «Elements» and its prehistory. Apeiron, v. 24, 1991, p. 1-47.
• Brooker M.I.H., Connors J. R., Slee A. V. Euclid. CD-ROM. Melbourne, CSIRO-Publ., 1997.
• Burton H.E. The optics of Euclid. J. Opt. Soc. Amer., v. 35, 1945, p. 357—372.
• Itard J. Lex livres arithmetiqués d’Euclide. P.: Hermann, 1961.
• Fowler D.H. An invitation to read Book X of Euclid’s Elements. Historia Mathematica, v. 19, 1992, p. 233—265.
• Knorr W.R. The evolution of the Euclidean Elements. Dordrecht: Reidel, 1975.
• Mueller I. Philosophy of mathematics and deductive structure in Euclid’s Elements. Cambridge (Mass.), MIT Press, 1981.
• Schreiber P. Euklid. Leipzig: Teubner, 1987.
• Seidenberg A. Did Euclid’s Elements, Book I, develop geometry axiomatically? Archive for History of Exact Sciences, v. 14, 1975, p. 263—295.
• Staal J.F. Euclid and Panini // Philosophy East and West.1965.№ 15. P. 99-115.
• Taisbak C.M. Division and logos. A theory of equivalent couples and sets of integers, propounded by Euclid in the arithmetical books of the Elements. Odense UP, 1982.
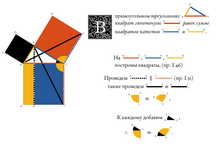
• Taisbak C.M. Colored quadrangles. A guide to the tenth book of Euclid’s Elements. Copenhagen, Museum Tusculanum Press, 1982.
• Tannery P. La géometrié grecque. Paris: Gauthier-Villars, 1887.

О других сочинениях Евклида:

• Зверкина Г. А. Обзор трактата Евклида «Данные» // Математика и практика, математика и культура. — М., 2000. — С. 174—192.
• Ильина Е. А. О «Данных» Евклида // Историко-математические исследования. Вып. 7 (42). — 2002. — С. 201—208.
• Шаль М. О поризмах Евклида // Исторический обзор происхождения и развития геометрических методов. — М., 1883.
• Berggren J.L., Thomas R.S.D. Euclid’s Phaenomena: a translation and study of a Hellenistic treatise in spherical astronomy. NY, Garland, 1996.
• Schmidt R. Euclid’s Recipients, commonly called the Data. Golden Hind Press, 1988.
• С. Кутателадзе Апология Евклида