Побудова за допомогою циркуля та лінійки

Ця стаття містить правописні, лексичні, граматичні, стилістичні або інші мовні помилки, які треба виправити. Ви можете допомогти вдосконалити цю статтю, погодивши її із чинними мовними стандартами.

Побудова за допомогою циркуля та лінійки або класична побудова, це побудова довжин, кутів, та інших геометричних фігур з використанням лише ідеалізованої лінійки та циркуля.

Ідеалізована лінійка, відома як прямий край^[en], вважається нескінченною, не має міток і має лише один край. Вважається, що циркуль відривається від креслення, тому не може бути безпосередньо використаний для перенесення відстаней. Це несуттєве обмеження, оскільки використовуючи процедуру з великою кількістю кроків, відстань може бути знайдена навіть за умови, що циркуль піднімають над кресленням; див. теорему еквівалентності циркулів^[en]. Формально кажучи, єдиними дозволеними конструкціями є такі, що надані трьома першими евклідовими постулатами.

Відомо, що будь-яка побудова з використанням лінійки та циркуля може бути виконана лише циркулем.

Математики стародавньої Греції вперше запровадили побудови за допомогою циркуля та лінійки, та ряд проблем у геометрії Евкліда накладають це обмеження. Стародавні греки розвинули багато побудов, хоча у деяких випадках не мали на це змоги. Гаусс продемонстрував, що деякі многокутники можна побудувати, але не всі. Принципова неможливість побудови, щодо деяких найвідоміших проблем, були доведені П'єром Ванцелем в 1837 році, за допомогою математичної теорії полів.

Не зважаючи на наявні докази неможливості побудови, знаходяться люди, що завзято намагаються вирішити ці питання.^[1] Більшість з цих питань легко вирішити за умови, що інші геометричні перетворення допускаються: наприклад, подвоєння куба можна зробити за допомогою геометричних побудов, але це не можливо, якщо використовувати лише лінійку і циркуль.

З точки зору алгебри, довжина може бути побудована тоді й лише тоді, коли є числом, що можна побудувати, та кут можна побудувати лише за умови того, що його косинус — це число, яке можна побудувати. Число може бути побудоване тоді й лише тоді, якщо його можна записати з використанням чотирьох базових арифметичних операції та лише квадратного кореня, але не кореня іншого степеня.

«Циркуль» та «лінійка», які використовуються для побудови — це ідеалізація реальних лінійки та циркуля. Тому припускається, що:

• Циркуль може бути розгорнутим на довільну ширину, але (на відміну від деяких існуючих циркулів) на ньому нема розмітки. Кола можуть бути накреслені лише за двома заданими точками: центром та точкою на колі. Циркуль може (не обов'язково) зникати, коли він не малює коло.
• Лінійка нескінченно довга, але не має відміток, бо у неї є лише прямий край, на відміну від звичайних лінійок. Вона може бути використана лише для креслення відрізків між двома точками або для подовження наявних відрізків.

Сучасні циркулі зазвичай не збиваються, і деякі сучасні побудови використовують цю особливість. Здавалося б, що сучасний циркуль — це «більш потужний» інструмент аніж стародавні циркулі, що збиваються. Однак, за 2 Теоремою з 1 Книги Початків Евкліда, ефективність при використанні циркуля, що збивається, не втрачається. Хоча теорема правдива, її докази мають довгу, та мінливу історію.^[2]

Кожна побудова повинна бути точною. Наближене рішення (або використання деяких інструментів виміру, таких як поділки на лінійці) не враховується за розв'язок.

Кожна побудова має мати завершення. Тобто вона повинна складатись зі скінченної кількості кроків, і не може бути межею послідовних наближень.

Побудови за допомогою циркуля та лінійки скоріше виникли як салонна гра^[en], а не справжня, практична задача; але метою наведених обмежень є гарантія того, що така побудова може бути виконана цілковито правильно, і це важливо як для виконання креслень (при проектуванні у програмах САПР та традиційних креслень олівцем, циркулем та лінійкою на папері) так і науці мір та вагів, у яких точна передача з об'єктів або матеріалів дуже важлива. Однією з головних цілей грецької математики було знаходження точної побудови для різних довжин; наприклад, знаходження сторони п'ятикутника вписаного у коло. Також, серед побудов, які греки не могли віднайти побудову, найбільш відомі наступні три випадки:

• Квадратура круга: Креслення квадрата з тією ж площею, що і дане коло.
• Подвоєння куба: Креслення куба з об'ємом, який буде вдвічі більший за об'єм даного куба.
• Трисекція кута: Поділ даного кута на три менші кути однакової градусної міри.

Протягом 2000 років люди намагались віднайти побудову за наведених умов, але їх зусилля не принесли потрібного результату. Наразі доведена неможливість розв'язання цих трьох проблем за математичними правилами (кути з деякими градусними мірами можуть бути поділені на три рівні частині, але не будь-який довільний кут).

Математики стародавньої Греції вперше використали побудову за допомогою лінійки та циркуля, та відкрили як будувати суму, різницю, добуток, відношення та квадратний корінь даних довжин.^{[3]:p. 1} Також вони могли конструювати половину даного кута, квадрат чиєї площі вдвічі більший за інший квадрат, квадрат, що має площу таку ж як даний багатокутник, та правильний багатокутник із трьома, чотирма або п'ятьма сторонами^{[3]:p. xi} (або такий, що має удвічі більше сторін ніж даний багатокутник^{[3]:pp. 49–50}). Але вони не могли побудувати третину кута, за виключенням окремих випадків, або квадрат із такою ж площею, що і дане коло, або правильний багатокутник з іншою кількістю сторін.^{[3]:p. xi} Не могли вони, також, побудувати грань куба, чий об'єм був удвічі більший за об'єм куба з даною гранню.^{[3]:p. 29}

Гіппократ та Менехм показали, що поверхня куба може бути подвоєна шляхом знаходження перетинів гіпербол та парабол, але вони не можуть бути побудовані циркулем та лінійкою.^{[3]:p. 30} У п'ятому столітті до нашої ери, Гіппократ використовував криву що він називав квадратриса як для розділення на три загального кута та квадратури круга, а Нікомед у другому столітті до нашої ери показав, як використовувати конхоїду для поділу довільного кута на три;^{[3]:p. 37} але ці методи також не можуть бути використані лише з циркулем та лінійкою.

Не було ніякого прогресу у вирішенні цих питань протягом двох тисячоліть, аж до 1796 року, поки Гаус показав, як побудувати правильний багатокутник з 17 сторонами; через п'ять років він навів достатні умови побудови правильного багатокутника з n сторонами.^{[3]:pp. 51 ff.}

У 1837 П'єр Ванцель опублікував доказ неможливості поділу на три частини довільного кута або подвоєння об'єму куба, Це доведення засноване на неможливості побудови кубічних коренів від довжин.^[4] Ще він показав, що достатні умови Гауса для побудови правильних багатокутників також є і необхідними.

Потім у 1882 році Ліндеманн показав, що ${\displaystyle \pi }$ це трансцендентне число, а отже не можливо побудувати за допомогою лінійки та циркуля квадрат із такою ж площею, що і дане коло.^{[3]:p. 47}

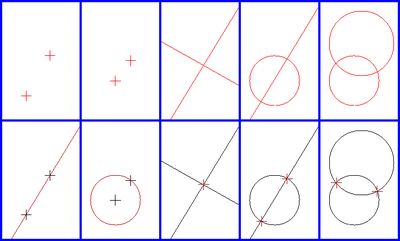
Усі побудови за допомогою лінійки та циркуля складаються з повторюваних додавань п'яти базових конструкцій, що використовують точки, лінії та кола, які вже були побудовані раніше. А саме:

• Побудова прямої, що проходить через дві задані точки
• Побудова кола з заданим центром, що проходить через задану точку
• Побудова точки, що є точкою перетину двох заданих, не паралельних ліній.
• Побудова однієї чи двох точок перетину кола з прямою лінією (якщо вони перетинаються)
• Побудова однієї чи двох точок на перетині двох кіл (якщо вони перетинаються).

Наприклад, для двох заданих різних точок ми можемо побудувати пряму або будь-яке з двох кіл (послідовно, використовуючи кожну точку як центр, а іншу точку, як точку на колі). Якщо накреслити обидва кола, то дві нові точки будуть утворені на перетині кіл. Креслення ліній між двома початковими точками та однією з цих нових точок завершує побудову рівностороннього трикутнику.

Таким чином, у будь-якій геометричній задачі на побудову задано початковий набір символів (точок та ліній), алгоритм дій, та певні результати. З цієї точки зору, геометрія еквівалентна до аксіоматичної алгебри, з точністю до заміни елементів на символи. Ймовірно, Гаус перший зрозумів це, та використав це для доказу неможливості деяких побудов; і лише через значний проміжок часу Гільберт винайшов повну систему геометричних аксіом.

Існують такі побудови за допомогою лінійки та циркуля, що застосовуються найчастіше:

• Побудова серединного перпендикуляра для відрізка
• Знаходження середньої точки (див. приклад нижче)
• Креслення прямої, що проходить через задану точку та перпендикулярна заданій прямій
• Бісекція кута
• Відбиття точки відносно прямої
• Побудова прямої, що проходить через точку та дотична до кола
• Побудова кола, яке проходить через три не колінеарні точки

Для прикладу розглянемо наступну задачу.

Задача. За допомогою циркуля та лінійки поділити даний відрізок AB на дві рівні частини. Один з розв'язків показано на малюнку. Розв'язок складається з наступних кроків:

• Циркулем будуємо коло з центром в точці A радіусу AB.
• Будуємо коло з центром в точці B радіусу AB.
• Знаходимо точки перетину P та Q двох побудованих кіл.
• Лінійкою проводимо відрізок, що об'єднує точки P та Q.
• Знаходимо точку перетину AB та PQ. Це — шукана середина відрізка AB.

Існують багато різних методів доказу неможливості чого-небудь. Якомога ретельніше доведення потрібне для визначення межі можливого, та щоб показати те, що для вирішення проблеми ми повинні переступити цю межу. Більша частина того, що можливо побудувати визначається теоремою про пропорційні відрізки.

Ми можемо асоціювати алгебру із нашою геометрією використовуючи Декартову систему координат, утворену двома лініями, та представляють точки площині як вектори. Остаточно, ми можемо записати ці вектори як комплексні числа.

Використовуючи рівняння для ліній та кіл, можна показати, що точки їх перетину лежать у квадратичному розширенні^[en] найменшого поля F, що містить дві точки на лінії, центр кола та радіус кола. Тобто вони утворюють числа вигляду ${\displaystyle x+y{\sqrt {k}}}$, де x, y, та k лежать у F.

Оскільки поле точок, що можна побудувати замкнене відносно квадратних коренів, воно містить усі точки, які можна отримати скінченною послідовністю квадратичних розширень поля комплексних точок їх раціональними коефіцієнтами. Згідно з попереднім абзацом, можна показати, що будь-яка точка може бути отримана такою послідовністю розширень. Як наслідок цього, можна сказати, що мінімальний поліном для точки, що доступна до побудови (і через це будь-яка довжина, яку можна побудувати), має степінь 2. Зокрема будь-яка конструктивна точка (або довжина) це алгебраїчне число, однак не кожне алгебраїчне число є конструктивним (так зв'язок між конструктивною довжиною та алгебраїчним числом не є бієктивним); наприклад, ${\displaystyle {\sqrt[{3}]{2}}}$ алгебраїчне, але не конструктивне число.

Існує бієктивний зв'язок між кутами, які можна побудувати та точками, що конструктивні на будь-якому конструктивному колі. Конструктивні кути утворюють абелеву групу з модулем додавання ${\displaystyle 2\pi }$ (що відповідає множенню точок на одиничному колі, як комплексних чисел). Кути, що можна побудувати — це саме ті кути, тангенс яких (або так-само, синус чи косинус) є конструктивним як число. Наприклад, правильний сімнадцятикутник є конструктивним, бо

${\displaystyle \cos {\left({\frac {2\pi }{17}}\right)}=-{\frac {1}{16}}\;+\;{\frac {1}{16}}{\sqrt {17}}\;+\;{\frac {1}{16}}{\sqrt {34-2{\sqrt {17}}}}\;+\;{\frac {1}{8}}{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}}}$

що віднайшов Гаус.^[5]

Група конструктивних кутів замкнена відносно операції ділення кутів навпіл (що відповідає взяттю квадратного кореня з комплексних чисел). Єдиними кутами фінітного порядку що можуть бути побудованими починаючи з двох точок є ті, чий порядок є або степенем двійки, або добутком степені двійки та множини різних чисел Ферма. Слід зауважити, що існує нескінченна щільна множина конструктивних кутів.

Дано множину точок в Евклідовому просторі, обираємо одну з них за 0 та іншу за 1, разом з довільним вибором орієнтації дозволить нам розглядати ці точки як множину комплексних чисел.

Якщо брати будь-яку таку інтерпретацію множини точок у ролі комплексних чисел, точки, які можна побудувати за допомогою лінійки та циркуля, є в точності елементами найменшого поля, що містить початкову множину точок та замкнене відносно операцій над спряження та видобутку квадратного кореня (щоб уникнути двозначності, варто вважати, що квадратний корінь береться з комплексним аргументом^[en] меншим за ${\displaystyle \pi }$). Елементи цього поля це в точності ті, що можуть бути виражені як формула у початкових точках, яка використовує лише операції додавання, віднімання, множення, ділення, знаходження спряженого числа, та квадратний корінь, для яких легко побачити, що вони є зліченною підмножиною площини. Кожна з шести операцій відповідає простим побудовам за допомогою циркуля та лінійки. З такого твердження є очевидною побудова відповідної точки комбінуванням конструкцій кожної з арифметичних операцій. Більш ефективні побудови окремої множини точок відповідає скороченню у таких обчисленнях.

Так само (та без необхідності довільного вибору двох точок) ми можемо сказати, що за умови довільного вибору орієнтації, множина точок визначає множину комплексних коефіцієнтів відношенням різності між будь-якими двома парами точок. Множина коефіцієнтів конструктивна при використанні циркуля та лінійки, з такого набору коефіцієнтів, найменше поле містить початкові коефіцієнти та замкнене щодо знаходження спряженого числа та взяття квадратного кореня.

Наприклад, дійсна частина, уявна частина та модуль точки або коефіцієнта z (якщо брати одну з двох точок, що розглядались вище) конструктивні оскільки вони можуть бути записані як

${\displaystyle \mathrm {Re} (z)={\frac {z+{\bar {z}}}{2}}\;}$

${\displaystyle \mathrm {Im} (z)={\frac {z-{\bar {z}}}{2i}}\;}$

${\displaystyle \left|z\right|={\sqrt {z{\bar {z}}}}.\;}$

Подвоєння куба та трисекція кута (за виключенням окремих кутів φ, таких, що φ/${\displaystyle 2\pi }$ є раціональне число зі знаменником, що не ділиться на 3) потребує коефіцієнтів, що є розв'язками кубічних рівнянь, у той час, коли квадратура круга потребує трансцендентного коефіцієнта. Жодна з цих операцій не належить полям, описаним вище, отже побудови за допомогою лінійки та циркуля для них не існує.

Стародавні греки вважали, що проблеми побудови, які вони не могли вирішити були просто важкими для розв'язання, але не такими, що їх неможливо побудувати.^[6] З допомогою сучасних методів була доведена логічна неможливість виконання цих побудов за допомогою лінійки та циркуля. (Самі проблеми, однак, мають рішення, і греки знали як їх розв'язати, без обмеження у використанні лише лінійки та циркуля.)

Найвідоміша з цих проблем — квадратура круга, включає побудову квадрата з такою ж площею, як і даний круг з використанням лише лінійки та циркуля.

Неможливість квадратури круга була доведена завдяки тому, що вона включає в собі побудову трансцендентного числа, а саме числа ${\displaystyle {\sqrt {\pi }}}$. Тільки окремі алгебраїчні числа можуть бути побудовані лише лінійкою та циркулем, а саме ті, що побудовані з цілих чисел та скінченної послідовності операцій додавання, віднімання, множення, ділення, та взяття квадратного кореня. Через це фраза «квадратура круга» часто використовується у сенсі «робити щось неможливе».

Без обмеження на умову використання лише циркуля і лінійки, проблема легко вирішується за допомогою найрізноманітніших геометричних і алгебраїчних засобів, і багато разів була вирішена в античності.^[7]

За допомогою трикутника Кеплера можна отримати дуже близьке наближення до квадратури круга.

Подвоєння куба — це побудова, за умови використання лише лінійки та циркуля, грані куба, об'єм якого удвічі більший за об'єм куба з даною гранню. Це не можливо, оскільки корінь кубічний від двох, хоча б алгебраїчно, не може бути обчислений з цілих чисел за допомогою операцій додавання, віднімання, множення, ділення, та виділення квадратного кореня. З цього випливає, що його мінімальний многочлен з раціональними коефіцієнтами має степінь 3. Ця побудова можлива, якщо використовувати лінійку з двома відмітками на ній та на циркулі.

Трисекція кута — це побудова, з використанням тільки лінійки та циркуля, кута, що є третиною даного довільного кута. Це не можливо у загальному випадку. Наприклад, хоча кут ${\displaystyle \pi /3}$ радіан (60°) не може бути розділений на три рівних кути, кут ${\displaystyle 2\pi /5}$ радіан (72° = 360°/5) може бути поділений на три рівні частини. Головна проблемою трисекції може бути вирішена дуже легко, коли на лінійці є дві відмітки, що дають змогу використання невсіса.

Деякі правильні багатокутники такі як п'ятикутник легко будуються лінійкою та циркулем; інші — ні. Це наводить на питання: чи можливо побудувати усі правильні багатокутники лінійкою та циркулем?

У 1796 році Карл Фрідріх Гаус продемонстрував, що правильний 17 сторонній багатокутник може бути побудованим, та через 5 років показав, що правильний n-кутник може бути побудований лінійкою та циркулем, якщо непарні прості множники числа n будуть різними числами Ферма. Гаус висловив припущення, що ця умова буде не тільки достатньою, а й необхідною, але не зміг це довести, що було пізніше доведено П'єром Ванцелем у 1837 році.^[8]

Перші декілька конструктивних правильних многокутників мають таку кількість сторін:

3, 4, 5, 6, 8, 10, 12, 15, 16^[en], 17, 20^[en], 24^[en], 30^[en], 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272… послідовність A003401 з Онлайн енциклопедії послідовностей цілих чисел, OEIS

Відомо, що існує нескінченно багато конструктивних правильних багатокутників з парною кількістю сторін (тому, що раз можливо побудувати правильний n-кутник, то можна побудувати і правильний 2n-кутник, а отже і правильні 4-кутник, 8-кутник, тощо). Однак, відомо тільки 31 правильний n-кутник із непарною кількістю сторін, які можна побудувати.

У трикутника є шістнадцять ключових точок: вершини, середини його сторін, основи висот, основи бісектрис, а також його центр описаного кола, барицентр, ортоцентр, та центр вписаного кола. Вони можуть бути використані за потреби, для вирішення 139 різних нетривіальних задач побудови трикутника по трьом точкам.^[9] Серед цих проблем три потребують точку, яка може бути однозначно побудована з інших двох; 23 можуть бути не однозначно побудовані (насправді для нескінченної кількості розв'язків) але лише якщо на розташування точок накладено обмеження; у 74 ця проблема конструктивна для загального випадку; та у 39 шуканий трикутник існує, але його не можна побудувати.

Дванадцять ключових довжин трикутника: довжини сторін, висот, бісектрис та медіан. Разом з трьома кутами виникає 95 різних комбінацій, з яких 63 можна побудувати, 30 неможливо і 2 невизначені.^{[10]:pp. 201–203}

Відрізок з будь-якої точки на площині до найближчої точки на колі можна побудувати, але відрізок з будь-якої точки на площині до найближчої точки на еліпсі позитивного ексцентриситету взагалі не може бути побудований.^[11]

Стародавні греки класифікували конструкції на три основні категорії, в залежності від складності необхідних інструментів для їх вирішення. Якщо для побудови потрібні лише циркуль і лінійка, вона називалася плоскою; якщо потрібні конічні перетини (крім кола), то її називали міцною конструкцією; третя категорія включає всі конструкції, які не потрапили до жодної з двох категорій.^[12] Ця класифікація конструкцій красива з нашої сучасної алгебраїчної точки зору. Комплексне число, яке може бути виражено з використанням тільки операцій над полем і квадратних коренів (які описані вище) мають плоску конструкцію. Комплексне число, яке містить також видобуток кубічних коренів відповідає міцній конструкції.

Точка має міцну конструкцію, якщо вона може бути побудована з використанням лінійки, циркуля, і (можливо, гіпотетично) конічного інструменту для малювання, який може намалювати будь-який конічний малюнок з уже побудованим фокусом, директрисою та ексцентриситетом. Той же набір точок часто може бути побудований з використанням меншого набору інструментів. Наприклад, використовуючи циркуль, лінійку, і листок паперу, на якому ми маємо параболу ${\displaystyle y=x^{2}}$ разом з точками (0,0) і (1,0), можна побудувати будь-яке комплексне число, яке має міцну конструкцію, Крім того, інструмент, який може намалювати будь-який еліпс з уже побудованим фокусом і головною віссю (мається на увазі, що дві шпильки й шматок мотузки) є настільки ж потужними.^[13]

Стародавні греки знали, що подвоєння куба і трисекція довільного кута були міцними конструкціями. Архімед дав міцну конструкцію 7-кутника. Квадратура кола не має міцної конструкцію.

Регулярний ${\displaystyle n}$-кутник має міцну конструкцію, тоді і тільки тоді, коли ${\displaystyle n=2^{j}3^{k}m}$, де ${\displaystyle m}$ є добутком різних простих чисел Пірпонта^[en] (прості числа, які мають вигляд ${\displaystyle 2^{r}3^{s}+1}$). Множиною таких ${\displaystyle n}$ представлена послідовністю

7, 9, 13, 14, 18, 19, 21, 26, 27, 28, 35, 36, 37, 38, 39, 42, 45, 52, 54, 56, 57, 63, 65, 70, 72, 73, 74, 76, 78, 81, 84, 90, 91, 95, 97 … (послідовність A051913 в ЕПЦЧ)

Множина ${\displaystyle n}$, для яких правильний ${\displaystyle n}$-кутник не має міцної конструкції, є послідовністю

11, 22, 23, 25, 29, 31, 33, 41, 43, 44, 46, 47, 49, 50, 53, 55, 58, 59, 61, 62, 66, 67, 69, 71, 75, 77, 79, 82, 83, 86, 87, 88, 89, 92, 93, 94, 98, 99, 100 … (послідовність A048136 в ЕПЦЧ)

Подібно до питання з простими числами Ферма, залишається відкритим питання про те, чи існує нескінченно багато простих чисел Пірпонта.

За теоремою Мора — Маскероні за допомогою одного циркуля можна побудувати будь-яку фігуру, яку можна побудувати циркулем та лінійкою. При цьому пряма вважається побудованою, якщо на ній задано дві точки. Цілком можливо (відповідно до теореми Мора-Маскероні), щоб побудувати щось тільки з циркулем, за умови, що наведені дані, які повинні бути знайдені складаються з двох точок (а не ліній або кіл). Слід зазначити, що істинність цієї теореми залежить від істинності аксіоми Архімеда^[14], яка не є першого порядку в природі. Неможливо взяти квадратний корінь тільки з лінійкою, так що деякі речі, які не можуть бути побудовані за допомогою лінійки можна побудувати за допомогою циркуля; але (по теоремі Понселе - Штейнера^[en]) з урахуванням одного кола і його центра, то вони можуть бути побудовані.

Легко помітити, що за допомогою однієї лінійки можна реалізувати тільки проективно-інваріантні побудови. Зокрема, неможливо навіть розділити відрізок на дві рівні частини або знайти центр намальованого кола. Але за наявності на площині заздалегідь проведеного кола з позначеним центром за допомогою лінійки можна провести ті ж побудови, що і циркулем та лінійкою (теорема Понселе - Штейнера^[en]), 1833.

Математична теорія оригамі набагато потужніша ніж побудови циркулем та лінійкою. Складки, які задовільняють правила Худзити, можна побудувати з точно тим же набором точок, як міцну конструкцію з використанням циркуля, лінійки та конічного перетину. Тому, оригамі можна використати для розв'язку кубічних рівнянь (а з ними, і рівнянь четвертого степеня), що дозволяє вирішити дві з трьох класичних задач.^[15]

Архімед, Нікомед і Аполлоній описали побудови з використанням маркування лінійки. Це дозволило їм, наприклад, взяти відрізок, дві лінії (або кола), а також точку; а потім провести лінію, яка проходить через задану точку та перетинає обидві лінії, таким чином, що відстань між точками перетину дорівнює даному відрізку. Це греки називали neusis («схильність», «тенденція» або «межує»), так як нова лінія прагне до точки. У цій розширеній схемі, ми можемо ділити на три рівні частини довільний кут (див. трисекція Архімеда) або видобути довільний кубічний корінь (методом Нікомеда). Отже, будь-яка відстань, відношення якої до заданої відстані є рішенням кубічного або рівняння четвертого степеня, можна побудувати. Правильні багатокутники з міцними конструкціями, наприклад, семикутник, конструктивні; і Джон Х. Конвей і Річард К. Гай описали побудову деяких з них.^[16]

Побудова невсіс є більш потужною, ніж конічний інструмент для малювання, з її допомогою можна побудувати комплексні числа, які не мають міцних конструкцій. Насправді, за допомогою цього інструменту можна вирішити деякі рівняння високого степеня, які не можна розв'язати за допомогою радикалів.^[17] Відомо, що не можна розв'язати незвідний поліном з простою степеню, яка більше або дорівнює 7, з використанням невсіс побудови. Отже, не представляється можливим побудувати правильний 23-кутник або 29-кутник за допомогою цього інструменту. Бенджамін і Снайдер довели, що можна побудувати регулярний 11-кутник, але не надали способу побудови.^[18] Наразі залишається відкритим питання, щодо можливості побудови 25-ти та 31-кутника за допомогою цього інструмента.

У 1998 році Симон Плюффе^[en] дав алгоритм для циркуля і лінійки, який може використовуватися для обчислення двійкових символів певних чисел.^[19] Алгоритм включає в себе повторне подвоєння кута і стає фізично непрактичним після обчислення близько 20 двійкових символів.

• Задача Аполлонія
• Задача Брахмагупти
• GeoGebra
• Kig^[ru]
• KSEG^[ru] — програми для побудови за допомогою циркуля та лінійки^[20].
• Конструктивне число
• Цикл Карлейля^[en]
• Геометрична криптографія^[en]
• Геометрографія^[en]
• Список систем інтерактивної геометрії^[en] дозволяє користувачу будувати за допомогою циркуля та прямої лінії, а також маніпулювати побудовою, більшість з них демонструють побудови циркулем та лінійкою
• Underwood Dudley^[en] — математик, чиєю працею був збір невірних доведень за допомогою лінійки та циркуля.

• А. Адлер. Теорія геометричних побудов, [Архівовано 27 травня 2020 у Wayback Machine.] Переклад з німецької Г. М. Фіхтенгольца. Видання третє. Л., Навчпедвид, 1940—232 с.
• І. І. Алєксандров, Збірник геометричних задач на побудову, [Архівовано 7 грудня 2007 у Wayback Machine.] Видання вісімнадцяте, М., Навчпедвид, 1950—176 с.
• Б. І. Аргунов, М Б Балк. Геометричні побудови на площині, [Архівовано 18 грудня 2007 у Wayback Machine.] Посібник для студентів педагогічних інститутів. Видання друге. М., Навчпедвид, 1957—268 с.
• О. М. Воронець. Геометрія циркуля, [Архівовано 6 грудня 2007 у Wayback Machine.] Популярна бібліотека з математики під загальною редакцією Л. О. Люстерника, М.- Л., ОНТІ, 1934 — 40 с.
• В. О. Гейлер. Нерозв'язні задачі на побудову, СОЖ, 1999, No 12, с. 115—118.
• Ю. І.  Манін, Про розв'язність задач на побудову за допомогою циркуля та лінійки [Архівовано 18 жовтня 2009 у Wayback Machine.], Енциклопедія елементарної математики книга четверта (геометрія) [Архівовано 18 вересня 2011 у Wayback Machine.], М., Фізматвид, 1963. — 568с.
• Ю. Петерсен. Методи і теорії розв'язку геометричних задач на побудову, [Архівовано 7 грудня 2007 у Wayback Machine.] Москва, типографія Э.Ліснера та Ю.Романа, 1892 — VIII + 114с.
• В. В. Прасолов Три класичні задачі на побудову. Подвоєння куба, трисекція кута, квадратура круга, [Архівовано 28 грудня 2010 у Wayback Machine.] М.: Наука, 1992. 80 с. Серія Популярні лекції з математики, випуск 62
• Я. Штейнер, Геометричні побудови, виконувані за допомогою прямої лінії та нерухомого круга, [Архівовано 7 грудня 2007 у Wayback Machine.] М., Навчпедвид, 1939 — 80 с.
• Факультативний курс з математики. Микільська | 80
• Костарчук, В. М. Про можливе і неможливе в геометрії циркуля і лінійки / В. М. Костарчук, Б. І. Хацет. — К. : Радянська школа, 1971. — 128 с.

• Online ruler-and-compass construction tool [Архівовано 24 квітня 2016 у Wayback Machine.] (in French)
• Regular polygon constructions [Архівовано 12 квітня 2008 у Wayback Machine.] by Dr. Math at The Math Forum @ Drexel
• Construction with the Compass Only [Архівовано 14 травня 2008 у Wayback Machine.] at cut-the-knot
• Angle Trisection by Hippocrates [Архівовано 14 травня 2008 у Wayback Machine.] at cut-the-knot
• Weisstein, Eric W. Angle Trisection(англ.) на сайті Wolfram MathWorld.
• Various constructions using compass and straightedge [Архівовано 21 червня 2010 у Wayback Machine.] With interactive animated step-by-step instructions
• Math Tricks Help You Design Shop Projects: master a simple compass and you're a designer; convert your router into one with a trammel and away you go, Popular Science, May 1971, p104,106,108, Scanned article via Google Books: https://books.google.com/books?id=ngAAAAAAMBAJ&pg=PA104
• Visual Euclid [Архівовано 24 квітня 2016 у Wayback Machine.] slideshows of Euclidean constructions
• The Golden Ratio Determined Using a Ruler and Compass [Архівовано 22 квітня 2016 у Wayback Machine.] list of all the shortest constructions