Супереліпс

Супереліпс
Названо на честь	Габрієль Ламе
Формула	${\displaystyle \left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1}$
Підтримується Вікіпроєктом	Вікіпедія:Проєкт:Математика
Супереліпс у Вікісховищі

Супереліпс (крива Ламе) — плоска крива, що у декартових координатах описується рівнянням:

${\displaystyle \left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1,}$

де ${\displaystyle n>0}$;

${\displaystyle a}$ і ${\displaystyle b}$ — радіуси (півосі) супереліпса.

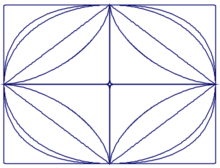
Для випадку n = 2 отримуємо еліпс (у частковому випадку, при a = b — коло), а при ${\displaystyle n=1}$ — ромб з діагоналями ${\displaystyle 2a}$ та ${\displaystyle 2b}$. Коли збільшувати ${\displaystyle n}$ до нескінченості, крива прямує за формою до прямокутника; натомість коли ${\displaystyle n}$ прямує до нуля, крива набуває хрестоподібної форми.

Фігури, що отримані для n < 2 ще називають «гіпоеліпс», а для n > 2 — «гіпереліпс».

Супереліпс може бути описаний парою рівнянь в параметричній формі:

${\displaystyle \left.{\begin{aligned}x\left(\theta \right)&=\pm a\cos ^{\frac {2}{n}}\theta \\y\left(\theta \right)&=\pm b\sin ^{\frac {2}{n}}\theta \end{aligned}}\right\}\qquad 0\leq \theta <{\frac {\pi }{2}}}$

або

${\displaystyle {\begin{aligned}x\left(\theta \right)&={|{\cos \theta }|}^{\frac {2}{n}}\cdot a\operatorname {sgn}(\cos \theta )\\y\left(\theta \right)&={|{\sin \theta }|}^{\frac {2}{n}}\cdot b\operatorname {sgn}(\sin \theta ).\end{aligned}}}$

Площа супереліпса виражається формулою

${\displaystyle S=4ab{\frac {\left(\Gamma \left(1+{\tfrac {1}{n}}\right)\right)^{2}}{\Gamma \left(1+{\tfrac {2}{n}}\right)}}.}$

Криві вперше були записані і вивчені французьким математиком Габрієлем Ламе, тому їх ще називають «криві Ламе».

Популяризацією цих кривих в архітектурі та при проектуванні предметів щоденного вжитку займався данський вчений, письменник, винахідник та інженер Піт Хейн (дан. Piet Hein; 1905—1996). У 1959 році архітектурне управління Стокгольма оголосило конкурс на проектування перехрестя з коловим рухом навколо площі Сергельсторг. Піт Хейн став переможцем конкурсу з пропозицією реалізувати транспортне кільце у вигляді супереліпса з n = 2,5 та a/b = 6/5^[1]. Реконструкцію площі було закінчено у 1967 році. Хейн використовував супереліпс в інших дизайнерських розробках — ліжках, тарілках, столах^[2]. При обертанні супереліпса навколо довгої осі, він отримав «суперяйце», яке стало популярною іграшкою за свою здатність на відміну від звичного яйця стояти вертикально на плоскій поверхні.

У 1968 році, коли делегації на переговорах в Парижі по війні у В'єтнамі не могли прийти до згоди щодо форми стола, було запропоновано стіл у вигляді супереліпса^[1]. Супереліптичну форму має стадіон «Ацтека» в Мехіко, головний стадіон Олімпійських ігор 1968 року.

На логотипі футбольної команди «Піттсбург Стілерс» зображені три чотирикутних зірки, що є супереліпсами з n = 0,5.

Супереліпс може розглядатись як частковий випадок суперформули, записаної у 1997 році бельгійським вченим Йоханом Джилісом (англ. Johan Gielis). Тривимірним відповідником супереліпса є суперквадрікс^[en] (англ. Superquadrics). В частковому випадку, коли a = b = 1 та n парне ціле число, супереліпс є кривою Ферма степеня n.

• Астроїда — супереліпс з n = 2/3 і a = b, гіпоциклоїда з чотирма кутами.
  • Дельтоїда — трикутна гіпоциклоїда.
• Сквиркл — супереліпс n = 4 і a = b, що виглядає як «чотирикутне колесо».
  • Трикутник Рело — «трикутне колесо».

• Супереліпс [Архівовано 21 січня 2012 у Wayback Machine.] (англ.) в енциклопедії MathWorld