凱萊圖

凱萊圖（英語：Cayley graph），也叫做凱萊著色圖，是將離散群的抽象結構畫出的一種圖。它的定義是凱萊定理（以阿瑟·凱萊命名）所暗含的。畫凱萊圖時，要選定群的一個生成元集合（通常有限），不同選法可能得到不同的凱萊圖。凱萊圖是組合群論（英语：Combinatorial group theory）與幾何群論的中心工具。

假設${\displaystyle G}$是群，而${\displaystyle S}$是G的生成集。凱萊圖${\displaystyle \Gamma =\Gamma (G,S)}$，是如下構造的著色的有向圖：

• ${\displaystyle G}$的每個元素${\displaystyle g}$對應一個頂點。換言之，圖${\displaystyle \Gamma }$的頂點集合${\displaystyle V(\Gamma )}$視為與${\displaystyle G}$等同；
• ${\displaystyle S}$中每個生成元${\displaystyle s}$，對應一種顏色${\displaystyle c_{s}}$；
• 對於任何${\displaystyle g\in G,s\in S}$，畫一條由元素${\displaystyle g}$至${\displaystyle gs}$的有向邊，染成${\displaystyle c_{s}}$色。換言之，邊集合${\displaystyle E(\Gamma )}$由形如${\displaystyle (g,gs)}$的有序對構成，邊的顏色由${\displaystyle s\in S}$確定。

在幾何群論中，集合${\displaystyle S}$通常取為有限、對稱（即滿足${\displaystyle S=S^{-1}}$），并且不包含這個群的單位元${\displaystyle e}$。在這種情況下，凱萊圖是简单無向圖：它的邊沒有方向（由對稱性），并且不包含自環（因為${\displaystyle e\notin S}$）。

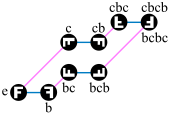
• 假設${\displaystyle G=\mathbb {Z} }$是無限循環群（即整數的加法群），而集合${\displaystyle S}$由標準生成元${\displaystyle 1}$和它的逆元（用加法符號為${\displaystyle -1}$）構成，則它的凱萊圖是無窮鏈（英语：Path graph）。
• 類似地，如果${\displaystyle G=\mathbb {Z} _{n}}$是${\displaystyle n}$階循環群（模${\displaystyle n}$的加法群），而${\displaystyle S}$仍由${\displaystyle G}$的標準生成元${\displaystyle 1}$與逆元${\displaystyle -1}$構成，則凱萊圖是環圖${\displaystyle C_{n}}$。
• 群的直積的凱萊圖（新生成集取為原生成集之笛卡爾積），是對應的凱萊圖的笛卡爾積（英语：Cartesian product of graphs）。因此阿貝爾群${\displaystyle \mathbb {Z} ^{2}}$，關於四個元素${\displaystyle (\pm 1,\pm 1)}$組成的生成集的凱萊圖，是平面${\displaystyle \mathbb {R} ^{2}}$上的無窮網格，而帶有類似的生成集的直積${\displaystyle \mathbb {Z} _{n}\times \mathbb {Z} _{m}}$的凱萊圖，是環面上的${\displaystyle n}$乘${\displaystyle m}$有限網格。
• 二面體群${\displaystyle D_{4}}$有群展示：$${\displaystyle \langle a,b|a^{4}=b^{2}=e,ab=ba^{3}\rangle .}$$左圖是關於兩個生成元${\displaystyle a}$和${\displaystyle b}$的凱萊圖，其中紅色箭頭表示左乘元素${\displaystyle a}$（順時針旋轉${\displaystyle 90^{\circ }}$）。而因為元素${\displaystyle b}$（左右反射）自反，所以表示左乘元素${\displaystyle b}$的藍色線是無方向的，故左圖混合了有向邊與無向邊：它有${\displaystyle 8}$個頂點、${\displaystyle 8}$條有向邊、${\displaystyle 4}$條無向邊。

  

  

  同一個群${\displaystyle D_{4}}$，亦可畫出不同的凱萊圖，如右圖。${\displaystyle b}$仍表示左右反射，而${\displaystyle c}$則是關於主對角線的反射，以粉紅色線表示。由於兩個反射皆自反，右邊的凱萊圖完全無向。對應的群展示是$${\displaystyle \langle b,c\mid b^{2}=c^{2}=e,bcbc=cbcb\rangle .}$$
• 條目開頭的圖，是兩個生成元${\displaystyle a,b}$上的自由群，關於生成集合${\displaystyle S=\{a,b,a^{-1},b^{-1}\}}$的凱萊圖，而正中央的黑點，是單位元${\displaystyle e}$。沿著邊向右走表示右乘${\displaystyle a}$，而沿著邊向上走表示乘以${\displaystyle b}$。因為自由群沒有關係，它的凱萊圖中沒有環。這個凱萊圖是證明巴拿赫-塔斯基悖论的關鍵。
• 右邊有離散海森堡群

  

$${\displaystyle \left\{{\begin{pmatrix}1&x&z\\0&1&y\\0&0&1\\\end{pmatrix}},\ x,y,z\in \mathbb {Z} \right\}}$$ 的凱萊圖。所用的三個生成元${\displaystyle X,Y,Z}$，分別對應${\displaystyle (x,y,z)=(1,0,0),\ (0,1,0),\ (0,0,1)}$。其關係為${\displaystyle Z=XYX^{-1}Y^{-1},\ XZ=ZX,\ YZ=ZY}$，亦可從圖中看出。本群為非交換無窮群。雖然是三維空間，其凱萊圖的增長（英语：Growth rate (group theory)）卻是${\displaystyle 4}$階的。^{[來源請求]}

群${\displaystyle G}$通過左乘作用在自身上（參見凱萊定理）。這個作用可以看作${\displaystyle G}$作用在它的凱萊圖上。明確而言，一個元素${\displaystyle h\in G}$映射一個頂點${\displaystyle g\in V(\Gamma )}$到另一個頂點${\displaystyle hg\in V(\Gamma )}$。凱萊圖的邊集合被這個作用所保存：邊${\displaystyle (g,gs)}$變換成邊${\displaystyle (hg,hgs)}$。任何群在自身上的左乘作用是簡單傳遞的，特別是凱萊圖是頂點傳遞（英语：Vertex-transitive graph）的。事實上，反向的結論也成立，即有下列等價刻劃，稱為扎比杜西定理（英語：Sabidussi's Theorem）：

（無標記又無着色）有向圖${\displaystyle \Gamma }$是群${\displaystyle G}$的某個凱萊圖，當且僅當${\displaystyle G}$可作為圖自同構（就是要保存邊的集合）作用在${\displaystyle \Gamma }$上，且該作用簡單傳遞。^[1]

要從一個凱萊圖${\displaystyle \Gamma =\Gamma (G,S)}$找回群${\displaystyle G}$和生成集${\displaystyle S}$，先選擇一個頂點${\displaystyle v_{1}\in V(\Gamma )}$，標上群的單位元${\displaystyle e}$。接著，對${\displaystyle \Gamma }$的每個頂點${\displaystyle v}$，${\displaystyle G}$中有唯一元素將${\displaystyle v_{1}}$變換到${\displaystyle v}$，於是可以在${\displaystyle v}$處標記該唯一元素。最後要確定${\displaystyle G}$的哪個生成集${\displaystyle S}$，產生凱萊圖${\displaystyle \Gamma }$，而所求的${\displaystyle S}$就是毗連${\displaystyle v_{1}}$的頂點標記的集合。生成集合是有限（這是凱萊圖的共同假定）當且僅當這個圖是局部有限的（就是說每個頂點僅毗連於有限多條邊）。

• 如果生成集合的成員${\displaystyle s}$是自身的逆元，即${\displaystyle s=s^{-1}}$，則它一般被表示為無向邊。
• 凱萊圖${\displaystyle \Gamma (G,S)}$本質上依賴於如何選擇生成集${\displaystyle S}$。例如，如果生成集合${\displaystyle S}$有${\displaystyle k}$個元素，則凱萊圖的每個頂點都有${\displaystyle k}$條有向邊進入，${\displaystyle k}$條有向邊外出。當生成集合${\displaystyle S}$為對稱集，且有${\displaystyle r}$個元素時，凱萊圖是${\displaystyle r}$度的正則圖。
• 在凱萊圖中的環（“閉合路徑”）指示${\displaystyle S}$的元素之間的關係。在群的凱萊複形此一更複雜的構造中，對應於關係的閉合路徑被用多邊形“填充”。
• 如果${\displaystyle f:G'\to G}$是滿射群同態并且${\displaystyle G'}$的生成集合${\displaystyle S'}$的元素的像是不同的，則導出圖覆疊（英语：Covering graph）映射$${\displaystyle {\bar {f}}:\Gamma (G',S')\to \Gamma (G,S),\quad }$$這里的${\displaystyle S=f(S')}$，特別是，如果群${\displaystyle G}$有${\displaystyle k}$個生成元，階均不為${\displaystyle 2}$，并且這些生成元和它們的逆元構成集合${\displaystyle S}$，則該集合生成的自由群${\displaystyle F(S)}$有到${\displaystyle G}$的滿同態（商映射），故${\displaystyle \Gamma (G,S)}$被自由群的凱萊圖覆蓋，即${\displaystyle 2k}$度的無限正則樹。
• 即使集合${\displaystyle S}$不生成群${\displaystyle G}$，仍可以構造圖${\displaystyle \Gamma (G,S)}$。但是，此情況下，所得的圖並不連通。在這種情況下，這個圖的每個連通分支對應${\displaystyle S}$所生成子群的一個陪集。
• 對于有限凱萊圖（視為無向），其頂點連通性等于這個圖的度的${\displaystyle 2/3}$。若生成集極小（即移除任一元素及其逆元，就不再生成整個群），則其頂點連通性等於度數。^[2]至於邊連通性，則在任何情況下皆等於度數。^[3]
• 群${\displaystyle G}$的每個乘性特徵標（英语：Multiplicative character）${\displaystyle \chi }$都給出${\displaystyle \Gamma (G,S)}$鄰接矩陣的特徵向量。若${\displaystyle G}$為交換群，則對應的特徵值為${\displaystyle \lambda _{\chi }=\sum _{s\in S}\chi (s).}$特別地，平凡特徵標（將所有元素映至常數${\displaystyle 1}$）對應的特徵值，等於${\displaystyle \Gamma (G,S)}$的度數，即${\displaystyle S}$的元素個數。若${\displaystyle G}$為交換群，則恰有${\displaystyle |G|}$個特徵標，故已足以確定全部特徵值。

如果轉而把頂點作為固定子群${\displaystyle H}$的右陪集，就得到了一個有關的構造Schreier陪集圖，它是陪集枚舉或Todd-Coxeter算法的基礎。

研究圖的鄰接矩陣特別是應用譜圖理論的定理能洞察群的結構。

• 群的生成集合
• 群的展示