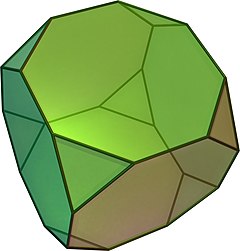
截角立方体

截角立方体

(按這裡觀看旋轉模型)
類別	半正多面體
對偶多面體	三角化八面體
識別
名稱	截角立方体
參考索引	U09, C21, W8
鮑爾斯縮寫 （verse-and-dimensions的wikia：Bowers acronym）	tic
數學表示法
考克斯特符號 （英语：Coxeter-Dynkin diagram）
施萊夫利符號	t{4,3}
威佐夫符號 （英语：Wythoff symbol）	2 3 | 4
康威表示法	tC
性質
面	14
邊	36
頂點	24
歐拉特徵數	F=14, E=36, V=24 （χ=2）
組成與佈局
面的種類	正三角形 正八邊形
面的佈局 （英语：Face configuration）	8個{3} 6個{8}
頂點圖	3.8.8
對稱性
對稱群	Oh群
特性
-
圖像
3.8.8 （頂點圖） 三角化八面體 （對偶多面體） （展開圖）
查 论 编

在幾何學中，截角立方体是一種十四面體，由八個正三角形與六個正八邊形組成，具有14個面、24個頂點以及36條邊。是一種阿基米德立體^[1]，屬於半正多面體。其對偶多面體為三角化八面體。

截角立方體是一種適當截角的立方體。截角時確定了截面的邊與沒截到的長度等長，因此會形成正八邊形。過度截角到最後會變成截半立方體。

截角立方體的對偶多面體是三角化八面體，若截角立方體的邊長是2，則其對偶的邊常會變成${\displaystyle \scriptstyle {2+{\sqrt {2}}}}$單位長。

一個邊長為2ξ、幾何中心位於原點的截角立方體，其頂點座標為：

(±ξ, ±1, ±1),

(±1, ±ξ, ±1),

(±1, ±1, ±ξ)

其中 ξ = ${\displaystyle \scriptstyle {{\sqrt {2}}-1}}$。

參數ξ的值可以在±1之間變化。值為1時產生一個立方體、值為0時是截半立方體，負值會變成自我相交的八角星面。

截角立方體的表面積為${\displaystyle 2(6+6{\sqrt {2}}+{\sqrt {3}})a^{2}}$，體積為${\displaystyle {\frac {1}{3}}(21+14{\sqrt {2}})a^{3}}$，其中${\displaystyle a}$是該截半立方體的邊長^[2]。

表面積 = ${\displaystyle A=2(6+6{\sqrt {2}}+{\sqrt {3}})a^{2}\approx 32.4346644a^{2}}$

體積 = ${\displaystyle V={\frac {1}{3}}(21+14{\sqrt {2}})a^{3}\approx 13.5996633a^{3}}$

將立方體進行截角操作，也就是將立方體的八個頂點切去並在被切掉的地方建立八個正三角形面即可得到一個截角立方體。

截角立方體具有五個特殊正交投影，可分為三大類：以頂點為中心、以邊緣為中心（稜）、以及以面為中心。以頂點為中心僅有一種，以邊緣（稜）為中心有兩種：以三角形-八邊形邊為中心和以八邊形-八邊形邊為中心；以面為中心也是兩種：以三角形面為中心以及以八邊形面為中心。最後兩個對應B₂和A₂考克斯特平面。

截角立方體的正交投影

建立方式	頂點	邊 3-8	邊 8-8	面 八邊形	面 三角形
截角立方體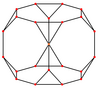
三角化八面體 （對偶多面體）
投影 對稱性	[2]	[2]	[2]	[4]	[6]

	以正八邊形為中心	以正三角形為中心
平行投影	施莱格尔投影（英语：Schlegel diagram）

截角立方體可以分割成一個中央立方體、周圍六個四角帳塔跟角落八個正四面體。這種結構也可以在大斜方截半立方體堆砌中發現，其具有立方體、正四面體以及小斜方截半立方體的胞。

這種分解方式去除兩個四角帳塔和中間的立方體可以用來構造斯圖爾特環形所有正的面，這種「被挖空的」立方體有16個三角形，正方形12，和4個八邊形^[3][4]。

共有三種多面體與截角立方體有著相同的頂點排佈。他們分別為：

截角立方體

非凸大斜方截半立方體

大立方立方八面體

大斜方立方體

截角立方體是立方體經過截角變換後的結果，與立方體相關的多面體還有：

半正正八面体家族多面体

对称性: [4,3], (*432)							[4,3]+, (432)	[1+,4,3], (*332)	[4,3+], (3*2)
{4,3}	t0,1{4,3}	t1{4,3}	t1,2{4,3}	{3,4}	t0,2{4,3}	t0,1,2{4,3}	s{4,3}	h{4,3}	h1,2{4,3}
半正多面体的对偶
V4.4.4	V3.8.8	V3.4.3.4	V4.6.6	V3.3.3.3	V3.4.4.4	V4.6.8	V3.3.3.3.4	V3.3.3	V3.3.3.3.3

此多面體的拓撲結構屬於考克斯特對稱群[n,3]構成的一系列頂點配置為(3.2n.2n)和n.8.8的均勻截角多面體和鑲嵌家族的一部分。

截角立方體的面組成方式是一個正八邊形與正三角形交錯組成。同樣由正多邊形與正三角形交錯組成的多面體或鑲嵌圖包括：

*n32變異對稱性的截角鑲嵌（英语：Template:Truncated figure1 table）: 3.2n.2n

對稱性 *n32 [n,3]	球面鑲嵌（英语：List_of_spherical_symmetry_groups）				歐氏鑲嵌（英语：List_of_planar_symmetry_groups）	緊湊雙曲		非緊雙曲
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
截角鑲嵌
頂點（英语：Vertex configuration）	3.4.4	3.6.6	3.8.8	3.10.10	3.12.12	3.14.14（英语：Truncated_heptagonal_tiling）	3.16.16（英语：Truncated octagonal tiling）	3.∞.∞（英语：Truncated order-3 apeirogonal tiling）
三角化 鑲嵌
頂點（英语：Vertex configuration）	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14（英语：Truncated_heptagonal_tiling#Dual_tiling）	V3.16.16（英语：Truncated_octagonal_tiling#Dual_tiling）	V3.∞.∞（英语：Truncated_order-3_apeirogonal_tiling#Dual_tiling）

如上所述，截角立方體的面組成方式是一個正八邊形與正三角形交錯組成。另外一種就是視為正八邊形與其他正多邊形交錯組成。具有此性質的多面體或鑲嵌圖包括：

*n42變異對稱性的截角鑲嵌: n.8.8

對稱性 *n42（英语：Orbifold notation） [n,4]	球面鑲嵌（英语：List_of_spherical_symmetry_groups）		歐氏鑲嵌（英语：List_of_planar_symmetry_groups）	緊湊雙曲鑲嵌				仿緊雙曲鑲嵌
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
截角 圖
頂點（英语：Vertex configuration）	2.8.8	3.8.8	4.8.8	5.8.8（英语：Truncated order-5 square tiling）	6.8.8（英语：Truncated order-6 square tiling）	7.8.8（英语：Truncated order-7 square tiling）	8.8.8	∞.8.8（英语：Truncated infinite-order square tiling）
n-角化 圖
頂點（英语：Vertex configuration）	V2.8.8	V3.8.8	V4.8.8	V5.8.8	V6.8.8	V7.8.8	V8.8.8	V∞.8.8

截角立方體是將立方體每一個頂點切去，而立方體具有偶數個頂點（8個），且每個面的角數量也是偶數個（正方形有四個角）因此可以進行交錯截角。交錯截角立方體是一個倒角四面體。

截角立方體是截角超方形家族中的第二個成員，相關的多胞體包括：

截角超方形

							...
截角正方形	截角立方體	截角超立方體	截角五维超正方体	截角六維超正方體（英语：Truncated 6-cube）	截角七維超正方體（英语：Truncated 7-cube）	截角八維超正方體（英语：Truncated 8-cube）

• 立方體
• 截半立方體
• 廣義截角立方體

• Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X.  (Section 3-9)
• Cromwell, P. Polyhedra, CUP hbk (1997), pbk. (1999). Ch.2 p.79-86 Archimedean solids

• 埃里克·韦斯坦因, 截角立方体 （參閱阿基米德立體） 於MathWorld（英文）
  • 埃里克·韦斯坦因. Truncated cubical graph. MathWorld. 
• Klitzing, Richard. 3D convex uniform polyhedra o3x4x - tic. bendwavy.org. 
• Editable printable net of a truncated cube with interactive 3D view （页面存档备份，存于互联网档案馆）
• The Uniform Polyhedra （页面存档备份，存于互联网档案馆）
• Virtual Reality Polyhedra （页面存档备份，存于互联网档案馆） www.georgehart.com: The Encyclopedia of Polyhedra
  • VRML model （页面存档备份，存于互联网档案馆）
  • Conway Notation for Polyhedra （页面存档备份，存于互联网档案馆） Try: "tC"