Dicyclic group

Algebraic structure → Group theory Group theory
Basic notions Subgroup Normal subgroup Group action Quotient group (Semi-)direct product Direct sum Free product Wreath product Group homomorphisms kernel image simple finite infinite continuous multiplicative additive cyclic abelian dihedral nilpotent solvable Glossary of group theory List of group theory topics
Finite groups Cyclic group Zn Symmetric group Sn Alternating group An Dihedral group Dn Quaternion group Q Cauchy's theorem Lagrange's theorem Sylow theorems Hall's theorem p-group Elementary abelian group Frobenius group Schur multiplier Classification of finite simple groups cyclic alternating Lie type sporadic
Discrete groups Lattices Integers (${\displaystyle \mathbb {Z} }$) Free group Modular groups PSL(2, ${\displaystyle \mathbb {Z} }$) SL(2, ${\displaystyle \mathbb {Z} }$) Arithmetic group Lattice Hyperbolic group
Topological and Lie groups Solenoid Circle General linear GL(n) Special linear SL(n) Orthogonal O(n) Euclidean E(n) Special orthogonal SO(n) Unitary U(n) Special unitary SU(n) Symplectic Sp(n) G2 F4 E6 E7 E8 Lorentz Poincaré Conformal Diffeomorphism Loop Infinite dimensional Lie group O(∞) SU(∞) Sp(∞)
Algebraic groups Linear algebraic group Reductive group Abelian variety Elliptic curve
v t e

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Dicyclic group" – news · newspapers · books · scholar · JSTOR (February 2010) (Learn how and when to remove this message)

In group theory, a dicyclic group (notation Dic_n or Q_4n,^[1] ⟨n,2,2⟩^[2]) is a particular kind of non-abelian group of order 4n (n > 1). It is an extension of the cyclic group of order 2 by a cyclic group of order 2n, giving the name di-cyclic. In the notation of exact sequences of groups, this extension can be expressed as:

${\displaystyle 1\to C_{2n}\to {\mbox{Dic}}_{n}\to C_{2}\to 1.\,}$

More generally, given any finite abelian group with an order-2 element, one can define a dicyclic group.

For each integer n > 1, the dicyclic group Dic_n can be defined as the subgroup of the unit quaternions generated by

${\displaystyle {\begin{aligned}a&=e^{\frac {i\pi }{n}}=\cos {\frac {\pi }{n}}+i\sin {\frac {\pi }{n}}\\x&=j\end{aligned}}}$

More abstractly, one can define the dicyclic group Dic_n as the group with the following presentation^[3]

${\displaystyle \operatorname {Dic} _{n}=\left\langle a,x\mid a^{2n}=1,\ x^{2}=a^{n},\ x^{-1}ax=a^{-1}\right\rangle .\,\!}$

Some things to note which follow from this definition:

• ${\displaystyle x^{4}=1}$
• ${\displaystyle x^{2}a^{m}=a^{m+n}=a^{m}x^{2}}$
• if ${\displaystyle l=\pm 1}$, then ${\displaystyle x^{l}a^{m}=a^{-m}x^{l}}$
• ${\displaystyle a^{m}x^{-1}=a^{m-n}a^{n}x^{-1}=a^{m-n}x^{2}x^{-1}=a^{m-n}x}$

Thus, every element of Dic_n can be uniquely written as a^mx^l, where 0 ≤ m < 2n and l = 0 or 1. The multiplication rules are given by

• ${\displaystyle a^{k}a^{m}=a^{k+m}}$
• ${\displaystyle a^{k}a^{m}x=a^{k+m}x}$
• ${\displaystyle a^{k}xa^{m}=a^{k-m}x}$
• ${\displaystyle a^{k}xa^{m}x=a^{k-m+n}}$

It follows that Dic_n has order 4n.^[3]

When n = 2, the dicyclic group is isomorphic to the quaternion group Q. More generally, when n is a power of 2, the dicyclic group is isomorphic to the generalized quaternion group.^[3]

For each n > 1, the dicyclic group Dic_n is a non-abelian group of order 4n. (For the degenerate case n = 1, the group Dic₁ is the cyclic group C₄, which is not considered dicyclic.)

Let A = ⟨a⟩ be the subgroup of Dic_n generated by a. Then A is a cyclic group of order 2n, so [Dic_n:A] = 2. As a subgroup of index 2 it is automatically a normal subgroup. The quotient group Dic_n/A is a cyclic group of order 2.

Dic_n is solvable; note that A is normal, and being abelian, is itself solvable.

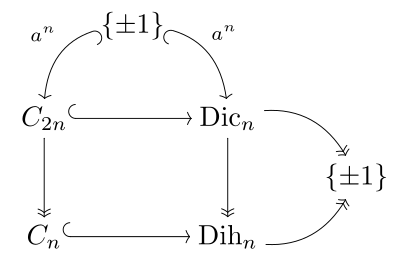
The dicyclic group is a binary polyhedral group — it is one of the classes of subgroups of the Pin group Pin₋(2), which is a subgroup of the Spin group Spin(3) — and in this context is known as the binary dihedral group.

The connection with the binary cyclic group C_2n, the cyclic group C_n, and the dihedral group Dih_n of order 2n is illustrated in the diagram at right, and parallels the corresponding diagram for the Pin group. Coxeter writes the binary dihedral group as ⟨2,2,n⟩ and binary cyclic group with angle-brackets, ⟨n⟩.

There is a superficial resemblance between the dicyclic groups and dihedral groups; both are a sort of "mirroring" of an underlying cyclic group. But the presentation of a dihedral group would have x² = 1, instead of x² = aⁿ; and this yields a different structure. In particular, Dic_n is not a semidirect product of A and ⟨x⟩, since A ∩ ⟨x⟩ is not trivial.

The dicyclic group has a unique involution (i.e. an element of order 2), namely x² = aⁿ. Note that this element lies in the center of Dic_n. Indeed, the center consists solely of the identity element and x². If we add the relation x² = 1 to the presentation of Dic_n one obtains a presentation of the dihedral group Dih_n, so the quotient group Dic_n/<x²> is isomorphic to Dih_n.

There is a natural 2-to-1 homomorphism from the group of unit quaternions to the 3-dimensional rotation group described at quaternions and spatial rotations. Since the dicyclic group can be embedded inside the unit quaternions one can ask what the image of it is under this homomorphism. The answer is just the dihedral symmetry group Dih_n. For this reason the dicyclic group is also known as the binary dihedral group. Note that the dicyclic group does not contain any subgroup isomorphic to Dih_n.

The analogous pre-image construction, using Pin₊(2) instead of Pin₋(2), yields another dihedral group, Dih_2n, rather than a dicyclic group.

Let A be an abelian group, having a specific element y in A with order 2. A group G is called a generalized dicyclic group, written as Dic(A, y), if it is generated by A and an additional element x, and in addition we have that [G:A] = 2, x² = y, and for all a in A, x⁻¹ax = a⁻¹.

Since for a cyclic group of even order, there is always a unique element of order 2, we can see that dicyclic groups are just a specific type of generalized dicyclic group.

The dicyclic group is the case ${\displaystyle (p,q,r)=(2,2,n)}$ of the family of binary triangle groups ${\displaystyle \Gamma (p,q,r)}$ defined by the presentation:[1]

${\displaystyle \langle a,b,c\mid a^{p}=b^{q}=c^{r}=abc\rangle .}$

Taking the quotient by the additional relation ${\displaystyle abc=e}$ produces an ordinary triangle group, which in this case is the dihedral quotient ${\displaystyle \mathrm {Dic} _{n}\rightarrow \mathrm {Dih} _{n}}$.

• binary polyhedral group
• binary cyclic group, ⟨n⟩, order 2n
• binary tetrahedral group, 2T = ⟨2,3,3⟩,^[2] order 24
• binary octahedral group, 2O = ⟨2,3,4⟩,^[2] order 48
• binary icosahedral group, 2I = ⟨2,3,5⟩,^[2] order 120

• Dicyclic groups on GroupNames