Criptografia

Criptografia, ou criptologia (do grego antigo: κρυπτός, romanizado: kryptós "oculto, secreto"; e γράφειν graphein, "escrever", ou -λογία -logia, "estudo", respectivamente^[1]), é a prática e o estudo de técnicas para comunicação segura na presença de comportamento adversário.^[2] De forma mais geral, a criptografia trata da construção e análise de protocolos que impedem terceiros ou o público de ler mensagens privadas.^[3] A criptografia moderna existe na intersecção das disciplinas de matemática, ciência da computação, segurança da informação, engenharia elétrica, processamento de sinais digitais, física e outras.^[4] Conceitos básicos relacionados à segurança da informação (confidencialidade de dados, integridade de dados, autenticação e não repúdio) também são centrais para a criptografia.^[5] As aplicações práticas da criptografia incluem comércio eletrônico, cartões de pagamento baseados em chip, moedas digitais, senhas de computador e comunicações militares.

Criptografia antes da era moderna era efetivamente sinônimo de cifragem, convertendo informações legíveis (texto simples) em texto sem sentido ininteligível (texto cifrado), que só pode ser lido revertendo o processo (decifragem). O remetente de uma mensagem cifrada (codificada) compartilha a técnica de decifragem (decodificação) apenas com os destinatários pretendidos para impedir o acesso de adversários. A literatura de criptografia geralmente usa os nomes "Alice" (ou "A") para o remetente, "Bob" (ou "B") para o destinatário pretendido e "Eve" (ou "E") para o adversário espião.^[6] Desde o desenvolvimento das máquinas de cifrar de rotor na Primeira Guerra Mundial e o advento dos computadores na Segunda Guerra Mundial, os métodos de criptografia se tornaram cada vez mais complexos e suas aplicações mais variadas.

A criptografia moderna é fortemente baseada em teoria matemática e prática de ciência da computação; algoritmos criptográficos são projetados em torno de suposições de dificuldade/dureza computacional, tornando tais algoritmos difíceis de serem quebrados na prática real por qualquer adversário. Embora seja teoricamente possível invadir um sistema bem projetado, é inviável na prática real fazê-lo. Tais esquemas, se bem projetados, são, portanto, denominados "computacionalmente seguros". Avanços teóricos (por exemplo, melhorias em algoritmos de fatoração de inteiros) e tecnologia de computação mais rápida exigem que esses designs sejam continuamente reavaliados e, se necessário, adaptados. Esquemas teoricamente seguros de informações que comprovadamente não podem ser quebrados mesmo com poder de computação ilimitado, como a cifra de único uso (OTP), são muito mais difíceis de usar na prática do que os melhores esquemas teoricamente quebráveis, mas computacionalmente seguros.

O crescimento da tecnologia criptográfica levantou uma série de questões legais na Era da Informação. O potencial da criptografia para uso como uma ferramenta de espionagem e sedição levou muitos governos a classificá-la como uma arma e a limitar ou mesmo proibir seu uso e exportação.^[7] Em algumas jurisdições onde o uso da criptografia é legal, as leis permitem que os investigadores obriguem a divulgação de chaves de encriptação para documentos relevantes para uma investigação.^[8][9] A criptografia também desempenha um papel importante na gestão de direitos digitais e disputas de violação de direitos autorais com relação à mídia digital.^[10]

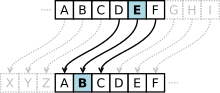
O primeiro uso do termo "criptografia" (em oposição a "criptograma") remonta ao século XIX — originário de "O Escaravelho de Ouro", uma história de Edgar Allan Poe.^[11][12]

Até os tempos modernos, criptografia se referia quase exclusivamente à "cifragem", que é o processo de conversão de informações comuns (chamadas de textos simples) em uma forma ininteligível (chamada de texto cifrado).^[13] A decifragem é o inverso, em outras palavras, mover-se do texto cifrado ininteligível de volta para o texto simples. Uma cifra é um par de algoritmos que realizam a cifragem e a decifragem reversa. A operação detalhada de uma cifra é controlada tanto pelo algoritmo quanto, em cada instância, por uma "chave". A chave é um segredo (idealmente conhecido apenas pelos comunicantes), geralmente uma sequência de caracteres (idealmente curta para que possa ser lembrada pelo usuário), que é necessária para decifar o texto cifrado. Em termos matemáticos formais, um "criptossistema" é a lista ordenada de elementos de textos simples finitos possíveis, textos cifrados finitos possíveis, chaves finitas possíveis e os algoritmos de cifragem e decifragem que correspondem a cada chave. Chaves são importantes tanto formalmente quanto na prática real, pois cifras sem chaves variáveis ​​podem ser quebradas trivialmente com apenas o conhecimento da cifra usada e, portanto, são inúteis (ou até mesmo contraproducentes) para a maioria dos propósitos. Historicamente, cifras eram frequentemente usadas diretamente para cifragem ou decifragem sem procedimentos adicionais, como autenticação ou verificações de integridade.

Existem dois tipos principais de criptossistemas: simétricos e assimétricos. Em sistemas simétricos, os únicos conhecidos até a década de 1970, a mesma chave secreta cifra e decifra uma mensagem. A manipulação de dados em sistemas simétricos é significativamente mais rápida do que em sistemas assimétricos. Os sistemas assimétricos usam uma "chave pública" para cifrar uma mensagem e uma "chave privada" relacionada para a decifrar. A vantagem dos sistemas assimétricos é que a chave pública pode ser publicada livremente, permitindo que as partes estabeleçam uma comunicação segura sem ter uma chave secreta compartilhada. Na prática, os sistemas assimétricos são usados ​​para primeiro trocar uma chave secreta e, em seguida, a comunicação segura prossegue por meio de um sistema simétrico mais eficiente usando essa chave.^[14] Exemplos de sistemas assimétricos incluem a troca de chaves de Diffie e Hellman, RSA (Rivest, Shamir, e Adleman), ECC (Criptografia de Curva Elíptica) e criptografia pós-quântica. Algoritmos simétricos seguros incluem o AES (Padrão de Cifragem Avançada) comumente usado, que substituiu o antigo DES (Padrão de Cifragem de Dados).^[15] Algoritmos simétricos inseguros incluem esquemas de emaranhamento de linguagem infantis, como Pig Latin ou outros jargões, e todos os esquemas criptográficos históricos, por mais seriamente pretendidos, anteriores à invenção da cifra de uso único no início do século XX.

No uso coloquial, o termo "código" é frequentemente usado para significar qualquer método de cifragem ou ocultação de significado. No entanto, na criptografia, código tem um significado mais específico: a substituição de uma unidade de texto simples (ou seja, uma palavra ou frase significativa) por uma palavra de código (por exemplo, "wallaby" substitui "ataque ao amanhecer"). Uma cifra, em contraste, é um esquema para alterar ou substituir um elemento abaixo de tal nível (uma letra, uma sílaba ou um par de letras, etc.) para produzir um texto cifrado.

Criptoanálise é o termo usado para o estudo de métodos para obter o significado de informações cifradas sem acesso à chave normalmente necessária para isso; ou seja, é o estudo de como "quebrar" algoritmos de cifragem ou suas implementações.

Alguns usam os termos "criptografia" e "criptologia" alternadamente em inglês,^[16] enquanto outros (incluindo a prática militar dos EUA em geral) usam "criptografia" para se referir especificamente ao uso e à prática de técnicas criptográficas e "criptologia" para se referir ao estudo combinado de criptografia e criptoanálise.^[17][18] O inglês é mais flexível do que várias outras línguas nas quais "criptologia" (feita por criptologistas) é sempre usada no segundo sentido acima. A RFC 2828 informa que a esteganografia às vezes é incluída na criptologia.^[19]

O estudo das características das línguas que têm alguma aplicação em criptografia ou criptologia (por exemplo, dados de frequência, combinações de letras, padrões universais, etc.) é chamado de criptolinguística. A criptolinguística é especialmente usada em aplicações de inteligência militar para decifrar comunicações estrangeiras.^[20][21]

Ver artigo principal: História da criptografia

Antes da era moderna, a criptografia focava na confidencialidade da mensagem (ou seja, cifragem) — conversão de mensagens de uma forma compreensível para uma incompreensível e de volta na outra ponta, tornando-a ilegível por interceptadores ou bisbilhoteiros sem conhecimento secreto (ou seja, a chave necessária para decifrar essa mensagem). A cifragem tentava garantir o sigilo nas comunicações, como as de espiões, líderes militares e diplomatas. Nas últimas décadas, o campo se expandiu além das preocupações com a confidencialidade para incluir técnicas de verificação de integridade de mensagens, autenticação de identidade de remetente/destinatário, assinaturas digitais, provas interativas e computação segura, entre outras.

Os principais tipos de cifras clássicas são cifras de transposição, que reorganizam a ordem das letras em uma mensagem (por exemplo, "hello world" se torna "ehlol owrdl" em um esquema de rearranjo trivialmente simples) e cifras de substituição, que substituem sistematicamente letras ou grupos de letras por outras letras ou grupos de letras (por exemplo, "voar de uma vez" se torna "wpbs ef vnb wfa" substituindo cada letra pela seguinte no alfabeto latino).^[22] Versões simples de qualquer uma delas nunca ofereceram muita confidencialidade de oponentes empreendedores. Uma cifra de substituição inicial foi a cifra de César, na qual cada letra no texto simples era substituída por uma letra com um número fixo de posições mais abaixo no alfabeto. Suetônio relata que Júlio César a usava com um deslocamento de três para se comunicar com seus generais. A Atbash é um exemplo de uma cifra hebraica inicial. O primeiro uso conhecido da criptografia é algum texto cifrado esculpido em pedra no Egito (c. 1900 a.E.C.), mas isso pode ter sido feito para a diversão de observadores letrados e não como uma forma de ocultar informações.

Diz-se que os gregos dos tempos clássicos conheciam cifras (por exemplo, a cifra de transposição da cítala que se alega ter sido usada pelos militares espartanos).^[23] A esteganografia (ou seja, esconder até mesmo a existência de uma mensagem para mantê-la confidencial) também foi desenvolvida pela primeira vez nos tempos antigos. Um exemplo antigo, de Heródoto, foi uma mensagem tatuada na cabeça raspada de um escravo e escondida sob o cabelo crescido.^[13] Outros métodos de esteganografia envolvem "esconder-se à vista de todos", como usar uma cifra musical para disfarçar uma mensagem criptografada dentro de uma partitura regular. Exemplos mais modernos de esteganografia incluem o uso de tinta invisível, micropontos e marcas d'água digitais para ocultar informações.

Na Índia, o Kama Sutra de Vātsyāyana, de 2000 anos, fala de dois tipos diferentes de cifras chamadas Kautiliyam e Mulavediya. No Kautiliyam, as substituições de letras da cifra são baseadas em relações fonéticas, como vogais se tornando consoantes. No Mulavediya, o alfabeto da cifra consiste em parear letras e usar as recíprocas.^[13]

Na Pérsia Sassânida, havia duas escritas secretas, de acordo com o autor muçulmano Ibn al-Nadim: a šāh-dabīrīya (literalmente "escrita do rei"), que era usada para correspondência oficial, e a rāz-saharīya, que era usada para comunicar mensagens secretas com outros países.^[24]

David Kahn observa em The Codebreakers que a criptologia moderna se originou entre os árabes, o primeiro povo a documentar sistematicamente métodos criptoanalíticos.^[25] Al-Khalil (717–786) escreveu o Livro de Mensagens Criptográficas, que contém o primeiro uso de permutações e combinações para listar todas as palavras árabes possíveis com e sem vogais.^[26]

Textos cifrados produzidos por uma cifra clássica (e algumas cifras modernas) revelarão informações estatísticas sobre o texto simples, e essas informações podem frequentemente ser usadas para quebrar a cifra. Após a descoberta da análise de frequência, quase todas essas cifras puderam ser quebradas por um invasor informado. Essas cifras clássicas ainda desfrutam de popularidade hoje, embora principalmente como quebra-cabeças (ver criptograma). O polímata e matemático árabe Al-Kindi escreveu um livro sobre criptografia intitulado Risalah fi Istikhraj al-Mu'amma (Manuscrito para a Decifrar Mensagens Criptográficas), que descreveu o primeiro uso conhecido de técnicas de criptoanálise de análise de frequência.^[27][28]

As frequências de letras de idioma podem oferecer pouca ajuda para algumas técnicas de criptografia histórica estendidas, como a cifra homofônica, que tende a achatar a distribuição de frequência. Para essas cifras, as frequências de grupos de letras de idioma (ou n-grama) podem fornecer um ataque.

Essencialmente todas as cifras permaneceram vulneráveis ​​à criptoanálise usando a técnica de análise de frequência até o desenvolvimento da cifra polialfabética, mais claramente por Leon Battista Alberti por volta do ano de 1467, embora haja alguma indicação de que já era conhecida por Al-Kindi.^[28] A inovação de Alberti foi usar diferentes cifras (ou seja, alfabetos de substituição) para várias partes de uma mensagem (talvez para cada letra de texto simples sucessiva no limite). Ele também inventou o que provavelmente foi o primeiro dispositivo cifrador automático, uma roda que implementou uma realização parcial de sua invenção. Na cifra de Vigenère, uma cifra polialfabética, a cifragem usa uma palavra-chave, que controla a substituição de letras dependendo de qual letra da palavra-chave é usada. Em meados do século XIX, Charles Babbage mostrou que a cifra de Vigenère era vulnerável ao exame de Kasiski, mas isso foi publicado pela primeira vez cerca de dez anos depois por Friedrich Kasiski.^[29]

Embora a análise de frequência possa ser uma técnica poderosa e geral contra muitas cifras, a cifragem ainda tem sido eficaz na prática, pois muitos aspirantes a criptoanalistas não tinham conhecimento da técnica. Quebrar uma mensagem sem usar a análise de frequência essencialmente exigia conhecimento da cifra usada e talvez da chave envolvida, tornando assim a espionagem, o suborno, o roubo, a deserção, etc., abordagens mais atraentes para os desinformados criptoanaliticamente. Foi finalmente reconhecido explicitamente no século XIX que o sigilo do algoritmo de uma cifra não é uma salvaguarda sensata nem prática da segurança da mensagem; na verdade, percebeu-se ainda que qualquer esquema criptográfico adequado (incluindo cifras) deve permanecer seguro mesmo que o adversário entenda completamente o algoritmo da cifra em si. A segurança da chave usada deve ser suficiente para que uma boa cifra mantenha a confidencialidade sob um ataque. Este princípio fundamental foi declarado explicitamente pela primeira vez em 1883 por Auguste Kerckhoffs e é geralmente chamado de Princípio de Kerckhoffs; alternativamente e de forma mais direta, foi reafirmado por Claude Shannon, o inventor da teoria da informação e dos fundamentos da criptografia teórica, como a Máxima de Shannon — "o inimigo conhece o sistema".

Diferentes dispositivos físicos e auxílios foram usados ​​para auxiliar com cifras. Um dos primeiros pode ter sido a cítala da Grécia antiga, uma haste supostamente usada pelos espartanos como auxílio para uma cifra de transposição. Na época medieval, outros auxílios foram inventados, como a grade de cifras, que também era usada para um tipo de esteganografia. Com a invenção da cifra polialfabética, vieram auxílios mais sofisticados, como o próprio disco de cifras de Alberti, o esquema de tabula recta de Johannes Trithemius e a roda cifradora de Thomas Jefferson (não conhecida publicamente e reinventada independentemente por Bazeries por volta de 1900). Muitos dispositivos mecânicos de cifragem/decifragem foram inventados no início do século XX e vários patenteados, entre eles máquinas de rotor — incluindo a famosa máquina Enigma usada pelo governo e pelos militares alemães no final da década de 1920 e durante a Segunda Guerra Mundial.^[30] As cifras implementadas por exemplos de melhor qualidade desses projetos de máquinas trouxeram um aumento substancial na dificuldade criptanalítica após a Primeira Guerra Mundial.^[31]

A criptoanálise dos novos dispositivos mecânicos de cifragem provou ser difícil e trabalhosa. No Reino Unido, os esforços criptoanalíticos em Bletchley Park durante a Segunda Guerra Mundial estimularam o desenvolvimento de meios mais eficientes para realizar tarefas repetitivas, como a quebra de códigos militares (decifragem). Isso culminou no desenvolvimento do Colossus, o primeiro computador totalmente eletrônico, digital e programável do mundo, que auxiliou na decifração de cifras geradas pela máquina Lorenz SZ40/42 do Exército Alemão.

A extensa pesquisa acadêmica aberta sobre criptografia é relativamente recente, começando em meados da década de 1970. No início da década de 1970, o pessoal da IBM projetou o algoritmo Padrão de Cifragem de Dados (DES) que se tornou o primeiro padrão de criptografia do governo federal nos Estados Unidos.^[32] Em 1976, Whitfield Diffie e Martin Hellman publicaram o algoritmo de troca de chaves de Diffie e Hellman.^[33] Em 1977, o algoritmo de RSA foi publicado na coluna de Martin Gardner na Scientific American.^[34] Desde então, a criptografia se tornou uma ferramenta amplamente usada em comunicações, redes de computadores e segurança de computadores em geral.

Algumas técnicas criptográficas modernas só conseguem manter suas chaves em segredo se certos problemas matemáticos forem intratáveis, como os problemas de logaritmo discreto ou a fatoração de inteiros, então há conexões profundas com a matemática abstrata. Existem muito poucos criptossistemas que são comprovadamente incondicionalmente seguros. A cifra de uso único é um deles, e foi comprovado por Claude Shannon. Existem alguns algoritmos importantes que foram comprovados como seguros sob certas suposições. Por exemplo, a inviabilidade de fatorar inteiros extremamente grandes é a base para acreditar que o de RSA é seguro, e alguns outros sistemas, mas mesmo assim, a prova de inquebrabilidade não está disponível, pois o problema matemático subjacente permanece aberto. Na prática, eles são amplamente usados, e são considerados inquebráveis ​​na prática pela maioria dos observadores competentes. Existem sistemas semelhantes ao de RSA, como um de Michael O. Rabin, que são comprovadamente seguros, desde que a fatoração n = pq seja impossível; é bastante inutilizável na prática. O problema do logaritmo discreto é a base para acreditar que alguns outros criptossistemas são seguros e, novamente, existem sistemas relacionados e menos práticos que são comprovadamente seguros em relação ao problema do logaritmo discreto de solubilidade ou insolvência.^[35]

Além de estar ciente da história criptográfica, os projetistas de sistemas e algoritmos criptográficos também devem considerar sensatamente os prováveis ​​desenvolvimentos futuros enquanto trabalham em seus projetos. Por exemplo, melhorias contínuas no poder de processamento do computador aumentaram o escopo de ataques de força bruta, então, ao especificar comprimentos de chave, os comprimentos de chave necessários estão avançando de forma semelhante.^[36] O impacto potencial da computação quântica já está sendo considerado por alguns projetistas de sistemas criptográficos que desenvolvem criptografia pós-quântica. A anunciada iminência de pequenas implementações dessas máquinas pode estar tornando a necessidade de cautela preventiva mais do que meramente especulativa.^[5]

Antes do início do século XX, a criptografia estava principalmente preocupada com padrões linguísticos e lexicográficos. Desde então, a criptografia ampliou seu escopo e agora faz uso extensivo de subdisciplinas matemáticas, incluindo teoria da informação, complexidade computacional, estatística, combinatória, álgebra abstrata, teoria dos números e matemática finita.^[37] A criptografia também é um ramo da engenharia, mas incomum, pois lida com oposição ativa, inteligente e malévola; outros tipos de engenharia (por exemplo, engenharia civil ou química) precisam lidar apenas com forças naturais neutras. Há também pesquisas ativas examinando a relação entre problemas criptográficos e física quântica.

Assim como o desenvolvimento de computadores digitais e eletrônicos ajudou na criptoanálise, tornou possível cifras muito mais complexas. Além disso, os computadores permitiram a cifragem de qualquer tipo de dado representável em qualquer formato binário, ao contrário das cifras clássicas que cifravam apenas textos em linguagem escrita; isso era novo e significativo. O uso do computador suplantou, portanto, a criptografia linguística, tanto para o design de cifras quanto para a criptoanálise. Muitas cifras de computador podem ser caracterizadas por sua operação em sequências de bits binários (às vezes em grupos ou blocos), diferentemente de esquemas clássicos e mecânicos, que geralmente manipulam caracteres tradicionais (ou seja, letras e dígitos) diretamente. No entanto, os computadores também auxiliaram a criptoanálise, o que compensou até certo ponto a maior complexidade das cifras. No entanto, boas cifras modernas ficaram à frente da criptoanálise; é tipicamente o caso de que o uso de uma cifra de qualidade é muito eficiente (ou seja, rápido e requer poucos recursos, como memória ou capacidade de CPU), enquanto quebrá-la requer um esforço muitas ordens de magnitude maior, e muito maior do que o necessário para qualquer cifra clássica, tornando a criptoanálise tão ineficiente e impraticável a ponto de ser efetivamente impossível.

Ver artigo principal: Algoritmo de chave simétrica

Criptografia de chave simétrica refere-se a métodos de cifragem nos quais tanto o remetente quanto o destinatário compartilham a mesma chave (ou, menos comumente, nos quais suas chaves são diferentes, mas relacionadas de uma forma facilmente computável). Este foi o único tipo de cifragem conhecido publicamente até junho de 1976.^[33]

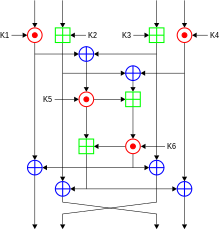
Cifras de chave simétrica são implementadas como cifras de bloco ou cifras de fluxo. Uma cifra de bloco codifica a entrada em blocos de texto simples, em vez de em caracteres individuais, a forma de entrada usada por uma cifra de fluxo.

O Padrão de Cifragem de Dados (DES) e o Padrão de Cifragem Avançada (AES) são projetos de cifras de bloco que foram designados padrões de criptografia pelo governo dos EUA (embora a designação do DES tenha sido finalmente retirada após a adoção do AES).^[38] Apesar de sua depreciação como um padrão oficial, o DES (especialmente sua variante 3DES ainda aprovada e muito mais segura) continua bastante popular; ele é usado em uma ampla gama de aplicações, desde criptografia de ATM^[39] até privacidade de e-mail^[40] e acesso remoto seguro.^[41] Muitas outras cifras de bloco foram projetadas e lançadas, com considerável variação em qualidade. Muitas, até mesmo algumas projetadas por profissionais capazes, foram completamente quebradas, como o FEAL.^[5][42]

Cifras de fluxo, em contraste com o tipo de "bloco", criam um fluxo arbitrariamente longo de material de chave, que é combinado com o texto simples bit a bit ou caractere a caractere, algo como a cifra de uso único. Em uma cifra de fluxo, o fluxo de saída é criado com base em um estado interno oculto que muda conforme a cifradora opera. Esse estado interno é inicialmente configurado usando o material de chave secreta. A RC4 é uma cifra de fluxo amplamente usada.^[5] Cifras de bloco podem ser usadas como cifras de fluxo gerando blocos de um fluxo de chaves (no lugar de um gerador de números pseudoaleatórios) e aplicando uma operação XOR a cada bit do texto simples com cada bit do fluxo de chaves.^[43]

Os códigos de autenticação de mensagens (MACs) são muito parecidos com funções de hash criptográficas, exceto que uma chave secreta pode ser usada para autenticar o valor de hash após o recebimento;^[5][44] essa complicação adicional bloqueia um esquema de ataque contra algoritmos de resumo simples e, portanto, foi considerada válida. As funções de hash criptográficas são um terceiro tipo de algoritmo criptográfico. Elas recebem uma mensagem de qualquer tamanho como entrada e produzem um hash curto de tamanho fixo, que pode ser usado em (por exemplo) uma assinatura digital. Para boas funções de hash, um invasor não consegue encontrar duas mensagens que produzem o mesmo hash. O MD4 é uma função de hash usada há muito tempo que agora está quebrada; o MD5, uma variante reforçada do MD4, também é amplamente usada, mas quebrada na prática. A Agência de Segurança Nacional dos EUA desenvolveu a série Algoritmo de Hash Seguro (SHA) de funções de hash semelhantes ao MD5: O SHA-0 era um algoritmo falho que a agência retirou; o SHA-1 é amplamente implantado e mais seguro que o MD5, mas criptoanalistas identificaram ataques contra ele; a família SHA-2 melhora o SHA-1, mas é vulnerável a conflitos desde de 2011; e a autoridade de padrões dos EUA achou "prudente" de uma perspectiva de segurança desenvolver um novo padrão para "melhorar significativamente a robustez do kit de ferramentas do algoritmo de hash geral do NIST."^[45] Assim, uma competição de design de função de hash foi criada para selecionar um novo padrão nacional dos EUA, a ser chamado de SHA-3, até 2012. A competição terminou em 2 de outubro de 2012, quando o NIST anunciou que Keccak seria o novo algoritmo de hash SHA-3.^[46] Ao contrário das cifras de bloco e fluxo que são invertíveis, as funções de hash criptográficas produzem uma saída com hash que não pode ser usada para recuperar os dados de entrada originais. As funções de hash criptográficas são usadas para verificar a autenticidade dos dados recuperados de uma fonte não confiável ou para adicionar uma camada de segurança.

Ver artigo principal: Criptografia de chave pública

Os criptossistemas de chave simétrica usam a mesma chave para cifragem e decifragem de uma mensagem, embora uma mensagem ou grupo de mensagens possa ter uma chave diferente das outras. Uma desvantagem significativa das cifras simétricas é o gerenciamento de chaves necessário para usá-las com segurança. Cada par distinto de partes comunicantes deve, idealmente, compartilhar uma chave diferente, e talvez para cada texto cifrado trocado também. O número de chaves necessárias aumenta conforme o quadrado do número de membros da rede, o que muito rapidamente requer esquemas complexos de gerenciamento de chaves para mantê-los todos consistentes e secretos.

Em um artigo inovador de 1976, Whitfield Diffie e Martin Hellman propuseram a noção de criptografia de chave pública (também, mais genericamente, chamada de chave assimétrica) na qual duas chaves diferentes, mas matematicamente relacionadas, são usadas — uma chave pública e uma chave privada.^[47] Um sistema de chave pública é construído de forma que o cálculo de uma chave (a "chave privada") é computacionalmente inviável a partir da outra (a "chave pública"), mesmo que elas sejam necessariamente relacionadas. Em vez disso, ambas as chaves são geradas secretamente, como um par inter-relacionado.^[48] O historiador David Kahn descreveu a criptografia de chave pública como "o conceito novo mais revolucionário no campo desde que a substituição polialfabética surgiu no Renascimento".^[49]

Em sistemas de criptografia de chave pública, a chave pública pode ser distribuída livremente, enquanto sua chave privada pareada deve permanecer secreta. Em um sistema de cifragem de chave pública, a chave pública é usada para cifragem, enquanto a chave privada ou secreta é usada para decifragem. Embora Diffie e Hellman não tenham conseguido encontrar tal sistema, eles mostraram que a criptografia de chave pública era de fato possível ao apresentar o protocolo de troca de chaves de Diffie e Hellman, uma solução que agora é amplamente usada em comunicações seguras para permitir que duas partes concordem secretamente em uma chave de cifragem compartilhada.^[33] O padrão X.509 define o formato mais comumente usado para certificados de chave pública.^[50]

A publicação de Diffie e Hellman desencadeou esforços acadêmicos generalizados para encontrar um sistema prático de criptografia de chave pública. Esta corrida foi finalmente vencida em 1978 por Ronald Rivest, Adi Shamir e Len Adleman, cuja solução desde então se tornou conhecida como algoritmo de RSA.^[51]

Os algoritmos de Diffie e Hellman e de RSA, além de serem os primeiros exemplos publicamente conhecidos de algoritmos de chave pública de alta qualidade, estão entre os mais amplamente usados. Outros incluem o sistema criptográfico de Cramer e Shoup, cifragem de ElGamal e várias técnicas de curva elíptica.

Um documento publicado em 1997 pela Sede de Comunicações Governamentais (GCHQ), uma organização de inteligência britânica, revelou que os criptógrafos da GCHQ haviam antecipado vários desenvolvimentos acadêmicos.^[52] Alegadamente, por volta de 1970, James H. Ellis havia concebido os princípios da criptografia de chave assimétrica. Em 1973, Clifford Cocks inventou uma solução que era muito semelhante em lógica de design ao de RSA.^[52][53] Em 1974, Malcolm J. Williamson é alegado ter desenvolvido a troca de chaves de Diffie e Hellman.^[54]

A criptografia de chave pública também é usada para implementar esquemas de assinatura digital. Uma assinatura digital é uma reminiscência de uma assinatura comum; ambas têm a característica de serem fáceis de produzir para um usuário, mas difíceis de falsificar para qualquer outra pessoa. As assinaturas digitais também podem ser permanentemente vinculadas ao conteúdo da mensagem que está sendo assinada; elas não podem ser "movidas" de um documento para outro, pois qualquer tentativa será detectável. Em esquemas de assinatura digital, há dois algoritmos: um para assinatura, no qual uma chave secreta é usada para processar a mensagem (ou um hash da mensagem, ou ambos), e um para verificação, no qual a chave pública correspondente é usada com a mensagem para verificar a validade da assinatura. O de RSA e o Algoritmo de Assinatura Digital (DSA) são dois dos esquemas de assinatura digital mais populares. As assinaturas digitais são centrais para a operação de infraestruturas de chaves públicas e muitos esquemas de segurança de rede (por exemplo, SSL/TLS, muitas VPNs, etc.).^[42]

Algoritmos de chave pública são mais frequentemente baseados na complexidade computacional de problemas "difíceis", frequentemente da teoria dos números. Por exemplo, a dificuldade do de RSA está relacionada ao problema de fatoração de inteiros, enquanto a do de Diffie e Hellman e a do DSA estão relacionadas ao problema do logaritmo discreto. A segurança da criptografia de curva elíptica é baseada em problemas teóricos de números envolvendo curvas elípticas. Devido à dificuldade dos problemas subjacentes, a maioria dos algoritmos de chave pública envolve operações como multiplicação modular e exponenciação, que são muito mais caras computacionalmente do que as técnicas usadas na maioria das cifras de bloco, especialmente com tamanhos de chave típicos. Como resultado, os criptossistemas de chave pública são comumente sistemas de criptografia híbridos, nos quais um algoritmo de criptografia de chave simétrica rápido e de alta qualidade é usado para a mensagem em si, enquanto a chave simétrica relevante é enviada com a mensagem, mas criptografada usando um algoritmo de chave pública. Da mesma forma, esquemas de assinatura híbrida são frequentemente usados, nos quais uma função hash criptográfica é computada e apenas o hash resultante é assinado digitalmente.^[5]

As funções de hash criptográficas são funções que recebem uma entrada de comprimento variável e retornam uma saída de comprimento fixo, que pode ser usada, por exemplo, em uma assinatura digital. Para que uma função de hash seja segura, deve ser difícil calcular duas entradas que fazem hash para o mesmo valor (resistência à colisão) e calcular uma entrada que faz hash para uma determinada saída (resistência à pré-imagem). O MD4 é uma função de hash usada há muito tempo que agora está quebrada; o MD5, uma variante reforçada do MD4, também é amplamente usada, mas quebrada na prática. A Agência de Segurança Nacional dos EUA desenvolveu a série Algoritmo de Hash Seguro (SHA) de funções de hash semelhantes ao MD5: O SHA-0 era um algoritmo falho que a agência retirou; o SHA-1 é amplamente implantado e mais seguro que o MD5, mas analistas de criptografia identificaram ataques contra ele; a família SHA-2 melhora o SHA-1, mas é vulnerável a conflitos desde de 2011; e a autoridade de padrões dos EUA achou "prudente" de uma perspectiva de segurança desenvolver um novo padrão para "melhorar significativamente a robustez do kit de ferramentas de algoritmo de hash geral do NIST."^[45] Assim, uma competição de design de função de hash foi criada para selecionar um novo padrão nacional dos EUA, a ser chamado de SHA-3, até 2012. A competição terminou em 2 de outubro de 2012, quando o NIST anunciou que Keccak seria o novo algoritmo de hash SHA-3.^[46] Ao contrário das cifras de bloco e fluxo que são invertíveis, as funções de hash criptográficas produzem uma saída com hash que não pode ser usada para recuperar os dados de entrada originais. As funções de hash criptográficas são usadas para verificar a autenticidade dos dados recuperados de uma fonte não confiável ou para adicionar uma camada de segurança.

Ver artigo principal: Criptoanálise

O objetivo da criptoanálise é encontrar alguma fraqueza ou insegurança em um esquema criptográfico, permitindo assim sua subversão ou evasão.

É um equívoco comum afirmar que todo método de criptografia pode ser quebrado. Em conexão com seu trabalho na Segunda Guerra Mundial na Bell Labs, Claude Shannon provou que a cifra de uso único (OTP) é inquebrável, desde que o material da chave seja verdadeiramente aleatório, nunca reutilizado, mantido em segredo de todos os possíveis invasores e de comprimento igual ou maior que a mensagem.^[55] A maioria das cifras, além das de uso único (OTP), pode ser quebrada com esforço computacional suficiente por ataque de força bruta, mas a quantidade de esforço necessária pode ser exponencialmente dependente do tamanho da chave, em comparação com o esforço necessário para fazer uso da cifra. Em tais casos, a segurança efetiva pode ser alcançada se for provado que o esforço necessário (ou seja, "fator de trabalho", nos termos de Shannon) está além da capacidade de qualquer adversário. Isso significa que deve ser demonstrado que nenhum método eficiente (ao contrário do método de força bruta demorado) pode ser encontrado para quebrar a cifra. Como nenhuma prova desse tipo foi encontrada até o momento, a cifra de uso único (OTP) continua sendo a única cifra teoricamente inquebrável. Embora a criptografia de cifra de uso único (OTP) bem implementada não possa ser quebrada, a análise de tráfego ainda é possível.

Há uma grande variedade de ataques criptoanalíticos, e eles podem ser classificados de várias maneiras. Uma distinção comum depende do que Eve (um invasor) sabe e quais recursos estão disponíveis. Em um ataque somente de texto cifrado, Eve tem acesso somente ao texto cifrado (bons criptossistemas modernos são geralmente efetivamente imunes a ataques somente de texto cifrado). Em um ataque de texto simples conhecido, Eve tem acesso a um texto cifrado e seu texto simples correspondente (ou a muitos pares). Em um ataque de texto simples escolhido, Eve pode escolher um texto simples e aprender seu texto cifrado correspondente (talvez muitas vezes); um exemplo é a jardinagem, usada pelos britânicos durante a Segunda Guerra Mundial. Em um ataque de texto cifrado escolhido, Eve pode ser capaz de escolher textos cifrados e aprender seus textos simples correspondentes.^[5] Finalmente, em um ataque de homem no meio , Eve fica entre Alice (o remetente) e Bob (o destinatário), acessa e modifica o tráfego e então o encaminha para o destinatário.^[56] Também são importantes, e muitas vezes extremamente importantes, os erros (geralmente no design ou no uso de um dos protocolos envolvidos).

A criptoanálise de cifras de chave simétrica normalmente envolve procurar ataques contra as cifras de bloco ou as cifras de fluxo que são mais eficientes do que qualquer ataque que poderia ser contra uma cifra perfeita. Por exemplo, um ataque de força bruta simples contra DES requer um texto simples conhecido e 2⁵⁵ decifragens, tentando aproximadamente metade das chaves possíveis, para atingir um ponto em que as chances são melhores do que até mesmo a chave procurada ter sido encontrada. Mas isso pode não ser garantia suficiente; um ataque de criptoanálise linear contra DES requer 2⁴³ textos simples conhecidos (com seus textos cifrados correspondentes) e aproximadamente 2⁴³ operações DES.^[57] Esta é uma melhoria considerável em relação aos ataques de força bruta.

Algoritmos de chave pública são baseados na dificuldade computacional de vários problemas. Os mais famosos deles são a dificuldade de fatoração de inteiros de semiprimos e a dificuldade de calcular logaritmos discretos, ambos ainda não foram provados como solucionáveis ​​em tempo polinomial (P) usando apenas um computador de completude de Turing clássico. Muita criptoanálise de chave pública diz respeito à criação de algoritmos em P que podem resolver esses problemas, ou usar outras tecnologias, como computadores quânticos. Por exemplo, os algoritmos mais conhecidos para resolver a versão baseada em curva elíptica do logaritmo discreto consomem muito mais tempo do que os algoritmos mais conhecidos para fatoração, pelo menos para problemas de tamanho mais ou menos equivalente. Assim, para atingir uma força equivalente de cifragem, técnicas que dependem da dificuldade de fatorar grandes números compostos, como o sistema de criptografia de RSA, exigem chaves maiores do que técnicas de curva elíptica. Por esse motivo, sistemas de criptografia de chave pública baseados em curvas elípticas se tornaram populares desde sua invenção em meados da década de 1990.

Enquanto a criptoanálise pura usa fraquezas nos próprios algoritmos, outros ataques a sistemas de criptografia são baseados no uso real dos algoritmos em dispositivos reais e são chamados de ataques de canal lateral. Se um criptoanalista tiver acesso, por exemplo, à quantidade de tempo que o dispositivo levou para criptografar uma série de textos simples ou relatar um erro em uma senha ou caractere de PIN, ele pode usar um ataque de tempo para quebrar uma cifra que de outra forma seria resistente à análise. Um invasor também pode estudar o padrão e o comprimento das mensagens para derivar informações valiosas; isso é conhecido como análise de tráfego^[58] e pode ser bastante útil para um adversário alerta. A má administração de um sistema de criptografia, como permitir chaves muito curtas, tornará qualquer sistema vulnerável, independentemente de outras virtudes. Engenharia social e outros ataques contra humanos (por exemplo, suborno, extorsão, chantagem, espionagem, criptoanálise de mangueira de borracha ou tortura) são geralmente empregados devido a serem mais econômicos e viáveis ​​de serem realizados em um período de tempo razoável em comparação com a criptoanálise pura por uma margem alta.

Grande parte do trabalho teórico em criptografia diz respeito a primitivas criptográficas — algoritmos com propriedades criptográficas básicas — e sua relação com outros problemas criptográficos. Ferramentas criptográficas mais complicadas são então construídas a partir dessas primitivas básicas. Essas primitivas fornecem propriedades fundamentais, que são usadas para desenvolver ferramentas mais complexas chamadas sistemas criptográficos ou protocolos criptográficos, que garantem uma ou mais propriedades de segurança de alto nível. Observe, no entanto, que a distinção entre primitivas criptográficas e sistemas criptográficos é bastante arbitrária; por exemplo, o algoritmo de RSA às vezes é considerado um sistema criptográfico e às vezes uma primitiva. Exemplos típicos de primitivas criptográficas incluem funções pseudoaleatórias, funções unidirecionais, etc.

Uma ou mais primitivas criptográficas são frequentemente usadas ​​para desenvolver um algoritmo mais complexo, chamado de sistema criptográfico, ou criptossistema. Os sistemas criptográficos (por exemplo, a cifragem de El-Gamal) são projetados para fornecer funcionalidade particular (por exemplo, cifragem de chave pública) enquanto garantem certas propriedades de segurança (por exemplo, segurança de ataque de texto simples escolhido (CPA) no modelo de oráculo aleatório). Os sistemas criptográficos usam as propriedades das primitivas criptográficas subjacentes para dar suporte às propriedades de segurança do sistema. Como a distinção entre primitivas e sistemas criptográficos é um tanto arbitrária, um sistema criptográfico sofisticado pode ser derivado de uma combinação de vários sistemas criptográficos mais primitivos. Em muitos casos, a estrutura do sistema criptográfico envolve comunicação de ida e volta entre duas ou mais partes no espaço (por exemplo, entre o remetente de uma mensagem segura e seu destinatário) ou ao longo do tempo (por exemplo, dados de backups protegidos criptograficamente). Esses sistemas criptográficos são às vezes chamados de protocolos criptográficos.

Alguns sistemas criptográficos amplamente conhecidos incluem o de RSA, a assinatura de Schnorr, a cifragem de ElGamal e a Privacidade Muito Boa (PGP). Sistemas criptográficos mais complexos incluem sistemas de dinheiro eletrônico,^[59] sistemas de criptografia e assinatura, etc. Alguns sistemas criptográficos mais "teóricos" incluem sistemas de prova interativa,^[60] (como provas de conhecimento zero)^[61] e sistemas para compartilhamento de segredos.^[62][63]

Criptografia leve (LWC) diz respeito a algoritmos de criptografia desenvolvidos para um ambiente estritamente restrito. O crescimento da Internet das Coisas (IoT) impulsionou a pesquisa sobre o desenvolvimento de algoritmos leves que são mais adequados para o ambiente. Um ambiente de IoT requer restrições rígidas sobre consumo de energia, poder de processamento e segurança.^[64] Algoritmos como PRESENT, AES e SPECK são exemplos dos muitos algoritmos LWC que foram desenvolvidos para atingir o padrão definido pelo Instituto Nacional de Padrões e Tecnologia (NIST).^[65]

A criptografia é amplamente usada na Internet para ajudar a proteger os dados de usuários e evitar espionagem. Para garantir o sigilo durante a transmissão, muitos sistemas usam criptografia de chave privada para proteger as informações transmitidas. Com sistemas de chave pública, pode-se manter o sigilo sem uma chave mestra ou um grande número de chaves.^[66] Mas, alguns algoritmos como o BitLocker e o VeraCrypt geralmente não são criptografia de chaves pública e privada. Por exemplo, o Veracrypt usa um hash de senha para gerar a chave privada somente. No entanto, ele pode ser configurado para ser executado em sistemas de chaves públicas e privadas. A biblioteca de cifragem de código aberto OpenSSL em C++ fornece software e ferramentas de cifragem livres e de código aberto. O conjunto de cifras de cifragem mais comumente usado é o AES,^[67] pois tem aceleração de hardware para todos os processadores baseados em x86 que têm AES-NI. Um concorrente próximo é o ChaCha20-Poly1305, que é uma cifra de fluxo, no entanto, é comumente usada para dispositivos móveis, pois são baseados em ARM, que não apresentam extensão de conjunto de instruções AES-NI.

A criptografia pode ser usada para proteger as comunicações cifrando-as. Os sites usam cifragem via HTTPS.^[68] A cifragem "de ponta a ponta", onde apenas o remetente e o destinatário podem ler as mensagens, é implementada para e-mail em Privacidade Muito Boa (PGP) e para mensagens seguras em geral no WhatsApp, Signal e Telegram.^[68]

Os sistemas operacionais usam cifragem para manter as senhas em segredo, ocultar partes do sistema e garantir que as atualizações de software sejam realmente do fabricante do sistema.^[68] Em vez de armazenar senhas em texto simples, os sistemas de computador armazenam hashes delas; então, quando um usuário faz login, o sistema passa a senha fornecida por uma função de hash criptográfica e a compara com o valor com hash no arquivo. Dessa maneira, nem o sistema nem um invasor têm acesso à senha em texto simples.^[68]

A criptografia às vezes é usada para cifrar uma unidade toda. Por exemplo, a Faculdade Universitária de Londres implementou o BitLocker (um programa da Microsoft) para tornar os dados da unidade opacos sem que os usuários façam login.^[68]

Técnicas criptográficas permitem tecnologias de criptomoeda, como tecnologias de razão distribuída (por exemplo, blockchains), que financiam aplicações de criptoeconomia, como finanças descentralizadas (DeFi). Técnicas criptográficas essenciais que permitem criptomoedas e criptoeconomia incluem, mas não estão limitadas a: chaves criptográficas, função de hash criptográfica, cifragem assimétrica (chave pública), autenticação multifatorial (MFA), cifragem ponta a ponta (E2EE) e provas de conhecimento zero (ZKP).

A criptografia tem sido de interesse para agências de coleta de inteligência e de aplicação da lei.^[9] Comunicações secretas podem ser criminosas ou até mesmo traidoras. Devido à sua facilitação de privacidade e à diminuição de privacidade associada à sua proibição, a criptografia também é de interesse considerável para os defensores dos direitos civis. Consequentemente, há um histórico de questões legais controversas em torno da criptografia, especialmente desde que o advento de computadores baratos tornou possível o acesso generalizado à criptografia de alta qualidade.

Em alguns países, até mesmo o uso doméstico da criptografia é, ou foi, restrito. Até 1999, a França restringia significativamente o uso de criptografia internamente, embora tenha relaxado muitas dessas regras desde então. Na China e no Irã, uma licença ainda é necessária para usar criptografia.^[7] Muitos países têm restrições rígidas ao uso da criptografia. Entre as mais restritivas estão as leis da Bielorrússia, Cazaquistão, Mongólia, Paquistão, Cingapura, Tunísia e Vietnã.^[69]

Nos Estados Unidos, a criptografia é legal para uso doméstico, mas tem havido muito conflito sobre questões legais relacionadas à criptografia.^[9] Uma questão particularmente importante tem sido a exportação de criptografia e software e hardware criptográficos. Provavelmente devido à importância da criptoanálise na Segunda Guerra Mundial e à expectativa de que a criptografia continuaria a ser importante para a segurança nacional, muitos governos ocidentais, em algum momento, regulamentaram estritamente a exportação de criptografia. Após a Segunda Guerra Mundial, era ilegal nos EUA vender ou distribuir tecnologia de criptografia no exterior; na verdade, a criptografia foi designada como equipamento militar auxiliar e colocada na Lista de Munições dos Estados Unidos (USML).^[70] Até o desenvolvimento do computador pessoal, algoritmos de chave assimétrica (ou seja, técnicas de chave pública) e da Internet, isso não era especialmente problemático. No entanto, à medida que a Internet cresceu e os computadores se tornaram mais amplamente disponíveis, técnicas de criptografia de alta qualidade se tornaram bem conhecidas em todo o mundo.

Na década de 1990, houve vários desafios à regulamentação de exportação de criptografia dos EUA. Depois que o código-fonte do programa de criptografia Privacidade Muito Boa (PGP) de Philip Zimmermann chegou à Internet em junho de 1991, uma reclamação da RSA Security (então chamada RSA Data Security, Inc.) resultou em uma longa investigação criminal de Zimmermann pelo Serviço de Alfândega dos EUA e pelo FBI, embora nenhuma acusação tenha sido registrada.^[71][72] Daniel J. Bernstein, então um estudante de pós-graduação na UC Berkeley, entrou com uma ação judicial contra o governo dos EUA contestando alguns aspectos das restrições com base em fundamentos de liberdade de expressão. O caso de 1995, Bernstein versus Estados Unidos, resultou em uma decisão de 1999 de que o código-fonte impresso para algoritmos e sistemas criptográficos era protegido como liberdade de expressão pela Constituição dos Estados Unidos.^[73]

Em 1996, trinta e nove países assinaram o Acordo de Wassenaar, um tratado de controle de armas que lida com a exportação de armas e tecnologias de "uso duplo", como criptografia. O tratado estipulou que o uso de criptografia com comprimentos de chave curtos (56 bits para criptografia simétrica, 512 bits para de RSA) não seria mais controlado para exportação.^[74] As exportações de criptografia dos EUA se tornaram menos estritamente regulamentadas como consequência de um grande relaxamento em 2000;^[75] não há mais muitas restrições sobre tamanhos de chave em software de mercado de massa exportado dos EUA. Desde esse relaxamento nas restrições de exportação dos EUA, e porque a maioria dos computadores pessoais conectados à Internet incluem navegadores da web de origem dos EUA, como Firefox ou Internet Explorer, quase todos os usuários da Internet em todo o mundo têm acesso potencial à criptografia de qualidade por meio de seus navegadores (por exemplo, via Segurança da Camada de Transporte). Os programas de cliente de e-mail Mozilla Thunderbird e Microsoft Outlook podem transmitir e receber e-mails via TLS e podem enviar e receber e-mails criptografados com S/MIME. Muitos usuários da Internet não percebem que seu software de aplicação básica contém criptossistemas tão extensos. Esses navegadores e programas de e-mail são tão onipresentes que mesmo governos cuja intenção é regular o uso civil de criptografia geralmente não acham prático fazer muito para controlar a distribuição ou o uso de criptografia dessa qualidade, então, mesmo quando tais leis estão em vigor, a aplicação real é frequentemente efetivamente impossível.

Outra questão controversa relacionada à criptografia nos Estados Unidos é a influência da Agência de Segurança Nacional (NSA) no desenvolvimento e na política de cifras.^[9] A NSA esteve envolvida com o design do DES durante seu desenvolvimento na IBM e sua consideração pelo Escritório Nacional de Padrões como um possível Padrão Federal para criptografia.^[76] O DES foi projetado para ser resistente à criptoanálise diferencial,^[77] uma técnica criptoanalítica poderosa e geral conhecida pela NSA e pela IBM, que se tornou publicamente conhecida apenas quando foi redescoberta no final da década de 1980.^[78] De acordo com Steven Levy, a IBM descobriu a criptoanálise diferencial,^[72] mas manteve a técnica em segredo a pedido da NSA. A técnica se tornou publicamente conhecida apenas quando Biham e Shamir a redescobriram e anunciaram alguns anos depois. Todo o caso ilustra a dificuldade de determinar quais recursos e conhecimento um invasor pode realmente ter.

Outro exemplo do envolvimento da NSA foi o caso do chip Clipper de 1993, um microchip de criptografia destinado a fazer parte da iniciativa de controle de criptografia Capstone. O Clipper foi amplamente criticado por criptógrafos por dois motivos. O algoritmo de cifra (chamado Skipjack) foi então classificado (desclassificado em 1998, muito depois que a iniciativa Clipper caducou). A cifra classificada causou preocupações de que a NSA havia deliberadamente tornado a cifra fraca para auxiliar seus esforços de inteligência. Toda a iniciativa também foi criticada com base em sua violação do Princípio de Kerckhoffs, pois o esquema incluía uma chave de custódia especial mantida pelo governo para uso pela aplicação da lei (ou seja, grampo telefônico).^[72]

Ver artigo principal: Gestão de direitos digitais

A criptografia é central para o gerenciamento de direitos digitais (DRM), um grupo de técnicas para controlar tecnologicamente o uso de material protegido por direitos autorais, sendo amplamente implementado e implantado a pedido de alguns detentores de direitos autorais. Em 1998, o presidente dos EUA Bill Clinton assinou a Lei de Direitos Autorais do Milênio Digital (DMCA), que criminalizou toda a produção, disseminação e uso de certas técnicas e tecnologias criptoanalíticas (agora conhecidas ou descobertas posteriormente); especificamente, aquelas que poderiam ser usadas para contornar esquemas tecnológicos de DRM.^[79] Isso teve um impacto notável na comunidade de pesquisa em criptografia, pois pode-se argumentar que qualquer pesquisa criptoanalítica violava o DMCA. Estatutos semelhantes foram promulgados em vários países e regiões, incluindo a implementação na Diretiva de Direitos Autorais da UE. Restrições semelhantes são exigidas por tratados assinados por estados-membros da Organização Mundial da Propriedade Intelectual.

O Departamento de Justiça dos Estados Unidos e o FBI não aplicaram a DMCA tão rigorosamente quanto alguns temiam, mas a lei, no entanto, continua sendo controversa. Niels Ferguson, um respeitado pesquisador de criptografia, declarou publicamente que não divulgará parte de sua pesquisa sobre um projeto de segurança da Intel por medo de processo sob a DMCA.^[80] O criptologista Bruce Schneier argumentou que a DMCA incentiva o bloqueio do fornecedor, ao mesmo tempo em que inibe medidas reais em direção à segurança cibernética.^[81] Tanto Alan Cox (desenvolvedor do núcleo Linux de longa data) quanto Edward Felten (e alguns de seus alunos em Princeton) encontraram problemas relacionados à Lei. Dmitry Sklyarov foi preso durante uma visita aos EUA da Rússia e preso por cinco meses, aguardando julgamento por supostas violações da DMCA decorrentes do trabalho que ele havia feito na Rússia, onde o trabalho era legal. Em 2007, as chaves criptográficas responsáveis ​​pela codificação de conteúdo de Blu-ray e HD DVD foram descobertas e lançadas na Internet. Em ambos os casos, a Associação Cinematográfica da América (MPAA) enviou inúmeras notificações de remoção da DMCA, e houve uma reação massiva na Internet^[10] desencadeada pelo impacto percebido de tais notificações no uso justo e na liberdade de expressão.

No Reino Unido, a Lei de Regulamentação dos Poderes Investigativos dá à polícia do Reino Unido poderes para forçar suspeitos a decifrar arquivos ou entregar senhas que protegem chaves de cifragem. O não cumprimento é uma infração por si só, punível por condenação com uma pena de prisão de dois anos ou até cinco anos em casos envolvendo segurança nacional.^[8] Processos bem-sucedidos ocorreram sob a Lei; o primeiro, em 2009,^[82] resultou em uma pena de 13 meses de prisão.^[83] Leis semelhantes de divulgação forçada na Austrália, Finlândia, França e Índia obrigam suspeitos individuais sob investigação a entregar chaves de cifragem ou senhas durante uma investigação criminal.

Nos Estados Unidos, o caso criminal federal de Estados Unidos versus Fricosu abordou se um mandado de busca pode obrigar uma pessoa a revelar uma senha ou frase-senha de cifragem.^[84] A Fundação Fronteira Eletrônica (EFF) argumentou que isso é uma violação da proteção contra autoincriminação dada pela Quinta Emenda.^[85] Em 2012, o tribunal decidiu que, de acordo com a Lei de Todos os Mandados, o réu era obrigado a apresentar um disco rígido que não estivesse cifrado para o tribunal.^[86]

Em muitas jurisdições, a situação legal da divulgação forçada permanece obscura.

A disputa de cifragem FBI e Apple, de 2016, diz respeito à capacidade dos tribunais nos Estados Unidos de obrigar a assistência dos fabricantes no desbloqueio de celulares cujos conteúdos são protegidos criptograficamente.

Como uma possível contramedida à divulgação forçada, alguns softwares criptográficos suportam a negação plausível, onde os dados cifrados são indistinguíveis de dados aleatórios que não são utilizados (por exemplo, como os de uma unidade que foi apagada com segurança).

• Chave pré-compartilhada – Método para definir chaves de cifragem
• Criptovirologia – Virologia de cifragem e segurança
• Guerras criptográficas – Tentativas de limitar o acesso à criptografia forte
• Vigilância global – Vigilância em massa através das fronteiras nacionais
• Teoria da informação – Estudo científico da informação digital

• Wykes, Sean Michael (2016). Criptografia Essencial - a Jornada do Criptógrafo. Brasil: Elsevier. ISBN 978-85-352-8605-2 
• Hook, David (2005). Beginning Cryptography with Java (em inglês). Indianapolis: Wrox. 448 páginas. ISBN 0-7645-9633-0 
• PELLEGRINI, Jerônimo C. Introdução à Criptografia e seus Fundamentos : notas de aula : versão 90.
• QUARESMA, Pedro; LOPES, Elsa. Criptografia.
• Schneier, Bruce (1996). Applied Cryptography (em inglês). New York: John Wiley and Sons. 758 páginas. ISBN 0-471-11709-9 
• SINGH, Simon. O Livro dos Códigos. Lisboa : Temas e Debates, 2001. ISBN 972-759-278-3.

• Media relacionados com Criptografia no Wikimedia Commons
• Mais sobre criptografia
• Criptografia com números irracionais

• Portal das tecnologias de informação