Curva de fase

Em astronomia, uma curva de fase descreve o brilho de um corpo refletor como uma função do seu ângulo de fase. O brilho normalmente é referido à magnitude absoluta do objeto, que, por sua vez, é a magnitude aparente à distância de uma unidade astronômica da Terra e do Sol. O ângulo de fase é igual ao arco subtendido pelo observador e o Sol, medido no objeto.

A curva de fase é útil para caracterizar o regolito (solo) e a atmosfera do objeto celeste. Ela também é a base para calcular o albedo geométrico e o albedo de Bond do objeto. Na geração de efeméride, a curva de fase é utilizada em conjunto com as distâncias do objeto para o Sol e a Terra para calcular a magnitude aparente.

Mercúrio

[editar | editar código-fonte]
A curva de fase de Mercúrio e seu efeito da oposição.[1]

A curva de fase de Mercúrio é muito íngreme, o que é característico de um corpo cujo regolito está exposto à visão. Em ângulos de fase maiores que 90° (fase crescente), o brilho decresce de forma especialmente brusca. A forma da curva de fase indica uma inclinação média na superfície de Mercúrio de aproximadamente 16°,[1] o que é ligeiramente mais suave do que a da Lua. Ao se aproximar do ângulo de fase 0° (fase totalmente iluminada), a curva sobe para um pico agudo. Este aumento repentino do brilho é chamado efeito da oposição,[2][3] porque para a maioria dos corpos (embora não para Mercúrio) ele ocorre na oposição astronômica, quando o corpo está oposto ao Sol no céu. A largura do crescimento de oposição para Mercúrio indica que tanto o estado de compactação do regolito quanto a distribuição de tamanhos de partículas no planeta são semelhantes aos da Lua.[1]

As primeiras observações visuais que contribuíram para a curva de fase de Mercúrio foram realizadas por G. Muller[4] nos anos 1800 e por André-Louis Danjon[5][6][7] na metade do século XX. W. Irvine e colegas[8] utilizaram fotometria fotoelétrica nos anos 1960. Alguns desses dados iniciais foram analisados por G. de Vaucouleurs,[9][10] sumarizados por D. Harris[11] e utilizados para predizer magnitudes aparentes no Almanaque Astronômico[12] por várias décadas. Novas observações altamente acuradas, cobrindo a mais ampla faixa de ângulos de fase até o momento (de 2° a 170°), foram realizadas por A. Mallama, D. Wang e R. Howard,[1] usando o instrumento Large Angle and Spectrometric Coronograph (LASCO) e o satélite Solar and Heliospheric Observatory (SOHO) da Agência Espacial Europeia e da NASA. Eles também fizeram novas observações com CCD a partir do solo. Esses dados são, atualmente, a mais importante fonte para a curva de fase usada no Almanaque Astronômico[13] para predizer magnitudes aparentes.

O brilho aparente de Mercúrio visto da Terra é maior no ângulo de fase 0° (conjunção superior com o Sol), quando ele pode atingir a magnitude -2,6.[14] Em ângulos de fase próximos a 180° (conjunção inferior), o planeta perde brilho até a magnitude +5,[14] sendo que o brilho exato depende do ângulo de fase naquela conjunção específica. Esta diferença de mais de 7 magnitudes corresponde a uma variação de mais de mil vezes no brilho aparente.

Vênus

[editar | editar código-fonte]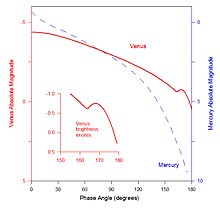
A curva de fase de Vênus[15] comparada à de Mercúrio[1] e o excesso de brilho de Vênus.

A curva de fase relativamente plana de Vênus é característica de um planeta enevoado.[14] Em contraste com Mercúrio, cuja curva apresenta um pico forte ao se aproximar do ângulo de fase 0° (fase cheia), a de Vênus é arredondada. O largo ângulo de espalhamento da iluminação pelas nuvens, em comparação com o espalhamento mais estreito pelo regolito, causa este achatamento da curva de fase. Vênus apresenta um aumento de brilho perto do ângulo de fase 170°, quando está num crescente fino, devido ao espalhamento da luz solar por gotículas de ácido sulfúrico que estão acima do topo das nuvens do planeta.[15] Mesmo além dos 170° o brilho não decresce muito bruscamente.

A história da observação e análise da curva de fase de Vênus é similar à de Mercúrio. O melhor conjunto de observações e interpretações modernas foi reportado por A. Mallama, D. Wang e R. Howard.[15] Eles utilizaram o instrumento LASCO na sonda SOHO e equipamentos de CCD em solo para observar a curva de fase de 2° até 179°. Como com Mercúrio, esses novos dados são a principal fonte da curva de fase usada no Almanaque Astronômico[13] para predizer magnitudes aparentes.

Em contraste com Mercúrio, o brilho aparente máximo de Vênus visto da Terra não ocorre no ângulo de fase 0°. Como a curva de fase de Vênus é relativamente plana, enquanto sua distância para a Terra varia bastante, o brilho máximo ocorre quando o planeta está em crescente, no ângulo de fase 125°, quando o brilho de Vênus pode chegar à magnitude -4,9.[14] Próximo da conjunção inferior, o planeta tipicamente perde brilho até a magnitude -3,[14] embora o valor exato dependa do ângulo de fase. A variação típica do brilho aparente de Vênus no curso de uma aparição é menos do que um fator de 10, ou apenas 1% da de Mercúrio.

Terra

[editar | editar código-fonte]

A curva de fase da Terra não foi determinada tão precisamente quanto as de Mercúrio e Vênus, porque o seu brilho integrado é difícil de medir a partir da superfície. Em lugar da observação direta, o brilho da Terra refletido na porção da Lua não iluminada pelo Sol serviu como substituto. Algumas medições diretas da luminosidade da Terra foram obtidas com a sonda EPOXI. Apesar de elas não cobrirem muito da curva de fase, elas revelam uma curva de luz rotacional causada pelo trânsito de oceanos escuros e massas de terra brilhantes através do hemisfério. P Goode e colegas no Observatório Solar Big Bear, na Califórnia, mediram o brilho da Terra[16] e T. Livengood da NASA analisou os dados da EPOXI.[17]

A Terra vista de Vênus, próxima da oposição do Sol, é extremamente brilhante, com magnitude -6. Para um observador em Marte nosso planeta apareceria mais luminoso perto do momento de máxima elongação do Sol, com magnitude aproximada de -1,5.

Marte

[editar | editar código-fonte]
A curva de fase de Marte[18] comparada à de Mercúrio.[1]

Apenas aproximadamente 50° da curva de fase de Marte podem ser observados da Terra, porque sua órbita é mais distante do Sol que a do nosso planeta. Há um efeito da oposição, mas ele é menos pronunciado que o de Mercúrio. A rotação de pontos da superfície brilhantes e escuros ao longo do seu disco e variações do estado de sua atmosfera (inclusive suas tempestades de poeira) provocam variações na curva de fase. R. Schmude[19][20] obteve muitas das medições de brilho usadas em uma abrangente análise da curva de fase realizada por A. Mallama.[18]

Como a órbita de Marte é consideravelmente excêntrica, seu brilho na oposição pode variar entre as magnitudes -3,0 e -1,4.[14] O brilho mínimo é aproximadamente magnitude +1,6,[14] quando Marte está no lado oposto do Sol em relação à Terra. Variações rotacionais podem aumentar ou reduzir o brilho de Marte em 5%, e tempestades de poeira globais podem aumentar sua luminosidade em 25%.[14][18]

Gigantes gasosos

[editar | editar código-fonte]

Os planetas mais externos (Júpiter (planeta)|Júpiter]], Saturno, Urano e Netuno) estão tão distantes que apenas pequenas porções de suas curvas de fase próximas a 0° (fase cheia) podem ser avaliadas da Terra. Esta parte da curva para esses planetas enevoados é, geralmente, razoavelmente plana, como a de Vênus.

A magnitude aparente de Júpiter varia de -2,9 a -1,4, a de Saturno de -0,5 a +1,4, a de Urano de +5,3 a +6,0 e a de Netuno de +7,8 a +8,0. Muitas dessas variações se devem à distância. Entretanto, a variação de magnitude de Saturno também depende do seu sistema de anéis, conforme explicado abaixo.

Os anéis de Saturno

[editar | editar código-fonte]
A curva de fase de Saturno, conforme Schmude,[21] demonstrando o efeito da oposição do sistema de anéis.

O brilho do sistema Saturno depende da orientação do seu sistema de anéis. Os anéis contribuem mais para o brilho global do sistema quando eles estão mais inclinados para a direção da iluminação do Sol e para a visão do observador. Anéis bem abertos contribuem com 1 magnitude em comparação ao brilho somente do disco.[14] As partículas geladas que compõem os anéis também produzem um forte aumento de oposição. Imagens do Telescópio Espacial Hubble e da nave Cassini foram analisadas numa tentativa de caracterizar as partículas do anel com base em suas curvas de fase.[22][23][24][25]

Lua

[editar | editar código-fonte]
A curva de fase da Lua,[26] comparada com a de Mercúrio.[1]

A curva de fase da Lua se parece com a de Mercúrio devido às similaridades das superfícies e à falta de uma atmosfera em ambos os corpos.[27] Os dados da sonda Clementine, analisados por J. Hillier, B. Buratti e K. Hill,[28] indicam um aumento de oposição. A magnitude aparente da Lua na fase cheia é -12,7,[29] enquanto na fase quarto tem menos de 10% deste brilho.[26]

Satélites planetários

[editar | editar código-fonte]

As curvas de fase de muitos satélites naturais de outros planetas[30][31] foram observadas e interpretadas. Os satélites gelados frequentemente exibem aumentos de brilho na oposição. Este comportamento foi usado para modelar suas superfícies.

Asteroides

[editar | editar código-fonte]

As curvas de fase de muitos asteroides[32] foram observadas e eles também exibem aumentos da oposição. Os asteroides podem ser classificados fisicamente desta forma.[33] Os efeitos da rotação podem ser muito grandes e têm que ser segregados antes de a curva de fase ser calculada. Um exemplo de tal estudo foi reportado por R. Baker e colegas.[34]

Exoplanetas

[editar | editar código-fonte]

Programas para caracterizar planetas fora do Sistema Solar dependem fortemente da espectroscopia para identificar constituintes e estados da atmosfera, especialmente aqueles que apontam para a presença de formas de vida ou que poderiam suportar a vida. Entretanto, o brilho pode ser medido para objetos do tamanho da Terra muito distantes, que são muito tênues para análise espectroscópica. A. Mallama[35] demonstrou que a análise da curva de fase pode ser uma ferramenta útil para identificar planetas que são similares à Terra. Além disso, J. Bailey[36] indicou que anomalias da curva de fase, como o excesso de brilho de Vênus, podem ser indicadores úteis de constituintes atmosféricos como a água, que podem ser essenciais para a vida no universo.

Críticas à modelagem pela curva de fase

[editar | editar código-fonte]

Inferências sobre regolitos a partir de curvas de fase são frequentemente baseadas na parametrização Hapke. Entretanto, num teste cego, M. Shepard e P. Helfestein[37] não encontraram forte evidência de que um conjunto particular de parâmetros Hapke derivados de dados fotométricos poderiam revelar singularmente o estado físico de amostras de laboratório. Esses testes incluíram a modelagem das funções de fase de três termos de Henyey-Greenstein e o efeito da oposição de retroespalhamento coerente. Este achado negativo sugere que o modelo de transferência de radiação desenvolvido por B. Hapke pode ser inadequado para a modelagem física baseada em fotometria.

Referências

  1. ↑ a b c d e f g Mallama, A.; Wang, D.; Howard, R.A. (2002). «Photometry of Mercury from SOHO/LASCO and Earth». Icarus. 155 (2): 253–264. Bibcode:2002Icar..155..253M. doi:10.1006/icar.2001.6723 
  2. ↑ Shkuratov, Y. G., M. A. Kreslavsky, A. A. Ovcharenko, D. G. Stankevich, and E. S. Zubko (1999). «Opposition Effect from Clementine Data and Mechanisms of Backscatter». Icarus. 141: 132–155. Bibcode:1999Icar..141..132S. doi:10.1006/icar.1999.6154 
  3. ↑ Helfenstein, P., Veverka, J., and Hillier, J. (1997). «The lunar opposition effect: A test of alternative models». Icarus. 128: 2–14. Bibcode:1997Icar..128....2H. doi:10.1006/icar.1997.5726 
  4. ↑ Muller, G. (1893). «Helligkeitsbestimmungen der grossen planeten und einiger asteroiden». Publ. Astrophys. Obs. Potsdam. 8 (92): 197–398 
  5. ↑ Danjon, A. (1949). «Photometrie et colorimetrie des planetes Mercure et Venus». Bull. Astron. 14: 315–345 
  6. ↑ Danjon, A. (1950). «Correction to Danjon 1949». Bull. Astron. 14. 315 páginas 
  7. ↑ Danjon, A. (1953). «Correction to Danjon 1949». Bull. Astron. 17. 363 páginas 
  8. ↑ Irvine, W. H., T. Simon, D. H. Menzel, C. Pikoos, and A. T. Young (1968). «Multicolor photoelectric photometry of the brighter planets III». Astron. J. 73: 807–828. Bibcode:1968AJ.....73..807I. doi:10.1086/110702 
  9. ↑ de Vaucouleurs, G. (1964). «Geometric and photometric parameters of the terrestrial planets». Icarus. 3 (3): 187–235. Bibcode:1964Icar....3..187D. doi:10.1016/0019-1035(64)90018-1 
  10. ↑ deVaucouleurs, G. (1970). A. Dollfus, ed. in Surface and Interiors of the Planets and Satellites. [S.l.]: Academic Press. p. 225 
  11. ↑ Harris, D.L. (1961). G.P. Kuiper & B.A. Middlehurst, ed. in Planets and Satellites. [S.l.]: U. Chicago Press. p. 272 
  12. ↑ Hilton, J.L. (1992). P.K. Seidelmann, ed. in Explanatory Supplement to the Astronomical Almanac. [S.l.]: University Science Books. p. 383 
  13. ↑ a b Hilton, J.L. (2005). «Improving the visual magnitudes of the planets in the Astronomical Almanac. I. Mercury and Venus». Astron. J. 129 (6): 2902–2906. Bibcode:2005AJ....129.2902H. doi:10.1086/430212 
  14. ↑ a b c d e f g h i Mallama, A. (2011). «Planetary magnitudes». Sky and Telescope. 121 (1): 51–56 
  15. ↑ a b c Mallama, A.; Wang, D.; Howard, R.A. (2006). «Venus phase function and forward scattering from H2SO4». Icarus. 182: 10–22. Bibcode:2006Icar..182...10M. doi:10.1016/j.icarus.2005.12.014 
  16. ↑ Goode, P.R., Qiu, J., Yurchyshyn, V., Hickey, J., Chu, M.C., Kolbe, E., Brown, C.T., and Koonin, S.E. (2001). «Earthshine observations of the Earth's reflectance». Geophys. Res. Lett. 28 (9): 1671–1674. Bibcode:2001GeoRL..28.1671G. doi:10.1029/2000GL012580 
  17. ↑ Livengood, T., and 10 co-authors (2008). «EPOXI empirical test of optical characterization of an Earth-like planet». Bull. Am. Astron. Soc. 40: Presentation 01.03 
  18. ↑ a b c Mallama, A. (2007). «The magnitude and albedo of Mars». Icarus. 192 (2): 404–416. Bibcode:2007Icar..192..404M. doi:10.1016/j.icarus.2007.07.011 
  19. ↑ Schmude , R.W. Jr. (2004). «ALPO observations of the 2003 apparition of Mars». J. Assoc. Lunar Planet. Observ. 46: 28–42 and references therein 
  20. ↑ Schmude, R.W. Jr. (2006). «Wideband photometry of Mars: 1991–2006». Bull. Am. Astron. Soc. 38 (3): 600 and references therein 
  21. ↑ Schmude, R.W. Jr. (2011). «The magnitude and color of the Saturn system». Icarus. 211: 732–739. Bibcode:2011Icar..211..732S. doi:10.1016/j.icarus.2010.09.018 
  22. ↑ French, R.G., Verbiscer, A., Salo, H., McGhee, C., and Dones, L. (2007). «Saturn's rings at true opposition». Pub. Astr. Soc. Pacific. 119 (856): 623–643. Bibcode:2007PASP..119..623F. doi:10.1086/519982 
  23. ↑ Poulet, F., Cuzzi, J. N., French, R.G., Dones, L. (2002). «A study of Saturn's ring phase curves from HST observations». Icarus. 158: 224–248. Bibcode:2002Icar..158..224P. doi:10.1006/icar.2002.6852 
  24. ↑ Cuzzi, J.N., French, R.G., Dones, L. (2002). «HST multicolor (255–1042 nm) photometry of Saturn's main rings». Icarus. 158: 199–223. Bibcode:2002Icar..158..199C. doi:10.1006/icar.2002.6851 
  25. ↑ Salo, H.; French, R. G. (2010). «The opposition and tilt effects of Saturn's rings from HST observations». Icarus. 210 (2): 785–816. Bibcode:2010Icar..210..785S. arXiv:1007.0349Acessível livremente. doi:10.1016/j.icarus.2010.07.002 
  26. ↑ a b Cox, A.N. (2000). Allen's Astrophysical Quantities, fourth edition. [S.l.]: Springer-Verlag. pp. 307–310 
  27. ↑ Warell, J. (2004). «Properties of the Hermean regolith: IV. Photometric parameters of Mercury and the Moon contrasted with Hapke modelling». Icarus. 167 (2): 271–286. Bibcode:2004Icar..167..271W. doi:10.1016/j.icarus.2003.10.010 
  28. ↑ Hillier, J., Buratti B., and Hill, K. (1999). «Multispectral photometry of the Moon and absolute calibration of the Clementine UV/VIS camera». Icarus. 141 (2): 205–225. Bibcode:1999Icar..141..205H. doi:10.1006/icar.1999.6184 
  29. ↑ Williams, Dr. David R. (2 de fevereiro de 2010). «Moon Fact Sheet». NASA (National Space Science Data Center). Consultado em 17 de novembro de 2010 
  30. ↑ Bauer, J.M., Grav, T., Buratti, B.J. and Hicks, M.D. (2006). «The phase curve survey of the irregular saturnian satellites: A possible method of physical classification». Icarus. 184: 181–197. Bibcode:2006Icar..184..181B. doi:10.1016/j.icarus.2006.04.011 
  31. ↑ Deau, E., Dones, L., Rodriguez, S., Charnoz, S. and Brahic, A. (2009). «The opposition effect in the outer Solar system: A comparative study of the phase function morphology». Planetary and Space Science. 57 (11): 1282–1301. Bibcode:2009P&SS...57.1282D. arXiv:0902.0345Acessível livremente. doi:10.1016/j.pss.2009.05.005 
  32. ↑ Cox, A.N. (2000). Allen's Astrophysical Quantities, fourth edition. [S.l.]: Springer-Verlag. p. 299 
  33. ↑ Kaasalainen, S., Piironen, J., Kaasalainen, M., Harris, A.W., Muinonen, K. and Cellino, A. (2003). «Asteroid photometric and polarimetric phase curves: empirical interpretation». Icarus. 161: 34–46. Bibcode:2003Icar..161...34K. doi:10.1016/S0019-1035(02)00020-9 
  34. ↑ Baker, R.E., Benishek, V., Pilcher, F., and Higgins, D.; Benishek; Pilcher; Higgins (2010). «Rotation period and H-G parameters determination for 1700 Zvezdara: A collaborative photometry project» (PDF). The Minor Planet Bulletin. 37 (3): 81–83. Bibcode:2010MPBu...37...81B [ligação inativa]
  35. ↑ Mallama, A. (2009). «Characterization of terrestrial exoplanets based on the phase curves and albedos of Mercury, Venus and Mars». Icarus. 204: 11–14. Bibcode:2009Icar..204...11M. doi:10.1016/j.icarus.2009.07.010 
  36. ↑ Bailey, J. (2007). «Rainbows, polarization, and the search for habitable planets». Astrobiology. 7 (2): 320–332. Bibcode:2007AsBio...7..320B. PMID 17480163. doi:10.1089/ast.2006.0039 
  37. ↑ Shepard, M. K. & Helfenstein, P. (2007). «A test of the Hapke photometric model». J. Geophys. Res. 112: E03001. Bibcode:2007JGRE..11203001S. doi:10.1029/2005JE002625 
Obtida de "https://pt.wikipedia.org/w/index.php?title=Curva_de_fase&oldid=68741139"