Ideal primo

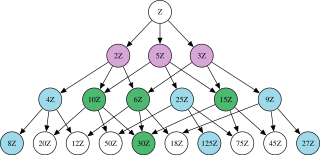
Em álgebra, um ideal primo é um subconjunto de um anel que tem várias propriedades em comum com as de um número primo do anel dos inteiros.^[1][2] Os ideais primos para os inteiros são os conjuntos que contém todos os múltiplos de um número primo dado, juntamente com o ideal nulo.

Ideais primitivos são primos, e ideais primos são tanto primários quanto semiprimos.

Um ideal P de um anel comutativo R é primo se ele possui as duas propriedades a seguir:

• Se a e b são elementos de R tais que o seu produto ab é um elemento de P, então a está em P ou b está em P,
• P é diferente de todo o anel R.

Isto generaliza a seguinte propriedade dos números primos: se p é um número primo e se p divide um produto ab de dois inteiros, então p divide a ou p divide b. Pode-se então dizer que

Um inteiro positivo n é um número primo se e somente se o ideal nZ é um ideal primo de Z.

• Se R denota o anel C[X, Y] dos polinômios em duas variáveis com coeficientes complexos, então o ideal gerado pelo polinômio Y ² − X ³ − X − 1 é um ideal primo (ver curva elíptica).
• No anel Z[X] de todos os polinômios com coeficientes inteiros, o ideal gerado por 2 e X é um ideal primo. Ele consiste de todos os polinômios cujo termo constante é par.
• Em qualquer anel R, um ideal maximal é um ideal M que é maximal no conjunto de todos os ideais próprios de R, isto é, M está contido em exatamente dois ideais de R, a saber, o próprio M e o anel todo R. Na verdade todo ideal maximal é primo. Em um domínio de ideais principais todo ideal primo não nulo é maximal, mas isso não é verdade em geral.
• Se M é uma variedade suave, R é o anel de funções reais suaves sobre M, e x é um ponto de M, então o conjunto de todas as funções suaves f com f (x) = 0 formam um ideal primo (e também um ideal maximal) em R.

• Um ideal I do anel (com unidade) R é primo se e somente se o anel quociente R/I é um domínio de integridade. Em particular, um anel comutativo é um domínio de integridade se e somente se (0) é um ideal primo.
• Um ideal I é primo se e somente se seu complemento é fechado para a multiplicação.^[3]
• Todo anel não nulo contém no mínimo um ideal primo (de fato ele contém pelo menos um ideal maximal), o que é uma consequência direta do teorema de Krull.
• O conjunto de todos os ideais primos (o espectro de um anel) contém elementos minimais (chamados de primos minimais). Geometricamente, eles correspondem às componentes irredutíveis do espectro.
• A preimagem de um ideal primo por um homomorfismo de anéis é um ideal primo.
• A soma de dois ideais primos não é necessariamente um ideal primo. Por exemplo, considere o anel C[x, y] com ideais primos P = (x² + y² − 1) e Q = (x) (os ideais gerados por x² + y² − 1 e x respectivamente). Sua soma P + Q = (x² + y² − 1, x) = (y² − 1, x) no entanto não é um ideal primo: y² − 1 = (y − 1)(y + 1) ∈ P + Q mas seus dois fatores não estão. Alternativamente, note que o anel quociente tem divisores de zero e consequentemente não é um domínio de integridade e assim P + Q não pode ser primo.
• Em um anel comutativo R com pelo menos dois elementos, se todo ideal próprio é primo, então o anel é um corpo. (se o ideal (0) é primo, então o anel R é um domínio de integridade. Se q é qualquer elemento não nulo de R e o ideal (q²) é primo, então ele contém q e então q é invertível.)
• Um ideal principal não nulo é primo se e somente se ele é gerado por um elemento primo. Em um domínio de fatoração única, todo ideal primo não nulo contém um elemento primo.

Um dos uso dos ideais primos é na geometria algébrica, onde variedades são definidas como o conjunto zero de ideais em anéis de polinômios. Acontece que as variedades irredutíveis correspondem a ideais primos. Na abordagem abstrata moderna, começa-se com um anel comutativo arbitrário e transforma-se o conjunto de seus ideais primos, também chamado de seu espectro, em um espaço topológico e pode-se, então, definir generalizações de variedades chamadas de esquemas, que encontram aplicações não só na geometria, mas também na teoria dos números.

A introdução dos ideais primos na teoria algébrica dos números foi um grande avanço: percebeu-se que a importante propriedade da fatoração única expressa no teorema fundamental da aritmética não vale em todo anel de inteiros algébricos, mas foi encontrado um substituto quando Richard Dedekind substituiu elementos por ideais e elementos primos por ideais primos; ver domínio de Dedekind.

A noção de ideal primo pode ser generalizada para anéis não comutativos usando a definição comutativa "por-ideais". Wolfgang Krull avançou esta ideia em 1928.^[4] O conteúdo a seguir pode ser encontrada em textos como (Goodearl 2004) e (Lam, 2001). Se R é um anel (possivelmente comutativo) e P é um ideal em R diferente do próprio R, dizemos que P é primo se para quaisquer dois ideais A e B de R:

• Se o produto de ideais AB está contido em P, então pelo menos um dos ideais A e B está contido em P.

Pode ser mostrado que esta definição é equivalente à comutativa no caso de anéis comutativos. É facilmente verificado que, se um ideal de um anel não comutativo R satisfaz a definição comutativa de primo, então ele também satisfaz a versão não comutativa. Um ideal P satisfazendo a definição comutativa de primo é às vezes chamado de ideal completamente primo para distingui-lo de outros ideais meramente primos no anel. Ideais completamente primos são ideais primos, mas a recíproca não é verdadeira. Por exemplo, o ideal zero no anel das matrizes n × n sobre um corpo é um ideal primo, mas não é completamente prime.

Isto é próximo do ponto de vista histórico de ideais como números ideais, já que para o anel Z "A está contido em P" é outra maneira de dizer "P divide A", e o ideal unidade R representa a unidade.

Formulações equivalentes do ideal P ≠ R ser primo incluem as seguintes propriedades:

• Para quaisquer a e b em R, (a)(b) ⊆ P implica a ∈ P ou b ∈ P.
• Para quaisquer dois ideais à direita de R, AB ⊆ P implica A ⊆ P ou B ⊆ P.
• Para quaisquer dois ideais à esquerda de R, AB ⊆ P implica A ⊆ P ou B ⊆ P.
• Para quaisquer elementos a e b de R, se aRb ⊆ P, então a ∈ P ou b ∈ P.

Ideais primos em anéis comutativos são caracterizados por ter complementos fechados multiplicativamente em R, e com ligeira modificação, pode ser formulada uma caracterização semelhante para ideais primos em anéis não comutativos. Um subconjunto não vazio S ⊆ R é chamado de m-sistema se para quaisquer a e b em S, existe r em R tal que arb está em S.^[5] Pode-se então acrescentar o item a seguir à lista de condições equivalentes acima:

• O complemento R\P é um m-sistema.

• Qualquer ideal primitivo é primo.
• Tal como no caso de anéis comutativos, os ideais maximais são primos, e ideais primos também contém ideais primos minimais.
• Um anel é um anel primo se, e somente se, o ideal zero é um ideal primo, e além disso um anel é um domínio se, e somente se, o ideal zero é um ideal completamente primo.
• Outro fato da teoria comutativa que se repete na teoria não comutativa é que se A é um R módulo diferente de zero, e P é um elemento maximal no poset de ideais anuladores de submódulos de A, então P é primo.

• Lema da evitação dos ideais primos. Se R é um anel comutativo, e A é um subanel (possivelmente sem unidade), e I₁, ..., I_n é uma coleção de ideais de R com, no máximo, dois membros não primos, então se Um não está contido em qualquer I_j, ele também não está contido na união de I₁, ..., I_n.^[6] Em particular, Um poderia ser um ideal de R.
• Se S é qualquer m-sistema em R, então um lema essencialmente devido a Krull mostra que existe um ideal de R maximal em relação a ser disjunto de S, e que além disso deve ser um ideal primo.^[7] No caso em que {S} = {1}, tem-se o teorema de Krull, e este recupera os ideais maximais de R. Outro protótipo de m-sistema é o conjunto {x, x², x³, x⁴, ...}, de todas as potências positivas de elemento não-nilpotente.
• Para um ideal primo P, o complemento R\P tem outra propriedade além de ser um m-sistema. Se xy está em R\P, então tanto x quanto y devem estar em R\P, pois P é um ideal. Um conjunto que contém os divisores de seus elementos é chamado de saturado.
• Para um anel comutativo R, existe uma espécie de recíproca para a afirmação anterior: Se S é qualquer conjunto não vazio de R saturado e fechado multiplicativamente, o complemento R\S é uma união de ideais primos de R.^[8]
• A intersecção dos membros de uma cadeia descendente de ideais primos é um ideal primo, e em um anel comutativo a união dos membros de uma cadeia ascendente de ideais primos é um ideal primo. Com o Lema de Zorn, estas observações implicam que o poset de ideais primos de um anel comutativo (ordenado parcialmente por inclusão) tem elementos maximal e minimal.

Ideais primos frequentemente podem ser produzidos como elementos maximais de determinadas coleções de ideais. Por exemplo:

• Um ideal maximal com respeito a ter intersecção vazia com um m-sistema fixo é primo.
• Um ideal maximal entre os anuladores de submódulos de um R módulo fixo M é primo.
• Em um anel comutativo, um ideal maximal com respeito a não ser principal é primo.^[9]
• Em um anel comutativo, um ideal maximal com respeito a não ser contavelmente gerado é primo.^[10]

Referências

• Goodearl, K. R.; Warfield, R. B., Jr. (2004), An introduction to noncommutative Noetherian rings, ISBN 0-521-54537-4, London Mathematical Society Student Texts, 61 2 ed. , Cambridge: Cambridge University Press, pp. xxiv+344, MR 2080008  !CS1 manut: Nomes múltiplos: lista de autores (link)
• Jacobson, Nathan (1989), Basic algebra. II, ISBN 0-7167-1933-9 2 ed. , New York: W. H. Freeman and Company, pp. xviii+686, MR 1009787 
• Kaplansky, Irving (1970), Commutative rings, Boston, Mass.: Allyn and Bacon Inc., pp. x+180, MR 0254021 
• Lam, T. Y. (2001), A first course in noncommutative rings, ISBN 0-387-95183-0, Graduate Texts in Mathematics, 131 2nd ed. , New York: Springer-Verlag, pp. xx+385, MR 1838439, Zbl 0980.16001 
• Lam, T. Y.; Reyes, Manuel L. (2008), «A prime ideal principle in commutative algebra», J. Algebra, ISSN 0021-8693, 319 (7): 3006–3027, MR 2397420, Zbl 1168.13002, doi:10.1016/j.jalgebra.2007.07.016 
• Hazewinkel, Michiel, ed. (2001), «Prime ideal», Enciclopédia de Matemática, ISBN 978-1-55608-010-4 (em inglês), Springer