Paralelepípedo

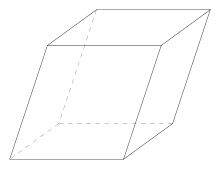
Paralelepípedo ou bloco retangular é a designação dada a um prisma cujas faces são paralelogramos.^[1][2] Um paralelepípedo tem seis faces, sendo que duas são idênticas e paralelas entre si.^[3] Os paralelepípedos podem ser retos ou oblíquos, consoante as suas faces laterais sejam perpendiculares ou não à base.^[4] O paralelepípedo possui 12 arestas 8 vértices e 6 faces.

Em geometria, um 'paralelepípedo' é uma forma tridimensional cujas 6 faces são paralelogramos. O paralelepípedo pode ser definido de três formas distintas:

• É um prisma cuja base é um paralelogramo;
• É um hexaedro do qual cada face é um paralelogramo;
• É um hexaedro com três pares de faces paralelas.

Os paralelepípedos constituem uma subclasse dos prismatoides.

Cada um dos três pares de faces paralelas do paralelepípedo pode ser considerado como a base, já que o prisma tem três conjuntos de quatro arestas paralelas, as quais, em cada conjunto, têm o mesmo comprimento.

O paralelepípedo pode ser encarado como o resultado da transformação linear de um cubo.

O volume de um paralelepípedo é o produto da área da sua base pela altura. Para este efeito a base pode ser qualquer das faces, sendo a altura medida perpendicularmente ao plano que contém a base. Por outro lado, se os vetores a = (a₁, a₂, a₃), b = (b₁, b₂, b₃) e c = (c₁, c₂, c₃) representarem as três arestas que se encontrem num vértice, então o volume do paralelepípedo é igual ao valor absoluto do produto triplo escalar a · (b × c), ou, o que é equivalente, ao valor absoluto do determinante:

${\displaystyle \left|\det {\begin{bmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{bmatrix}}\right|.}$

Para paralelepípedos com um plano de simetria existem dois casos:

• Têm quatro faces retangulares;
• Têm duas faces rômbicas, e das restantes, cada duas faces adjacentes são iguais (os dois pares são imagens invertidas entre si). Veja monoclínico.

• Um cuboide é um paralelepípedo onde todas as faces são retangulares.
• Um romboedro é um paralelepípedo com faces rômbicas congruentes entre si.
• Um cubo é um paralelepípedo com ambas as propriedades anteriores, isto é cujas faces são quadrados.

A designação paralelepípedo é também usada para formas análogas em espaços geométricos com mais de três dimensões.

A designação paralelepípedo, sem qualquer qualificativo, refere-se em geral à forma num espaço tridimensional, o percebido por nós. Num espaço n-dimensional, é comum usar-se a designação paralelepípedo n-dimensional, ou simplesmente n-paralelepípedo. Em 1D o análogo ao paralelepípedo é um intervalo, em 2D é um paralelogramo.

As diagonais de um n-paralelepípedo intersectam-se num ponto e são bissectadas pelo mesmo ponto. Uma Inversão neste ponto mantém o n-paralelepípedo inalterado. Veja o conceito de pontos fixos em grupos isométricos nos espaços euclidianos.

Referências

• Portal da geometria
• Portal da matemática