An bisect

Anul bisect ( din fr. bissexte, lat. bissextus) este un an calendaristic care are o zi în plus față de anii obișnuiți (sau, în cazul calendarelor lunisolare, o lună în plus) adăugată pentru a păstra anul calendaristic sincronizat cu anul astronomic sau cu cel sezonier.^[1] Întrucât anotimpurile și evenimentele astronomice nu se repetă într-un număr întreg de zile, calendarele care au același număr de zile în toți anii deviază încet în raport cu respectivele evenimente care ar trebui să aibă loc cu periodicitate de un an. Inserând (intercalând) o zi sau o lună suplimentară, această deviație se corectează.

De exemplu, în calendarul gregorian, fiecare an bisect are 366 de zile în loc de 365, prin prelungirea lunii februarie cu încă o zi, astfel ea având 29 de zile în loc de 28. La fel, în calendarul ebraic lunisolar, se adaugă luna Adar Aleph, a 13-a lună, de șapte ori într-o perioadă de 19 ani, la cele douăsprezece luni din anii obișnuiți pentru a evita deplasarea anului în raport cu anotimpurile.

În calendarul gregorian, o zi fixă din an avansează de la an la an cu o zi în săptămână, dar zilele de după 29 februarie dintr-un an bisect și cele de până la 28 februarie din anul următor vor avansa cu două zile din cauza zilei de 29 februarie. De exemplu, Crăciunul lui 2001 a fost într-o zi de marți, în 2002 miercuri, în 2003 joi, iar în 2004 a fost într-o sâmbătă.^[2]

În calendarul gregorian, calendar standard actualmente în aproape toată lumea, majoritatea anilor multipli de 4 sunt bisecți. În fiecare an bisect, luna februarie are 29 de zile în loc de 28. Adăugarea unei zile suplimentare la fiecare an compensează faptul că perioada de 365 de zile este mai scurtă decât un an tropic cu aproape 6 ore. Acest calendar a fost utilizat pentru prima oară în 1582.

Sunt necesare unele excepții de la această regulă simplă, întrucât durata anului tropical este puțin mai mică decât 365,25 zile. Eroarea se acumulează și pe o perioadă de 4 secole ea ajunge la 3 zile. Pentru aceasta, calendarul gregorian renunță la trei ani bisecți în 400 de ani. Aceasta se face prin renunțarea la ziua de 29 februarie în anii multipli de 100 și care nu sunt și multipli de 400.^[3] Anii 2000 și 2400 sunt ani bisecți, dar 1800, 1900, 2100, 2200, 2300 și 2500 nu sunt. Prin această regulă, numărul mediu de zile pe an este de 365 + ¹⁄₄ − ¹⁄₁₀₀ + ¹⁄₄₀₀ = 365,2425.^[4] Regula se poate aplica și la anii dinaintea reformei gregoriene (calendarul gregorian proleptic^{⁠(en)[traduceți]}), dacă se utilizează numerotarea astronomică a anilor^{⁠(en)[traduceți]}.^[5]

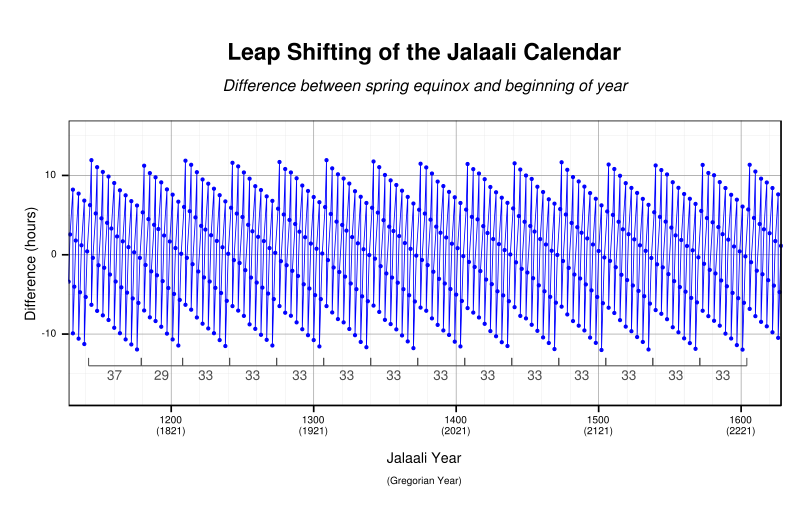
Acest grafic prezintă variațiile de dată și oră ale solstițiului din iunie cauzate de regula anilor bisecți neregulat temporizați. Comparați cu calendarul iranian solar Hijri, care are în general 8 zile adăugate la fiecare 33 de ani.

Calendarul gregorian a fost proiectat pentru a ține echinocțiul vernal în preajma datei de 21 martie, astfel că ziua de Paști (sărbătorită în duminica după prima lună plină {calculată după un calendar lunar} care cade în ziua de 21 martie sau după ea) să rămână aproape de acest echinocțiu.^[6]

Următorul pseudocod determină dacă un an este bisect sau nu în calendarul gregorian și calendarul gregorian proleptic înainte de 1582. Variabila year testată este numărul întreg reprezentând numărul anului în calendarul gregorian, și testele sunt aranjate pentru a trata cazul cel mai comun la început.

dacă (year nu este divizibil cu 4) atunci (an obișnuit)
altfel dacă (year nu este divizibil cu 100) atunci (an bisect)
altfel dacă (year nu este divizibil cu 400) atunci (an obișnuit)
altfel (an bisect)

sau

dacă (anul este divizibil cu 4 și anul nu este divizibil cu 100) atunci (an bisect)
dacă (anul este divizibil cu 400) atunci (an bisect)
altfel (an obișnuit)

Calendarul gregorian este o modificare a calendarului iulian utilizat pentru prima oară de romani. Calendarul roman a început ca un calendar lunisolar și își boteza zilele după fazele Lunii: luna nouă (calendae, de unde și „calendar”) și luna plină (Idus sau ide). Nonae erau denumite nu zilele care cădeau în primul pătrar, ci exact la o nundina (săptămână comercială romană) sau nouă zile înainte de ide, inclusiv numărând idele ca primele din aceste grupuri de nouă zile. Așa era denumită și o perioadă de opt zile. În 1825, Ideler^{⁠(en)[traduceți]} credea că acest calendar lunisolar fusese abandonat pe la 450 î.e.n. de către decemviri, care au implementat calendarul roman republican, utilizat până la 46 î.e.n. Zilele acestor calendare erau numărate înapoi (inclusiv) până la următoarea zi cu nume, astfel că 24 februarie era ante diem sextum Kalendas Martias („a șasea zi înainte de calendele lui martie”) adesea prescurtat a. d. VI Kal. Mart. Romanii numărau zilele cu includere, astfel că aceasta era de fapt a cincea zi dinainte de 1 martie în manieră modernă, cu excludere (neincluzând și ziua de început).^[7]

În calendarul republican, luna intercalată se insera în prima sau a doua zi după Terminalia^{⁠(en)[traduceți]} (a. d. VII Kal. Mar., 23 februarie). Restul zilelor lunii Februarius erau eliminate. Această lună modificată, denumită Intercalaris sau Mercedonius^{⁠(en)[traduceți]}, conținea 27 de zile. Festivalurile religioase ce se țineau de regulă în ultimele cinci zile ale lui februarie erau mutate în ultimele cinci zile ale lui Intercalaris. Întrucât se adăugau efectiv doar 22 sau 23 de zile, și nu un ciclu lunar complet, calendele și idele calendarului roman republican nu au mai fost asociate fazelor lunii.

Calendarul iulian, dezvoltat în anul 46 î.e.n. de Iulius Cezar, și intrat în vigoare în 45 î.e.n., a distribuit zece zile suplimentare printre zilele calendarului roman republican. Cezar a înlocuit și luna modificată printr-o singură zi suplimentară, plasată în locul lunii modificate. Pentru a trece la acest procedeu, ziua existentă și numită ante diem sextum Kalendas Martias (24 februarie) a fost dublată, producând ante diem bis sextum Kalendas Martias. Astfel, anul cu ziua dublată se numea bisect (bis sextum, „de două ori șase”). Din motive legale, cele două zile din bis sextum erau considerate o singură zi, a doua „jumătate” a acestei zile fiind suplimentară; în practica comună de până la 238, când scria Censorinus^{⁠(en)[traduceți]}, ziua suplimentară era urmată de ultimele cinci zile din februarie, a. d. VI, V, IV, III și pridie Kal. Mart. (zilele de 24, 25, 26, 27 și 28 de la începutul lui februarie într-un an obișnuit), astfel că ziua suplimentară era prima jumătate a zilei dublate. Astfel că ziua suplimentară a fost introdusă practic între a 23-a și a 24-a zi din februarie. Toți autorii de mai târziu, inclusiv Macrobius^{⁠(en)[traduceți]} pe la 430, Bede în 725, și alți calculatori medievali ai datei de Paști au continuat să afirme că bissextum (ziua bisectă) are loc înainte de ultimele cinci zile din februarie. Spre sfârșitul Evului Mediu timpuriu, s-a abandonat metoda romană de numerotare a zilelor, și de atunci ultima zi din luna februarie a anului bisect a început să fie considerată ziua adăugată la calendar.

Până la 1970, Biserica Romano-Catolică a sărbătorit întotdeauna ziua de Sfântul Matia la a. d. VI Kal. Mart., deci dacă zilele erau numărate de la începutul lunii, ea se numea 24 februarie în anii obișnuiți, dar prezența zilei suplimentare în anul bisect imediat înainte de a. d. VI Kal. Mart. a modificat ziua în 25 februarie în anii bisecți, veghea de Sfântul Matia trecea de la 23 februarie la 24 februarie. Această modificare nu a avut loc în Norvegia dinaintea Reformei și în Islanda; Papa Alexandru al III-lea a hotărât că oricare din cele două variante este legală (Liber Extra, 5. 40. 14. 1). Alte sărbători din perioada 25–28 februarie sunt și ele mutate în ziua următoare într-un an bisect (deși ar cădea în aceeași zi conform notației romane). Practica este încă urmată de cei ce folosesc vechile calendare.

Calendarul Bengalez^{⁠(en)[traduceți]} revizuit din Bangladesh și Calendarul Național Indian^{⁠(en)[traduceți]} își organizează anii modificați în așa fel încât ziua suplimentară să fie cât mai aproape de cea de 29 februarie în calendarul gregorian, pentru a simplifica conversia datelor cu acesta.

Calendarul solar tailandez^{⁠(en)[traduceți]} utilizează era budistă, dar este sincronizat cu cel gregorian din 1941 e.n.

Calendarul Bahá'í este structurat astfel încât ziua suplimentară cade întotdeauna în Ayyám-i-Há^{⁠(en)[traduceți]}, o perioadă de patru sau cinci zile începând cu ziua de 7 Esfand din calendarul solar Hejri, echivalentă aproximativ cu 26 februarie în calendarul gregorian.^[8]

În calendarul iulian, adăugarea unei zile la luna februarie a anilor multipli de 4 datează din anul 8 e.n.

Calendarul copt și cel etiopian adaugă și ele, o dată la patru ani, o zi la sfârșitul anului înainte de un 29 februarie al calendarului iulian.

Regula dă o medie de circa 365,25 zile pe an, cu 11 minute mai mult ca un an tropic. Aceasta înseamnă că echinocțiul vernal se deplasează cu o zi mai devreme în calendar o dată la 131 de ani.

Calendarul iulian revizuit^{⁠(en)[traduceți]} adaugă o zi suplimentară lunii februarie în anii care sunt multipli de patru, cu excepția anilor multipli de 100 care nu sunt echivalenți modulo 900 cu 200 sau cu 600. Această regulă îl face echivalent cu calendarul gregorian până în anul 2799. Primul an în care datele calendarului iulian revizuit nu vor mai fi conforme cu cele ale calendarului gregorian va fi 2800, deoarece acesta va fi an bisect în calendarul gregorian, dar nu și în cel iulian revizuit.

Regula dă o durată medie a anului de 365,242222 zile, o aproximație foarte bună a anului tropic mediu, dar, întrucât anul de la un echinocțiu vernal la altul este puțin mai mare, calendarul iulian revizuit nu are o performanță atât de bună ca cel gregorian la păstrarea echinocțiului vernal în ziua sau în preajma zilei de 21 martie.

Calendarul chinezesc este lunisolar, deci anul modificat are o întreagă lunăsuplimentară, denumită adesea lună embolismică după termenul grecesc. În calendarul chinezesc, luna suplimentară se adaugă după o regulă care asigură că luna a 11-a este întotdeauna cea care conține solstițiul de iarnă din emisfera nordică. Luna suplimentară ia același nume ca cea anterioară; de exemplu, dacă ea urmează după a doua lună (二月) atunci se numește pur și simplu „a doua lună adăugată”, de ex. chineză simplificată: 闰二月; chineză tradițională: 閏二月; pinyin: rùn'èryuè.

Calendarul ebraic este lunisolar cu lună embolismică. Această lună suplimentară se numește Adar Alef (primul Adar) și se adaugă după Adar, care atunci devine Adar Bet (al doilea Adar). Conform ciclului metonic^{⁠(en)[traduceți]}, aceasta se face de șapte ori în fiecare interval de nouăsprezece ani (anume, în anii 3, 6, 8, 11, 14, 17 și 19 ai intervalului). Aceasta este pentru a asigura că Pesah (Paștele evreiesc) este întotdeauna primăvara, după cum impune Torah (Pentateuch) în numeroase versete^[9] referitoare la Pesah.

În plus, calendarul evreiesc are reguli de amânare, prin care începutul anului poate fi amânat cu una sau două zile. Aceste reguli reduc numărul de combinații diferite ale lungimii anului cu ziua din săptămânăîn care începe el de la 28 la 14, și reglează poziția diferitelor sărbători religioase în raport cu Șabat. În particular, prima zi a anului ebraic nu poate fi niciodată duminică, miercuri sau vineri. Această regulă este denumită în ebraică „lo adu rosh” (לא אד"ו ראש), adică, "Rosh [ha-Shanah, prima zi a anului] nu este duminică, miercuri sau vineri” (întrucât cuvântul ebraic adu este scris cu trei litere ebraice ce semnifică duminică, miercuri și vineri). Ca atare, prima zi de Pesah (Paște) nu este niciodată luni, miercuri sau vineri. Această regulă este denumită în ebraică „lo badu Pesah” (לא בד"ו פסח), sintagmă cu înțeles dublu — „Pesah nu este o legendă”, dar și „Pesah nu este luni, miercuri sau vineri” (cuvântul ebraic badu fiind scris cu trei litere ce înseamnă luni, miercuri și vineri).

Un motiv pentru această regulă este că Yom Kippur, cea mai sfântă zi a calendarului ebraic și a zecea din anul ebraic, trebuie acum să nu fie niciodată adiacentă Șabatului săptămânal (care este sâmbăta), adică nu trebuie niciodată să cadă vineri sau duminică, pentru a nu avea două zile de Șabat consecutive. Yom Kippur poate totuși să fie într-o sâmbătă. Aceste reguli ale sărbătorilor nu se aplică anilor de la Facerea Lumii până la plecarea evreilor din Egipt conduși de Moise. La acel moment (cf. Exodul 13) Dumnezeul lui Abraham, Isaac și Iacob le-a dat evreilor „Legea”, inclusiv zilele pe care evreii trebuie să le țină sfinte și zilele de sărbătoare și de Șabat.

Anii care constau din 12 luni au între 353 și 355 de zile. Într-un an k'sidra („în ordine”) de 354 de zile, lunile au durate alternative de 30 și 29 de zile. Într-un an chaser („cu lipsă”) luna Kislev este redusă la 29 de zile. Într-un an malei („umplut”), luna Marcheshvan crește la 30 de zile. Anii de 13 luni urmează același șablon, cu adăugarea lunii de 30 de zile Adar Alef, care îi face să aibă între 383 și 385 de zile.

Versiunile calculată și observată ale calendarului islamic nu au zile adăugate în mod regulat, deși ambele au luni de 29 sau 30 de zile, în general în ordine alternantă. Calendarul islamic tabelar^{⁠(en)[traduceți]}, utilizat de astronomii musulmani în Evul Mediu și încă utilizat de unii musulmani, are însă o zi suplimentară adăugată la ultima lună a anului în 11 ani dintr-un ciclu de 30.^[10] Această zi suplimentară se găsește la sfârșitul ultimei luni, Dhu 'l-Hijja, care este și luna Hajjului.^[11]

Calendarul Hijri-Shamsi, adoptat și de comunitatea musulmană Ahmadiyya, se bazează pe calcule solare și este similar calendarului gregorian în structura sa cu excepția că primul an începe cu Hijra.^[12]

Calendarul iranian este un calendar observațional care începe cu echinocțiul de primăvară și adaugă o singură zi suplimentară la ultima lună (Esfand) o dată la fiecare patru sau cinci ani; primul astfel de an este al cincilea într-un ciclu tipic de 33 de ani și restul au loc o dată la patru ani în restul ciclului. Sistemul utilizat este mai exact, dar mai complicat, și se bazează pe ora la care este observat echinocțiului din martie de la Teheran. Perioada de 33 de ani nu este nici ea complet regulată; din când în când, ciclul de 33 de ani este întrerupt de un ciclu de 29 de ani. ^[13]