Тригонометрические функции

Рис. 1.
Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса

Тригонометри́ческие фу́нкции — элементарные функции^[1], которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла дуги в круге). Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число.

Раздел математики, изучающий свойства тригонометрических функций, называется тригонометрией.

К тригонометрическим функциям традиционно причисляют:

прямые тригонометрические функции:

синус ( $\sin x$ );
косинус ( $\cos x$ );

производные тригонометрические функции:

тангенс $\left(\mathrm {tg} \,x={\frac {\sin x}{\cos x}}\right)$ ;
котангенс $\left(\mathrm {ctg} \,x={\frac {\cos x}{\sin x}}\right)$ ;

секанс $\left(\sec x={\frac {1}{\cos x}}\right)$ ;
косеканс $\left(\mathrm {cosec} \,x={\frac {1}{\sin x}}\right)$ ;

обратные тригонометрические функции:

арксинус, арккосинус и т. д.

В типографике литературы на разных языках сокращённое обозначение тригонометрических функций различно, например, в англоязычной литературе тангенс, котангенс и косеканс обозначаются $\tan x$ , $\cot x$ , $\csc x$ . До Второй мировой войны в Германии и во Франции эти функции обозначались так же, как принято в русскоязычных текстах^[2], но потом в литературе на языках этих стран был принят англоязычный вариант записи тригонометрических функций.

Кроме этих шести широко известных тригонометрических функций, иногда в литературе используются некоторые редко используемые тригонометрические функции (версинус и т. д.).

Синус и косинус вещественного аргумента представляют собой периодические, непрерывные и бесконечно дифференцируемые вещественнозначные функции. Остальные четыре функции на вещественной оси также вещественнозначны, периодичны и бесконечно дифференцируемы, за исключением счётного числа разрывов второго рода: у тангенса и секанса в точках $\pm \pi n+{\frac {\pi }{2}}$ , а у котангенса и косеканса — в точках $\pm \pi n$ .
Графики тригонометрических функций показаны на рис. 1.

Способы определения[править | править код]

Определение для острых углов[править | править код]

Рис. 4.
Тригонометрические функции острого угла

В геометрии тригонометрические функции острого угла определяются отношениями сторон прямоугольного треугольника^[3]. Пусть $\triangle AOB$ — прямоугольный, с острым углом $\angle AOB=\alpha$ и гипотенузой $OB$ . Тогда:

$\sin \alpha ={\frac {AB}{OB}}$ (синусом угла $\alpha$ называется отношение противолежащего катета к гипотенузе);
$\cos \alpha ={\frac {OA}{OB}}$ (косинусом угла $\alpha$ называется отношение прилежащего катета к гипотенузе);
$\mathrm {tg} \,\alpha ={\frac {AB}{OA}}$ (тангенсом угла $\alpha$ называется отношение противолежащего катета к прилежащему);
$\mathrm {ctg} \,\alpha ={\frac {OA}{AB}}$ (котангенсом угла $\alpha$ называется отношение прилежащего катета к противолежащему);
$\mathrm {sec} \,\alpha ={\frac {OB}{OA}}$ (секансом угла $\alpha$ называется отношение гипотенузы к прилежащему катету);
$\mathrm {cosec} \,\alpha ={\frac {OB}{AB}}$ (косекансом угла $\alpha$ называется отношение гипотенузы к противолежащему катету).

Данное определение имеет некоторое методическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач о тупоугольных треугольниках. (См.: теорема синусов, теорема косинусов).

Определение для любых углов[править | править код]

Рис. 2.
Определение тригонометрических функций

Обычно тригонометрические функции определяются геометрически^[4]. В декартовой системе координат на плоскости построим окружность единичного радиуса ( $R=1$ ) с центром в начале координат $O$ . Всякий угол станем рассматривать как поворот от положительного направления оси абсцисс до некоторого луча $OB$ (точку $B$ выбираем на окружности), при этом направление поворота против часовой стрелки считаем положительным, а по часовой стрелке — отрицательным. Абсциссу точки $B$ обозначим $x_{B}$ , а ординату — $y_{B}$ (см. рисунок 2).

Рис. 3.
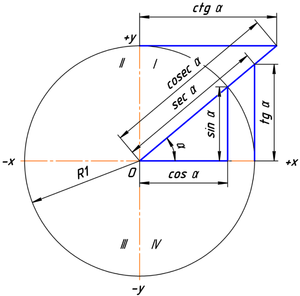
Численные значения тригонометрических функций угла

\alpha

в тригонометрической окружности с радиусом, равным единице

Определим функции следующим образом:

$\sin \alpha =y_{B}$ , $\cos \alpha =x_{B}$ ;
$\operatorname {tg} \alpha ={\frac {y_{B}}{x_{B}}}$ , $\operatorname {ctg} \alpha ={\frac {x_{B}}{y_{B}}}$ ;
$\sec \alpha ={\frac {1}{x_{B}}}$ , $\operatorname {cosec} \alpha ={\frac {1}{y_{B}}}$ .

Нетрудно видеть, что такое определение так же основывается на отношениях прямоугольного треугольника, с тем отличием, что учитывается знак ( $\pm 1$ ). Поэтому тригонометрические функции можно определить и по окружности произвольного радиуса $R$ , однако формулы придётся нормировать. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.

В тригонометрии удобным оказывается вести счёт углов не в градусной мере, а в радианной. Так, угол в $360^{\circ }$ запишется длиной единичной окружности $2\pi$ . Угол в $180^{\circ }$ равен, соответственно $\pi$ и так далее. Заметим, что угол на $2\pi$ отличающийся от $\alpha$ по рисунку эквивалентен $\alpha$ , вследствие чего заключим, что тригонометрические функции периодичны.

Наконец, определим тригонометрические функции вещественного числа $x$ тригонометрическими функциями угла, радианная мера которого равна $x$ .

Определение как решений дифференциальных уравнений[править | править код]

Синус и косинус можно определить как единственные функции, вторые производные которых равны самим функциям, взятым со знаком минус:

\ \left(\cos x\right)''=-\cos x,

\ \left(\sin x\right)''=-\sin x.

То есть задать их как чётное (косинус) и нечётное (синус) решения дифференциального уравнения

{\frac {d^{2}}{d\varphi ^{2}}}R(\varphi )=-R(\varphi ),

с дополнительными условиями: $R(0)=1$ для косинуса и $R'(0)=1$ для синуса.

Определение как решений функциональных уравнений[править | править код]

Функции косинус и синус можно определить^[5] как решения ( $f$ и $g$ соответственно) системы функциональных уравнений:

$\left\{{\begin{array}{rcl}f(x+y)&=&f(x)f(y)-g(x)g(y)\\g(x+y)&=&g(x)f(y)+f(x)g(y)\end{array}}\right.$

при дополнительных условиях:

$f(x)^{2}+g(x)^{2}=1,$ $g(\pi /2)=1,$ и $0<g(x)<1$ при $0<x<\pi /2$ .

Определение через ряды[править | править код]

Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу, и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:

\sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+{\frac {x^{9}}{9!}}-\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}},

\cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+{\frac {x^{8}}{8!}}-\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.

Пользуясь этими формулами, а также равенствами $\operatorname {tg} \,x={\frac {\sin x}{\cos x}},$ $\operatorname {ctg} \,x={\frac {\cos x}{\sin x}},$ $\sec x={\frac {1}{\cos x}}$ и $\operatorname {cosec} \,x={\frac {1}{\sin x}},$ можно найти разложения в ряд и других тригонометрических функций:

{\operatorname {tg} \,x=x+{\frac {1}{3}}\,x^{3}+{\frac {2}{15}}\,x^{5}+{\frac {17}{315}}\,x^{7}+{\frac {62}{2835}}\,x^{9}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)|B_{2n}|}{(2n)!}}x^{2n-1}\quad \left(-{\frac {\pi }{2}}<x<{\frac {\pi }{2}}\right),}

{\operatorname {ctg} \,x={\frac {1}{x}}-{\frac {x}{3}}-{\frac {x^{3}}{45}}-{\frac {2x^{5}}{945}}-{\frac {x^{7}}{4725}}-\cdots ={\frac {1}{x}}-\sum _{n=1}^{\infty }{\frac {2^{2n}|B_{2n}|}{(2n)!}}\,x^{2n-1}\quad \left(-\pi <x<\pi \right),}

{\sec x=1+{\frac {1}{2}}\,x^{2}+{\frac {5}{24}}\,x^{4}+{\frac {61}{720}}\,x^{6}+{\frac {277}{8064}}\,x^{8}+\cdots =\sum _{n=0}^{\infty }{\frac {|E_{n}|}{(2n)!}}\,x^{2n},\quad \left(-{\frac {\pi }{2}}<x<{\frac {\pi }{2}}\right),}

\operatorname {cosec} x={\frac {1}{x}}+{\frac {1}{6}}\,x+{\frac {7}{360}}\,x^{3}+{\frac {31}{15120}}\,x^{5}+{\frac {127}{604800}}\,x^{7}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2(2^{2n-1}-1)|B_{2n}|}{(2n)!}}\,x^{2n-1}\quad \left(-\pi <x<\pi \right),

где

B_{n}

— числа Бернулли,

E_{n}

— числа Эйлера.

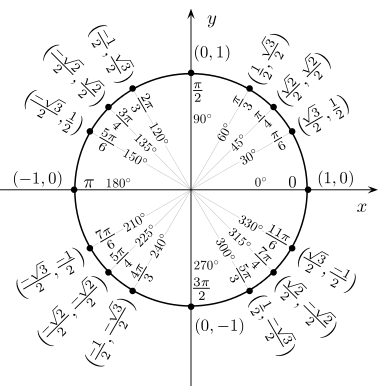
Значения тригонометрических функций для некоторых углов[править | править код]

Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. (« $\infty$ » означает, что функция в указанной точке не определена, а в её окрестности стремится к бесконечности).

Значения косинуса и синуса на окружности

Радианы	$0$	${\frac {\pi }{6}}$	${\frac {\pi }{4}}$	${\frac {\pi }{3}}$	${\frac {\pi }{2}}$	$\pi$	${\frac {3\pi }{2}}$	$2\pi$
Градусы	$0^{\circ }$	$30^{\circ }$	$45^{\circ }$	$60^{\circ }$	$90^{\circ }$	$180^{\circ }$	$270^{\circ }$	$360^{\circ }$
$\sin \alpha$	$0$	${\frac {1}{2}}$	${\frac {\sqrt {2}}{2}}$	${\frac {\sqrt {3}}{2}}$	$1$	$0$	$-1$	$0$
$\cos \alpha$	$1$	${\frac {\sqrt {3}}{2}}$	${\frac {\sqrt {2}}{2}}$	${\frac {1}{2}}$	$0$	$-1$	$0$	$1$
$\operatorname {tg} \,\alpha$	$0$	${\frac {1}{\sqrt {3}}}$	$1$	${\sqrt {3}}$	$\infty$	$0$	$\infty$	$0$
$\operatorname {ctg} \,\alpha$	$\infty$	${\sqrt {3}}$	$1$	${\frac {\sqrt {3}}{3}}$	$0$	$\infty$	$0$	$\infty$
$\sec \alpha$	$1$	${\frac {2{\sqrt {3}}}{3}}$	${\sqrt {2}}$	$2$	$\infty$	$-1$	$\infty$	$1$
$\operatorname {cosec} \,\alpha$	$\infty$	$2$	${\sqrt {2}}$	${\frac {2{\sqrt {3}}}{3}}$	$1$	$\infty$	$-1$	$\infty$

Значения тригонометрических функций нестандартных углов[править | править код]

Радианы	${\frac {2\pi }{3}}$	${\frac {3\pi }{4}}$	${\frac {5\pi }{6}}$	${\frac {7\pi }{6}}$	${\frac {5\pi }{4}}$	${\frac {4\pi }{3}}$	${\frac {5\pi }{3}}$	${\frac {7\pi }{4}}$	${\frac {11\pi }{6}}$
Градусы	$120^{\circ }$	$135^{\circ }$	$150^{\circ }$	$210^{\circ }$	$225^{\circ }$	$240^{\circ }$	$300^{\circ }$	$315^{\circ }$	$330^{\circ }$
$\sin \alpha$	${\frac {\sqrt {3}}{2}}$	${\frac {\sqrt {2}}{2}}$	${\frac {1}{2}}$	$-{\frac {1}{2}}$	$-{\frac {\sqrt {2}}{2}}$	$-{\frac {\sqrt {3}}{2}}$	$-{\frac {\sqrt {3}}{2}}$	$-{\frac {\sqrt {2}}{2}}$	$-{\frac {1}{2}}$
$\cos \alpha$	$-{\frac {1}{2}}$	$-{\frac {\sqrt {2}}{2}}$	$-{\frac {\sqrt {3}}{2}}$	$-{\frac {\sqrt {3}}{2}}$	$-{\frac {\sqrt {2}}{2}}$	$-{\frac {1}{2}}$	${\frac {1}{2}}$	${\frac {\sqrt {2}}{2}}$	${\frac {\sqrt {3}}{2}}$
$\operatorname {tg} \,\alpha$	$-{\sqrt {3}}$	$-1$	$-{\frac {\sqrt {3}}{3}}$	${\frac {\sqrt {3}}{3}}$	$1$	${\sqrt {3}}$	$-{\sqrt {3}}$	$-1$	$-{\frac {\sqrt {3}}{3}}$
$\operatorname {ctg} \,\alpha$	$-{\frac {\sqrt {3}}{3}}$	$-1$	$-{\sqrt {3}}$	${\sqrt {3}}$	$1$	${\frac {\sqrt {3}}{3}}$	$-{\frac {\sqrt {3}}{3}}$	$-1$	$-{\sqrt {3}}$
$\sec \alpha$	$-2$	$-{\sqrt {2}}$	$-{\frac {2{\sqrt {3}}}{3}}$	$-{\frac {2{\sqrt {3}}}{3}}$	$-{\sqrt {2}}$	$-2$	$2$	${\sqrt {2}}$	${\frac {2{\sqrt {3}}}{3}}$
$\operatorname {cosec} \,\alpha$	${\frac {2{\sqrt {3}}}{3}}$	${\sqrt {2}}$	$2$	$-2$	$-{\sqrt {2}}$	$-{\frac {2{\sqrt {3}}}{3}}$	$-{\frac {2{\sqrt {3}}}{3}}$	$-{\sqrt {2}}$	$-2$

Радианы	${\frac {\pi }{12}}$	${\frac {\pi }{10}}$	${\frac {\pi }{8}}$	${\frac {\pi }{5}}$	${\frac {3\pi }{10}}$	${\frac {3\pi }{8}}$	${\frac {2\pi }{5}}$	${\frac {5\pi }{12}}$
Градусы	$15^{\circ }$	$18^{\circ }$	$22{,}5^{\circ }$	$36^{\circ }$	$54^{\circ }$	$67{,}5^{\circ }$	$72^{\circ }$	$75^{\circ }$
$\sin \alpha$	${\frac {\sqrt {2-{\sqrt {3}}}}{2}}$	${\frac {{\sqrt {5}}-1}{4}}$	${\frac {\sqrt {2-{\sqrt {2}}}}{2}}$	${\frac {\sqrt {10-2{\sqrt {5}}}}{4}}$	${\frac {{\sqrt {5}}+1}{4}}$	${\frac {\sqrt {2+{\sqrt {2}}}}{2}}$	${\frac {\sqrt {10+2{\sqrt {5}}}}{4}}$	${\frac {\sqrt {2+{\sqrt {3}}}}{2}}$
$\cos \alpha$	${\frac {\sqrt {2+{\sqrt {3}}}}{2}}$	${\frac {\sqrt {10+2{\sqrt {5}}}}{4}}$	${\frac {\sqrt {2+{\sqrt {2}}}}{2}}$	${\frac {{\sqrt {5}}+1}{4}}$	${\frac {\sqrt {10-2{\sqrt {5}}}}{4}}$	${\frac {\sqrt {2-{\sqrt {2}}}}{2}}$	${\frac {{\sqrt {5}}-1}{4}}$	${\frac {\sqrt {2-{\sqrt {3}}}}{2}}$
$\operatorname {tg} \,\alpha$	$2-{\sqrt {3}}$	${\frac {\sqrt {25-10{\sqrt {5}}}}{5}}$	${\sqrt {2}}-1$	${\sqrt {5-2{\sqrt {5}}}}$	${\frac {\sqrt {25+10{\sqrt {5}}}}{5}}$	${\sqrt {2}}+1$	${\sqrt {5+2{\sqrt {5}}}}$	$2+{\sqrt {3}}$
$\operatorname {ctg} \,\alpha$	$2+{\sqrt {3}}$	${\sqrt {5+2{\sqrt {5}}}}$	${\sqrt {2}}+1$	${\frac {\sqrt {25+10{\sqrt {5}}}}{5}}$	${\sqrt {5-2{\sqrt {5}}}}$	${\sqrt {2}}-1$	${\frac {\sqrt {25-10{\sqrt {5}}}}{5}}$	$2-{\sqrt {3}}$
$\sec \alpha$	$2{\sqrt {2-{\sqrt {3}}}}$	${\frac {\sqrt {50-10{\sqrt {5}}}}{5}}$	${\sqrt {4-2{\sqrt {2}}}}$	${\sqrt {5}}-1$	${\frac {\sqrt {50+10{\sqrt {5}}}}{5}}$	${\sqrt {4+2{\sqrt {2}}}}$	${\sqrt {5}}+1$	$2{\sqrt {2+{\sqrt {3}}}}$
$\operatorname {cosec} \,\alpha$	$2{\sqrt {2+{\sqrt {3}}}}$	${\sqrt {5}}+1$	${\sqrt {4+2{\sqrt {2}}}}$	${\frac {\sqrt {50+10{\sqrt {5}}}}{5}}$	${\sqrt {5}}-1$	${\sqrt {4-2{\sqrt {2}}}}$	${\frac {\sqrt {50-10{\sqrt {5}}}}{5}}$	$2{\sqrt {2-{\sqrt {3}}}}$

Значения тригонометрических функций для некоторых других углов

$\sin {\frac {\pi }{60}}=\cos {\frac {29\,\pi }{60}}=\sin 3^{\circ }=\cos 87^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}+1)({\sqrt {5}}-1)-2({\sqrt {3}}-1){\sqrt {5+{\sqrt {5}}}}}{16}},$

$\cos {\frac {\pi }{60}}=\sin {\frac {29\,\pi }{60}}=\cos 3^{\circ }=\sin 87^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}-1)({\sqrt {5}}-1)+2({\sqrt {3}}+1){\sqrt {5+{\sqrt {5}}}}}{16}},$

$\operatorname {tg} {\frac {\pi }{60}}=\operatorname {ctg} {\frac {29\,\pi }{60}}=\operatorname {tg} 3^{\circ }=\operatorname {ctg} 87^{\circ }={\frac {2({\sqrt {5}}+2)-{\sqrt {3}}({\sqrt {5}}+3)+(2-{\sqrt {3}})({\sqrt {3}}({\sqrt {5}}+1)-2){\sqrt {5-2{\sqrt {5}}}}}{2}},$

$\operatorname {ctg} {\frac {\pi }{60}}=\operatorname {tg} {\frac {29\,\pi }{60}}=\operatorname {ctg} 3^{\circ }=\operatorname {tg} 87^{\circ }={\frac {2(2({\sqrt {5}}+2)+{\sqrt {3}}({\sqrt {5}}+3))+({\sqrt {3}}({\sqrt {5}}-1)+2){\sqrt {2(25+11{\sqrt {5}})}}}{4}},$

$\sin {\frac {\pi }{30}}=\cos {\frac {7\,\pi }{15}}=\sin 6^{\circ }=\cos 84^{\circ }={\frac {{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1}{8}},$

$\cos {\frac {\pi }{30}}=\sin {\frac {7\,\pi }{15}}=\cos 6^{\circ }=\sin 84^{\circ }={\frac {{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)}{8}},$

$\operatorname {tg} {\frac {\pi }{30}}=\operatorname {ctg} {\frac {7\,\pi }{15}}=\operatorname {tg} 6^{\circ }=\operatorname {ctg} 84^{\circ }={\frac {{\sqrt {2(5-{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)}{2}},$

$\operatorname {ctg} {\frac {\pi }{30}}=\operatorname {tg} {\frac {7\,\pi }{15}}=\operatorname {ctg} 6^{\circ }=\operatorname {tg} 84^{\circ }={\frac {{\sqrt {2(25+11{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+3)}{2}},$

$\sin {\frac {\pi }{20}}=\cos {\frac {9\,\pi }{20}}=\sin 9^{\circ }=\cos 81^{\circ }={\frac {{\sqrt {2}}({\sqrt {5}}+1)-2{\sqrt {5-{\sqrt {5}}}}}{8}},$

$\cos {\frac {\pi }{20}}=\sin {\frac {9\,\pi }{20}}=\cos 9^{\circ }=\sin 81^{\circ }={\frac {{\sqrt {2}}({\sqrt {5}}+1)+2{\sqrt {5-{\sqrt {5}}}}}{8}},$

$\operatorname {tg} {\frac {\pi }{20}}=\operatorname {ctg} {\frac {9\,\pi }{20}}=\operatorname {tg} 9^{\circ }=\operatorname {ctg} 81^{\circ }={{\sqrt {5}}+1-{\sqrt {5+2{\sqrt {5}}}}},$

$\operatorname {ctg} {\frac {\pi }{20}}=\operatorname {tg} {\frac {9\,\pi }{20}}=\operatorname {ctg} 9^{\circ }=\operatorname {tg} 81^{\circ }={{\sqrt {5}}+1+{\sqrt {5+2{\sqrt {5}}}}},$

$\sin {\frac {\pi }{15}}=\cos {\frac {13\,\pi }{30}}=\sin 12^{\circ }=\cos 78^{\circ }={\frac {{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)}{8}},$

$\cos {\frac {\pi }{15}}=\sin {\frac {13\,\pi }{30}}=\cos 12^{\circ }=\sin 78^{\circ }={\frac {{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1}{8}},$

$\operatorname {tg} {\frac {\pi }{15}}=\operatorname {ctg} {\frac {13\,\pi }{30}}=\operatorname {tg} 12^{\circ }=\operatorname {ctg} 78^{\circ }={\frac {{\sqrt {3}}(3-{\sqrt {5}})-{\sqrt {2(25-11{\sqrt {5}})}}}{2}},$

$\operatorname {ctg} {\frac {\pi }{15}}=\operatorname {tg} {\frac {13\,\pi }{30}}=\operatorname {ctg} 12^{\circ }=\operatorname {tg} 78^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}+1)+{\sqrt {2(5+{\sqrt {5}})}}}{2}},$

$\sin {\frac {7\,\pi }{60}}=\cos {\frac {23\,\pi }{60}}=\sin 21^{\circ }=\cos 69^{\circ }={\frac {-{\sqrt {2}}({\sqrt {3}}-1)({\sqrt {5}}+1)+2({\sqrt {3}}+1){\sqrt {5-{\sqrt {5}}}}}{16}},$

$\cos {\frac {7\,\pi }{60}}=\sin {\frac {23\,\pi }{60}}=\cos 21^{\circ }=\sin 69^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}+1)({\sqrt {5}}+1)+2({\sqrt {3}}-1){\sqrt {5-{\sqrt {5}}}}}{16}},$

$\operatorname {tg} {\frac {7\,\pi }{60}}=\operatorname {ctg} {\frac {23\,\pi }{60}}=\operatorname {tg} 21^{\circ }=\operatorname {ctg} 69^{\circ }={\frac {2(2({\sqrt {5}}-2)-{\sqrt {3}}(3-{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}+1)-2){\sqrt {2(25-11{\sqrt {5}})}}}{4}},$

$\operatorname {ctg} {\frac {7\,\pi }{60}}=\operatorname {tg} {\frac {23\,\pi }{60}}=\operatorname {ctg} 21^{\circ }=\operatorname {tg} 69^{\circ }={\frac {2(2({\sqrt {5}}-2)+{\sqrt {3}}(3-{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}+1)+2){\sqrt {2(25-11{\sqrt {5}})}}}{4}},$

$\sin {\frac {2\,\pi }{15}}=\cos {\frac {11\,\pi }{30}}=\sin 24^{\circ }=\cos 66^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}+1)-{\sqrt {2(5-{\sqrt {5}})}}}{8}},$

$\cos {\frac {2\,\pi }{15}}=\sin {\frac {11\,\pi }{30}}=\cos 24^{\circ }=\sin 66^{\circ }={\frac {{\sqrt {5}}+1+{\sqrt {6(5-{\sqrt {5}})}}}{8}},$

$\operatorname {tg} {\frac {2\,\pi }{15}}=\operatorname {ctg} {\frac {11\,\pi }{30}}=\operatorname {tg} 24^{\circ }=\operatorname {ctg} 66^{\circ }={\frac {-{\sqrt {3}}(3+{\sqrt {5}})+{\sqrt {2(25+11{\sqrt {5}})}}}{2}},$

$\operatorname {ctg} {\frac {2\,\pi }{15}}=\operatorname {tg} {\frac {11\,\pi }{30}}=\operatorname {ctg} 24^{\circ }=\operatorname {tg} 66^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}-1)+{\sqrt {2(5-{\sqrt {5}})}}}{2}},$

$\sin {\frac {3\,\pi }{20}}=\cos {\frac {7\,\pi }{20}}=\sin 27^{\circ }=\cos 63^{\circ }={\frac {-{\sqrt {2}}({\sqrt {5}}-1)+2{\sqrt {5+{\sqrt {5}}}}}{8}},$

$\cos {\frac {3\,\pi }{20}}=\sin {\frac {7\,\pi }{20}}=\cos 27^{\circ }=\sin 63^{\circ }={\frac {{\sqrt {2}}({\sqrt {5}}-1)+2{\sqrt {5+{\sqrt {5}}}}}{8}},$

$\operatorname {tg} {\frac {3\,\pi }{20}}=\operatorname {ctg} {\frac {7\,\pi }{20}}=\operatorname {tg} 27^{\circ }=\operatorname {ctg} 63^{\circ }={{\sqrt {5}}-1-{\sqrt {5-2{\sqrt {5}}}}},$

$\operatorname {ctg} {\frac {3\,\pi }{20}}=\operatorname {tg} {\frac {7\,\pi }{20}}=\operatorname {ctg} 27^{\circ }=\operatorname {tg} 63^{\circ }={{\sqrt {5}}-1+{\sqrt {5-2{\sqrt {5}}}}},$

$\sin {\frac {11\,\pi }{60}}=\cos {\frac {19\,\pi }{60}}=\sin 33^{\circ }=\cos 57^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}+1)({\sqrt {5}}-1)+2({\sqrt {3}}-1){\sqrt {5+{\sqrt {5}}}}}{16}},$

$\cos {\frac {11\,\pi }{60}}=\sin {\frac {19\,\pi }{60}}=\cos 33^{\circ }=\sin 57^{\circ }={\frac {-{\sqrt {2}}({\sqrt {3}}-1)({\sqrt {5}}-1)+2({\sqrt {3}}+1){\sqrt {5+{\sqrt {5}}}}}{16}},$

$\operatorname {tg} {\frac {11\,\pi }{60}}=\operatorname {ctg} {\frac {19\,\pi }{60}}=\operatorname {tg} 33^{\circ }=\operatorname {ctg} 57^{\circ }={\frac {-2({\sqrt {5}}+2)+{\sqrt {3}}(3+{\sqrt {5}})+(2-{\sqrt {3}})({\sqrt {3}}({\sqrt {5}}+1)-2){\sqrt {5-2{\sqrt {5}}}}}{2}},$

$\operatorname {ctg} {\frac {11\,\pi }{60}}=\operatorname {tg} {\frac {19\,\pi }{60}}=\operatorname {ctg} 33^{\circ }=\operatorname {tg} 57^{\circ }={\frac {-2(2({\sqrt {5}}+2)+{\sqrt {3}}(3+{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}-1)+2){\sqrt {2(25+11{\sqrt {5}})}}}{4}},$

$\sin {\frac {13\,\pi }{60}}=\cos {\frac {17\,\pi }{60}}=\sin 39^{\circ }=\cos 51^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}+1)({\sqrt {5}}+1)-2({\sqrt {3}}-1){\sqrt {5-{\sqrt {5}}}}}{16}},$

$\cos {\frac {13\,\pi }{60}}=\sin {\frac {17\,\pi }{60}}=\cos 39^{\circ }=\sin 51^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}-1)({\sqrt {5}}+1)+2({\sqrt {3}}+1){\sqrt {5-{\sqrt {5}}}}}{16}},$

$\operatorname {tg} {\frac {13\,\pi }{60}}=\operatorname {ctg} {\frac {17\,\pi }{60}}=\operatorname {tg} 39^{\circ }=\operatorname {ctg} 51^{\circ }={\frac {-2(2({\sqrt {5}}-2)+{\sqrt {3}}(3-{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}+1)+2){\sqrt {2(25-11{\sqrt {5}})}}}{4}},$

$\operatorname {ctg} {\frac {13\,\pi }{60}}=\operatorname {tg} {\frac {17\,\pi }{60}}=\operatorname {ctg} 39^{\circ }=\operatorname {tg} 51^{\circ }={\frac {-2(2({\sqrt {5}}-2)-{\sqrt {3}}(3-{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}+1)-2){\sqrt {2(25-11{\sqrt {5}})}}}{4}},$

$\sin {\frac {7\,\pi }{30}}=\cos {\frac {8\,\pi }{30}}=\sin 42^{\circ }=\cos 48^{\circ }={\frac {-({\sqrt {5}}-1)+{\sqrt {6(5+{\sqrt {5}})}}}{8}},$

$\cos {\frac {7\,\pi }{30}}=\sin {\frac {8\,\pi }{30}}=\cos 42^{\circ }=\sin 48^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}-1)+{\sqrt {2(5+{\sqrt {5}})}}}{8}},$

$\operatorname {tg} {\frac {7\,\pi }{30}}=\operatorname {ctg} {\frac {8\,\pi }{30}}=\operatorname {tg} 42^{\circ }=\operatorname {ctg} 48^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}+1)-{\sqrt {2(5+{\sqrt {5}})}}}{2}},$

$\operatorname {ctg} {\frac {7\,\pi }{30}}=\operatorname {tg} {\frac {8\,\pi }{30}}=\operatorname {ctg} 42^{\circ }=\operatorname {tg} 48^{\circ }={\frac {{\sqrt {3}}(3-{\sqrt {5}})+{\sqrt {2(25-11{\sqrt {5}})}}}{2}},$

$\operatorname {tg} {\frac {\pi }{120}}=\operatorname {ctg} {\frac {59\,\pi }{120}}=\operatorname {tg} 1.5^{\circ }=\operatorname {ctg} 88.5^{\circ }={\sqrt {\frac {8-{\sqrt {2(2-{\sqrt {3}})(3-{\sqrt {5}})}}-{\sqrt {2(2+{\sqrt {3}})(5+{\sqrt {5}})}}}{8+{\sqrt {2(2-{\sqrt {3}})(3-{\sqrt {5}})}}+{\sqrt {2(2+{\sqrt {3}})(5+{\sqrt {5}})}}}}},$

$\cos {\frac {\pi }{240}}=\sin {\frac {119\,\pi }{240}}=\cos 0.75^{\circ }=\sin 89.25^{\circ }={\frac {1}{16}}\left({\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}\left({\sqrt {2(5+{\sqrt {5}})}}+{\sqrt {3}}(1-{\sqrt {5}})\right)+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}\left({\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1\right)\right),$

$\cos {\frac {\pi }{17}}=\sin {\frac {15\,\pi }{34}}={\frac {1}{8}}{\sqrt {2\left(2{\sqrt {3{\sqrt {17}}-{\sqrt {2(85+19{\sqrt {17}})}}+17}}+{\sqrt {2(17-{\sqrt {17}})}}+{\sqrt {17}}+15\right)}}.$

$\sin {\pi \over 2^{n+1}}={1 \over 2}\underbrace {\sqrt {2-{\sqrt {2+\dots +{\sqrt {2}}}}}} _{n},n\in \mathbb {N}$

$\cos {\pi \over 2^{n+1}}={1 \over 2}\underbrace {\sqrt {2+{\sqrt {2+\dots +{\sqrt {2}}}}}} _{n},n\in \mathbb {N}$

$\sin {\pi \over 3\cdot 2^{n}}={1 \over 2}\underbrace {\sqrt {2-{\sqrt {2+\dots +{\sqrt {3}}}}}} _{n},n\geq 2$

$\cos {\pi \over 3\cdot 2^{n}}={1 \over 2}\underbrace {\sqrt {2+{\sqrt {2+\dots +{\sqrt {3}}}}}} _{n},n\geq 2$

Свойства тригонометрических функций[править | править код]

Простейшие тождества[править | править код]

Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности ( $x^{2}+y^{2}=1$ ) или теореме Пифагора, имеем:

\sin ^{2}\alpha +\cos ^{2}\alpha =1.

Это соотношение называется основным тригонометрическим тождеством.

Разделив это уравнение на квадрат косинуса и синуса соответственно, получим:

1+\mathop {\mathrm {tg} } \,^{2}\alpha =\mathop {\mathrm {sec} } \,^{2}\alpha ,

1+\mathop {\mathrm {ctg} } \,^{2}\alpha =\mathop {\mathrm {cosec} } \,^{2}\alpha .

Из определения тангенса и котангенса следует, что

\mathop {\mathrm {tg} } \,\alpha \cdot \mathop {\mathrm {ctg} } \,\alpha =1.

Любую тригонометрическую функцию можно выразить через любую другую тригонометрическую функцию с тем же аргументом (с точностью до знака из-за неоднозначности раскрытия квадратного корня). Нижеприведённые формулы верны для $0<x<\pi /2$ :

	sin	cos	tg	ctg	sec	cosec
$\,\sin x=$	$\,\sin x$	${\sqrt {1-\cos ^{2}x}}$	${\frac {\operatorname {tg} x}{\sqrt {1+\operatorname {tg} ^{2}x}}}$	${\frac {1}{\sqrt {\operatorname {ctg} ^{2}x+1}}}$	${\frac {\sqrt {\sec ^{2}x-1}}{\sec x}}$	${\frac {1}{\operatorname {cosec} x}}$
$\,\cos x=$	$\,{\sqrt {1-\sin ^{2}x}}$	$\,\cos x$	$\,{\frac {1}{\sqrt {1+\operatorname {tg} ^{2}x}}}$	$\,{\frac {\operatorname {ctg} x}{\sqrt {\operatorname {ctg} ^{2}x+1}}}$	$\,{\frac {1}{\sec x}}$	$\,{\frac {\sqrt {\operatorname {cosec} ^{2}x-1}}{\operatorname {cosec} x}}$
$\,\operatorname {tg} x=$	$\,{\frac {\sin x}{\sqrt {1-\sin ^{2}x}}}$	$\,{\frac {\sqrt {1-\cos ^{2}x}}{\cos x}}$	$\,\operatorname {tg} x$	$\,{\frac {1}{\operatorname {ctg} x}}$	$\,{\sqrt {\sec ^{2}x-1}}$	$\,{\frac {1}{\sqrt {\operatorname {cosec} ^{2}x-1}}}$
$\,\operatorname {ctg} x=$	$\,{\frac {\sqrt {1-\sin ^{2}x}}{\sin x}}$	$\,{\frac {\cos x}{\sqrt {1-\cos ^{2}x}}}$	$\,{\frac {1}{\operatorname {tg} x}}$	$\,\operatorname {ctg} x$	$\,{\frac {1}{\sqrt {\sec ^{2}x-1}}}$	$\,{\sqrt {\operatorname {cosec} ^{2}x-1}}$
$\,\sec x=$	$\,{\frac {1}{\sqrt {1-\sin ^{2}x}}}$	$\,{\frac {1}{\cos x}}$	$\,{\sqrt {1+\operatorname {tg} ^{2}x}}$	$\,{\frac {\sqrt {\operatorname {ctg} ^{2}x+1}}{\operatorname {ctg} x}}$	$\,\sec x$	$\,{\frac {\operatorname {cosec} x}{\sqrt {\operatorname {cosec} ^{2}x-1}}}$
$\,\operatorname {cosec} x=$	$\,{\frac {1}{\sin x}}$	$\,{\frac {1}{\sqrt {1-\cos ^{2}x}}}$	$\,{\frac {\sqrt {1+\operatorname {tg} ^{2}x}}{\operatorname {tg} x}}$	$\,{\sqrt {\operatorname {ctg} ^{2}x+1}}$	$\,{\frac {\sec x}{\sqrt {\sec ^{2}x-1}}}$	$\,\operatorname {cosec} x$