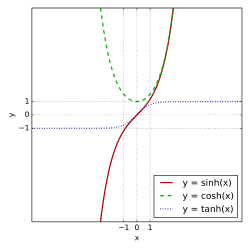
Sinh (röd), cosh (grön) och tanh (blå). Koppling mellan hyperbler och de hyperboliska funktionerna. Varje punkt på högra delen av hyperbeln har koordinaten (cosh a, sinh a) där a är dubbla rödmarkerade arean i figuren. Inom matematiken är de hyperboliska funktionerna nära besläktade med de trigonometriska funktionerna , vilket antyds av deras benämningar:
sinus hyperbolicus (sinh) cosinus hyperbolicus (cosh) tangens hyperbolicus (tanh) secans hyperbolicus (sech) cosecans hyperbolicus (csch) cotangens hyperbolicus (coth) sech och csch används sällan.
De hyperboliska funktionernas definitioner är
sinh x = e x − e − x 2 {\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}} cosh x = e x + e − x 2 {\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}} tanh x = sinh x cosh x = e x − e − x e x + e − x {\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}} sech ( x ) = 1 cosh x = 2 e x + e − x {\displaystyle \operatorname {sech} (x)={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}} csch ( x ) = 1 sinh x = 2 e x − e − x {\displaystyle \operatorname {csch} (x)={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}} coth x = 1 tanh x = e x + e − x e x − e − x {\displaystyle \coth x={\frac {1}{\tanh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}} Vid jämförelse med Eulers formler , framgår att enligt definitionerna av cosh och cos är skillnaden att vinkeln är multiplicerad med komplexa enheten i ; motsvarande gäller för sin och sinh:
cosh ( x ) = cos ( i x ) , cosh ( i x ) = cos ( x ) {\displaystyle \cosh(x)=\cos(ix),\qquad \cosh(ix)=\cos(x)} sinh ( x ) = − i sin ( i x ) , sinh ( i x ) = i sin ( x ) {\displaystyle \sinh(x)=-i\sin(ix),\qquad \sinh(ix)=i\sin(x)} och därmed kan de trigonometriska funktionerna – ur ett analytiskt perspektiv – betraktas som utvidgningar av de hyperboliska funktionerna till det komplexa talplanet . Ur ett geometriskt perspektiv är dock de trigonometriska funktionerna mer grundläggande och man kan då – ur denna synvinkel – betrakta de hyperboliska funktionerna som utvidgningar till det komplexa talplanet av trigonometriska funktioner.
Utveckling av sinh och cosh i en taylorserie kan göras med hjälp av serieutvecklingar av exponentialfunktionen :
sinh ( x ) = ∑ k = 0 ∞ x 2 k + 1 ( 2 k + 1 ) ! cosh ( x ) = ∑ k = 0 ∞ x 2 k ( 2 k ) ! {\displaystyle \sinh(x)=\sum _{k=0}^{\infty }{\frac {x^{2k+1}}{(2k+1)!}}\qquad \cosh(x)=\sum _{k=0}^{\infty }{\frac {x^{2k}}{(2k)!}}} Motsvarigheten till trigonometriska ettan , kallad hyperboliska ettan:
cosh 2 x − sinh 2 x = 1 {\displaystyle \cosh ^{2}x-\sinh ^{2}x=1} sinh är udda , cosh är jämn :
cosh ( − x ) = cosh x {\displaystyle \cosh(-x)=\cosh x} sinh ( − x ) = − sinh x {\displaystyle \sinh(-x)=-\sinh x} Summor:
sinh ( x + y ) = sinh ( x ) ⋅ cosh ( y ) + cosh ( x ) ⋅ sinh ( y ) {\displaystyle \sinh {(x+y)}=\sinh {(x)}\cdot \cosh {(y)}+\cosh {(x)}\cdot \sinh {(y)}} sinh ( x − y ) = sinh ( x ) ⋅ cosh ( y ) − cosh ( x ) ⋅ sinh ( y ) {\displaystyle \sinh {(x-y)}=\sinh {(x)}\cdot \cosh {(y)}-\cosh {(x)}\cdot \sinh {(y)}} cosh ( x + y ) = cosh ( x ) ⋅ cosh ( y ) + sinh ( x ) ⋅ sinh ( y ) {\displaystyle \cosh {(x+y)}=\cosh {(x)}\cdot \cosh {(y)}+\sinh {(x)}\cdot \sinh {(y)}} cosh ( x − y ) = cosh ( x ) ⋅ cosh ( y ) − sinh ( x ) ⋅ sinh ( y ) {\displaystyle \cosh {(x-y)}=\cosh {(x)}\cdot \cosh {(y)}-\sinh {(x)}\cdot \sinh {(y)}} De hyperboliska funktionernas inverser benämns area hyperbolicus eller arcus hyperbolicus . Dock kan varje sådan invers-funktion skrivas med hjälp av logaritmer :
arcsinh x = ln ( x + x 2 + 1 ) {\displaystyle \operatorname {arcsinh} x=\ln(x+{\sqrt {x^{2}+1}})} arccosh x = ln ( x + x 2 − 1 ) {\displaystyle \operatorname {arccosh} x=\ln(x+{\sqrt {x^{2}-1}})} arctanh x = 1 2 ⋅ ln ( 1 + x 1 − x ) {\displaystyle \operatorname {arctanh} x={\frac {1}{2}}\cdot \ln \left({\frac {1+x}{1-x}}\right)} Speciellt gäller att arcsinh är entydigt definierad för hela ℝ till skillnad från inverserna av de trigonometriska funktionerna där man undviker flertydighet genom att införa begreppet principalvärde .
d d x sinh ( x ) = cosh ( x ) {\displaystyle {\frac {d}{dx}}\sinh(x)=\cosh(x)\,} d d x cosh ( x ) = sinh ( x ) {\displaystyle {\frac {d}{dx}}\cosh(x)=\sinh(x)\,} d d x tanh ( x ) = 1 − tanh 2 ( x ) {\displaystyle {\frac {d}{dx}}\tanh(x)=1-\tanh ^{2}(x)\,} d d x coth ( x ) = 1 − coth 2 ( x ) {\displaystyle {\frac {d}{dx}}\coth(x)=1-\coth ^{2}(x)\,} d d x csch(x) = − coth ( x ) csch(x) {\displaystyle {\frac {d}{dx}}\ {\hbox{csch(x)}}=-\coth(x)\ {\hbox{csch(x)}}\,} d d x sech(x) = − tanh ( x ) sech(x) {\displaystyle {\frac {d}{dx}}\ {\hbox{sech(x)}}=-\tanh(x)\ {\hbox{sech(x)}}\,} d d x arcsinh ( x ) = 1 x 2 + 1 {\displaystyle {\frac {d}{dx}}\operatorname {arcsinh} (x)={\frac {1}{\sqrt {x^{2}+1}}}} d d x arccosh ( x ) = 1 x 2 − 1 {\displaystyle {\frac {d}{dx}}\operatorname {arccosh} (x)={\frac {1}{\sqrt {x^{2}-1}}}} d d x arctanh ( x ) = 1 1 − x 2 {\displaystyle {\frac {d}{dx}}\operatorname {arctanh} (x)={\frac {1}{1-x^{2}}}} d d x arccsch ( x ) = − 1 | x | 1 + x 2 {\displaystyle {\frac {d}{dx}}\operatorname {arccsch} (x)=-{\frac {1}{\left|x\right|{\sqrt {1+x^{2}}}}}} d d x arcsech ( x ) = − 1 x 1 − x 2 {\displaystyle {\frac {d}{dx}}\operatorname {arcsech} (x)=-{\frac {1}{x{\sqrt {1-x^{2}}}}}} d d x arccoth ( x ) = 1 1 − x 2 {\displaystyle {\frac {d}{dx}}\operatorname {arccoth} (x)={\frac {1}{1-x^{2}}}} Hyperbolisk funktion .GonioLab : Visualisering av enhetscirkeln, trigonometriska och hyperboliska funktioner (Java Web Start)

 Wikimedia Commons har media som rör Hyperbolisk funktion.
Wikimedia Commons har media som rör Hyperbolisk funktion.





























