Акустичний резонанс

Акустичний резонанс — явище, внаслідок якого акустична система підсилює ті звукові хвилі, частота яких відповідає одній із власних природних частот (резонансних частот) коливань.

Термін «акустичний резонанс» іноді використовується для звуження поняття механічного резонансу^[en] до частотного діапазону слуху людини, але оскільки акустика розглядає поширення коливань у речовині в цілому,^[1] акустичний резонанс може виникати на частотах поза діапазоном слуху людини.

Акустично-резонансний об'єкт зазвичай має більше однієї резонансної частоти, особливо в гармоніках найсильнішого резонансу. Він легко вібрує на цих частотах і слабше вібрує на інших частотах. Він «вибере» свою резонансну частоту із складного збудження, наприклад, поштовху чи широкосмугового шуму. По суті, він фільтрує всі частоти, окрім своєї резонансної.

Акустичний резонанс є важливим фактором для майстрів з виготовлення музичних інструментів, оскільки більшість акустичних інструментів використовують резонатори, такі як струни та тіло скрипки, трубка певної довжини у флейті та барабанна мембрана. Акустичний резонанс також важливий для слуху. Наприклад, резонанс жорсткого структурного елемента, всередині кохлеї внутрішнього вуха, який називається базилярною мембраною^[en], дозволяє волосковим клітинам на мембрані виявляти звук. У ссавців мембрана звужується вздовж завитка, так що високі частоти спричиняють резонанс на одному кінці, а низькі — на іншому.

У музичних інструментах (лютні, арфі, гітарі, фортепіано, скрипці тощо), натягнуті струни мають резонансні частоти безпосередньо пов'язані з масою, довжиною та силою натягу струни. Довжина хвилі, яка викличе перший резонанс у струні, дорівнює подвоєній довжині струни. Вищі резонанси відповідають довжинам хвиль, які дорівнюють поділеній націло довжині основної хвилі. Відповідні частоти пов'язані зі швидкістю ${\displaystyle v}$ хвилі, що рухається вздовж струни, описуються формулою

${\displaystyle f={nv \over 2L}}$

де L — довжина струни (для струни, закріпленої на обох кінцях) і n = 1, 2, 3… (гармоніка на відкритому кінці труби (тобто обидва кінці труби відкриті)). Швидкість хвилі у струні або дроті пов'язана з її натягом T і масою на одиницю довжини ρ:

${\displaystyle v={\sqrt {T \over \rho }}}$

Тож частота пов'язана з властивостями струни рівнянням

${\displaystyle f={n{\sqrt {T \over \rho }} \over 2L}={n{\sqrt {T \over m/L}} \over 2L}}$

де T — напруга, ρ — маса на одиницю довжини, а m — загальна маса.

Більший натяг і менша довжина спричиняють збільшення резонансних частот. Коли струна збуджується поштовхом (смикання пальцем або удар молоточком), струна вібрує на всіх частотах, наявних в імпульсі (поштовх, теоретично, містить «всі» частоти). Ті частоти, які не є однією з резонансних, швидко відфільтровуються — вони ослаблюються — і все, що залишилося, — це гармонійні вібрації, які ми чуємо як музичну ноту.

Резонанс струни виникає в струнних інструментах. Струни або частини струн можуть резонувати на своїй основній або обертоновій частоті, коли звучать інші струни. Наприклад, струна A з частотою 440 Гц спричинить резонанс струни E з частотою 330 Гц, тому що вони поділяють обертон 1320 Гц (3-й обертон A та 4-й обертон E).

Резонанс повітряного стовпа пов'язаний із довжиною труби, її формою та чи має вона закриті чи відкриті кінці. Музично корисні форми труб конічні та циліндричні (див. Канал^[en]). Кажуть, що труба закрита, якщо в ній закрито один з кінців, і відкрита, коли відкриті обидва кінці. Сучасні оркестрові флейти поводяться як відкриті циліндричні труби; кларнети та амбушурні (мідні) інструменти — як закриті циліндричні труби; і саксофони, гобої та фаготи діють як закриті конічні труби.^[2] Вібраційні повітряні стовпи також мають резонанс на гармоніках, як і струнні.

Будь-який циліндр резонує на декількох частотах, створюючи кілька музичних частот. Найнижча частота називається основною частотою або першою гармонікою. Циліндри, що використовуються як музичні інструменти, як правило, відкриті або на обох кінцях, як на флейті, або на одному кінці, як у деяких органних труб. Однак циліндр, закритий на обох кінцях, також може бути використаний для створення або виявлення звукових хвиль, як у трубі Рубенса.

Резонансні властивості циліндра можна зрозуміти, враховуючи поведінку звукової хвилі у повітрі. Звук рухається як поздовжня хвиля стиснення, внаслідок чого молекули повітря рухаються вперед-назад вздовж напрямку руху. Усередині труби утворюється стояча хвиля, довжина хвилі якої залежить від довжини труби. На закритому кінці труби молекули повітря не можуть вільно рухатися, тому цей кінець труби є вузлом^[en] стоячої хвилі. На відкритому кінці труби молекули повітря можуть вільно рухатися, формуючи пучність зміщення. Там, де молекули не здатні вільно рухатися, тиск зростає. Таким чином, закритий кінець труби — це напірний вузол, а також пучність зміщення.

У таблиці нижче показані хвилі переміщення в циліндрі, закритому на обох кінцях. Зауважте, що молекули повітря поблизу закритих кінців не можуть рухатися, тоді як молекули біля центру труби рухаються вільно. У першій гармоніці, закрита труба містить рівно половину стоячої хвилі (вузол-пучність-вузол).

Частота	Порядок	Назва 1	Назва 2	Назва 3	Коливання струни	Коливання повітря
1 · f =    440 Гц	n = 1	1-а частина	основний тон	1-а гармоніка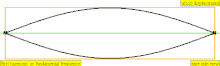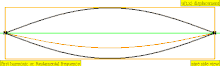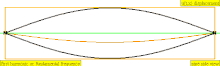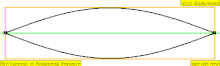
2 · f =    880 Гц	n = 2	2-і частини	1-й обертон	2-а гармоніка
3 · f = 1320 Гц	n = 3	3-и частини	2-й обертон	3-я гармоніка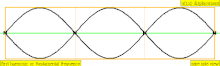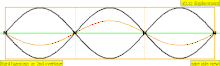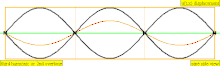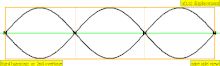
4 · f = 1760 Гц	n = 4	4-и частини	3-й обертон	4-а гармоніка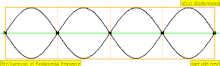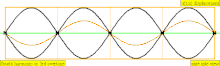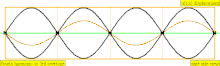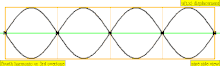

У циліндрах з обома відкритими кінцями, молекули повітря біля кінця вільно переміщуються всередину та за межі труби. Цей рух спричиняє витіснення пучностей стоячої хвилі. Вузли, як правило, утворюються всередині циліндра, подалі від кінців. На першій гармоніці відкрита труба містить рівно половину стоячої хвилі (пучність-вузол-пучність). Таким чином, гармоніки відкритого циліндра обчислюються так само, як гармоніки закритого з двох боків циліндра.

Передуваючи^[en] відкриту трубу, можна отримати ноту, яка на октаву вища від основної частоти або ноти труби. Наприклад, якщо основна нота відкритої труби дорівнює C1, то передування труби дає С2, що на октаву вище від С1.^[3]

${\displaystyle f={nv \over 2L}}$

де n — ціле натуральне число (1, 2, 3…), що представляє резонансний вузол, L — довжина трубки, v — швидкість звуку в повітрі (яка становить приблизно 343 м/с (1230 км/год) при 20 °C).

Більш точне рівняння з урахуванням кінцевої поправки^[en] наведено нижче:

${\displaystyle f={nv \over 2(L+0.8d)}}$

де d — діаметр резонансної труби. Це рівняння компенсує той факт, що точна точка, в якій звукова хвиля відбивається на відкритому кінці, знаходиться не точно на кінцевій ділянці трубки, а на невеликій відстані поза трубою.

Коефіцієнт відбиття трохи менший від 1; відкритий кінець поводиться не як нескінченно малий акустичний імпеданс; скоріше, він має скінченне значення, яке називається радіаційним імпедансом, яке залежить від діаметра трубки, довжини хвилі та типу відбивної дошки, можливо, наявної навколо отвору трубки.

Отже, коли n дорівнює 1:

${\displaystyle f={v \over 2(L+0.8d)}}$

${\displaystyle {f(2(L+0.8d))}=v}$

${\displaystyle {f\lambda }=v}$

${\displaystyle \lambda ={2(L+0.8d)}}$

де v — швидкість звуку, L — довжина резонансної трубки, d — діаметр трубки, f — резонансна частота звуку, а λ — резонансна довжина хвилі.

При використанні в органі труба, закрита на одному кінці, називається «заглушеною трубою». Такі циліндри мають основну частоту, але їх можна перекрити, щоб створити вищі частоти або ноти. Ці перекриті регістри можна налаштувати за допомогою різної конусності. Заглушена труба резонує на такій самій основній частоті, що й відкрита труба вдвічі більшої довжини, довжина хвилі дорівнює її довжині, помноженій на 4. У заглушеній трубі вузол зміщення або точка без вібрації завжди з'являється на закритому кінці, і, якщо трубка резонує, вона матиме пучність або найбільшу вібрацію в точці Фі (довжина × 0,618) поблизу відкритого кінця.

Передуваючи циліндричну заглушену трубу, можна отримати ноту, яка приблизно на дванадцять ступенів вища від основної ноти труби. Іноді це описують як п'ятий ступінь понад октаву від основної ноти. Наприклад, якщо основна нота закритої труби — це С1, то при передуванні труби виходить G2, що на дванадцяту ступенів вище від C1, або на п'ять ступенів вище від C2. Зменшення конусності цього циліндра дозволяє налаштувати другу гармоніку передутої ноти близько до октавної позиції або 8 го ступеня.^[4] Відкриття невеликого «голосового отвору» в точці фі виключить основну частоту і змусить трубку резонувати на 12-му ступені вище основної ноти. Цей прийом використовується у блокфлейті, коли відкривається отвір для великого пальця. Переміщення цього маленького отвору вгору, ближче до виходу звуку, зробить її «ехо-отвором» (модифікація блокфлейти Долмеча^[ru]), який при відкритті дасть точну половину ноти вище від основної. Примітка: для точної половини частоти ноти потрібна невелика корекція розміру або діаметра.^[3]

Заглушена труба матиме приблизні резонанси:

${\displaystyle f={nv \over 4L}}$

де n — непарне число (1, 3, 5…). Цей тип трубки виробляє лише непарні гармоніки і має свою основну частоту на октаву нижче, ніж у відкритого циліндра (тобто половину частоти).

Більш точне рівняння:

${\displaystyle f={nv \over 4(L+0.4d)}}$.

Знову ж таки, коли n дорівнює 1:

${\displaystyle f={v \over 4(L+0.4d)}}$

${\displaystyle {f(4(L+0.4d))}=v}$

${\displaystyle {f\lambda }=v}$

${\displaystyle \lambda ={4(L+0.4d)}}$

Резонансна частота жорсткої порожнини статичного об'єму V ₀ із витягнутим звуковим отвором площею А та довжиною L визначається за формулою резонансу Гельмгольца^[5][6]

На двох діаграмах, наведених нижче, показані перші три резонанси хвилі тиску в циліндричній трубі, з пучностями на закритому кінці труби. На схемі 1 труба відкрита з обох кінців. На схемі 2 вона закрита на одному кінці. Горизонтальна вісь — це тиск. Зауважте, що в цьому випадку відкритий кінець труби є вузлом тиску, тоді як закритий кінець — пучністю тиску.

Відкрита конічна труба, тобто, у формі зрізаного конуса з обома відкритими кінцями, матиме резонансні частоти приблизно рівні таким у відкритої циліндричної труби такої ж довжини.

Резонансні частоти заглушеної конусоподібної трубки — повного конуса або зрізаного з одним закритим кінцем — відповідають більш складним умовам:

${\displaystyle kL=n\pi -\tan ^{-1}kx}$

де хвильове число k

${\displaystyle k=2\pi f/v}$

і x — відстань від малого кінця зрізаного конуса до вершини. Коли х мале, тобто коли конус майже цілий, це набуває вигляду

${\displaystyle k(L+x)\approx n\pi }$

що веде до резонансних частот, приблизно рівних частотам відкритого циліндра, довжина якого L + х. Словом, повна конічна труба поводиться приблизно як відкрита циліндрична труба такої ж довжини, і для першого порядку поведінка не змінюється, якщо повний конус буде замінений закритим закритим відрізком цього конуса.

Звукові хвилі у прямокутному ящику спостерігаються в корпусах гучномовців та будівлях. Прямокутна будівля має резонанси, які називають кімнатними модами^[en]. Для прямокутного ящика резонансні частоти задаються формулою^[7]

${\displaystyle f={v \over 2}{\sqrt {\left({\ell \over L_{x}}\right)^{2}+\left({m \over L_{y}}\right)^{2}+\left({n \over L_{z}}\right)^{2}}}}$

де v — швидкість звуку, L_x, L_y і L _z — розміри ящика. ${\displaystyle \ell }$, ${\displaystyle m}$, і ${\displaystyle n}$ — це невід'ємні цілі числа, які не можуть бути всі разом нулями. Якщо малий корпус гучномовця є повітронепроникним, частота досить низька і стиснення досить високе, звуковий тиск (рівень у децибелах) всередині коробки буде однаковим у будь-якому місці (гідравлічний тиск).

${\displaystyle f={\frac {v}{2\pi }}{\sqrt {\frac {A}{V_{0}L_{eq}}}}}$

де ${\displaystyle L_{eq}}$ — еквівалентна довжина горловини з кінцевою поправкою

${\displaystyle L_{eq}=L+0.75d}$ для безфланцевої горловини^[8]

${\displaystyle L_{eq}=L+0.85d}$ для фланцевої горловини

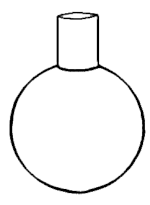
Для сферичної порожнини формула резонансної частоти набуває вигляду

${\displaystyle f={\frac {vd}{\pi }}{\sqrt {\frac {3}{8L_{eq}D^{3}}}}}$

де

D — діаметр сфери

d — діаметр звукового отвору

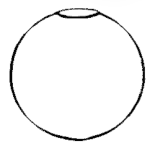
Для сфери з простим звуковим отвором L = 0 і поверхня сфери виконує роль фланця, отже

${\displaystyle f={\frac {v}{\pi }}{\sqrt {\frac {3d}{8(0.85)D^{3}}}}}$

В сухому повітрі при 20 °C, з d і D в метрах, f у герцах, маємо

${\displaystyle f=72.6{\sqrt {\frac {d}{D^{3}}}}}$

Деякі великі конічні інструменти, такі як туби, мають сильний і корисний резонанс, якого немає у відомому гармонічному ряду. Наприклад, більшість туб B♭ мають сильний резонанс на низькій E♭ (E♭1, 39 Гц), що знаходиться між основним тоном і другою гармонікою (на октаву, вище від основного). Ці альтернативні резонанси часто відомі як хибні тони або привілейовані тони.

Найбільш переконливе пояснення наявності хибних тонів: ріг діє як «третина труби», а не як напівтруба. У розширенні залишається пучність, але тоді буде вузол на 1/3 шляху назад до мундштука. Якщо так, то, основний тон мав би втрачатись повністю, а залишились би тільки обертони. Адже вузол і пучність стикаються в одній точці і скасовують основний тон.

Це класична демонстрація резонансу. Склянка має природний резонанс, частоту, на якій скло легко вібрує. Тому склянку потрібно рухати звуковою хвилею з такою частотою. Якщо сила від звукової хвилі, що змушує склянку вібрувати, досить велика, розмір вібрації стане настільки великим, що склянка трісне. Щоб зробити це надійно для наукової демонстрації, потрібна практика і ретельний вибір склянки й гучномовця.^[9]

Кілька композиторів зробили резонанс предметом композицій. Ельвін Люсьєр використовував акустичні інструменти та генератори синусоїди для дослідження резонансу великих та малих предметів у багатьох своїх композиціях. Пауліна Оліверос та Стюарт Демпстер^[en] регулярно виступають у великих ревербераційних просторах, таких як цистерна на 2 млн амер. галонів (7600 м³) у Форт-Вордені^[en], штат Вашингтон, який має реверберацію тривалістю 45 секунд. Професор композиції та композитор Академії музики Мальме^[sv] Кента Олофссона створив «Терпсихорд, п'єсу для ударних та попередньо записаних звуків [де] резонанси від акустичних інструментів формують звукові мостів до заздалегідь записаних електронних звуків, що, у свою чергу, продовжують резонанси, перетворюючи їх на нові звукові жести».^[10]

• Гармонія
• Теорія музики
• Резонанс
• Реверберація

• Nederveen, Cornelis Johannes, Acoustical aspects of woodwind instruments. Amsterdam, Frits Knuf, 1969.
• Rossing, Thomas D., and Fletcher, Neville H., Principles of Vibration and Sound. New York, Springer-Verlag, 1995.

• Аплет стоячих хвиль [Архівовано 9 грудня 2019 у Wayback Machine.]