Equalities that involve trigonometric functions
In trigonometry , trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involving certain functions of one or more angles . They are distinct from triangle identities , which are identities potentially involving angles but also involving side lengths or other lengths of a triangle .
These identities are useful whenever expressions involving trigonometric functions need to be simplified. An important application is the integration of non-trigonometric functions: a common technique involves first using the substitution rule with a trigonometric function , and then simplifying the resulting integral with a trigonometric identity.
Pythagorean identities [ edit ] Trigonometric functions and their reciprocals on the unit circle. All of the right-angled triangles are similar, i.e. the ratios between their corresponding sides are the same. For sin, cos and tan the unit-length radius forms the hypotenuse of the triangle that defines them. The reciprocal identities arise as ratios of sides in the triangles where this unit line is no longer the hypotenuse. The triangle shaded blue illustrates the identity 1 + cot 2 θ = csc 2 θ {\displaystyle 1+\cot ^{2}\theta =\csc ^{2}\theta } tan 2 θ + 1 = sec 2 θ {\displaystyle \tan ^{2}\theta +1=\sec ^{2}\theta } The basic relationship between the sine and cosine is given by the Pythagorean identity:
sin 2 θ + cos 2 θ = 1 , {\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1,}
where sin 2 θ {\displaystyle \sin ^{2}\theta } ( sin θ ) 2 {\displaystyle (\sin \theta )^{2}} cos 2 θ {\displaystyle \cos ^{2}\theta } ( cos θ ) 2 . {\displaystyle (\cos \theta )^{2}.}
This can be viewed as a version of the Pythagorean theorem , and follows from the equation x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1} unit circle . This equation can be solved for either the sine or the cosine:
sin θ = ± 1 − cos 2 θ , cos θ = ± 1 − sin 2 θ . {\displaystyle {\begin{aligned}\sin \theta &=\pm {\sqrt {1-\cos ^{2}\theta }},\\\cos \theta &=\pm {\sqrt {1-\sin ^{2}\theta }}.\end{aligned}}}
where the sign depends on the quadrant of θ . {\displaystyle \theta .}
Dividing this identity by sin 2 θ {\displaystyle \sin ^{2}\theta } cos 2 θ {\displaystyle \cos ^{2}\theta } 1 + cot 2 θ = csc 2 θ 1 + tan 2 θ = sec 2 θ sec 2 θ + csc 2 θ = sec 2 θ csc 2 θ {\displaystyle {\begin{aligned}&1+\cot ^{2}\theta =\csc ^{2}\theta \\&1+\tan ^{2}\theta =\sec ^{2}\theta \\&\sec ^{2}\theta +\csc ^{2}\theta =\sec ^{2}\theta \csc ^{2}\theta \end{aligned}}}
Using these identities, it is possible to express any trigonometric function in terms of any other (up to a plus or minus sign):
Each trigonometric function in terms of each of the other five.[ 1] in terms of sin θ {\displaystyle \sin \theta } csc θ {\displaystyle \csc \theta } cos θ {\displaystyle \cos \theta } sec θ {\displaystyle \sec \theta } tan θ {\displaystyle \tan \theta } cot θ {\displaystyle \cot \theta } sin θ = {\displaystyle \sin \theta =} sin θ {\displaystyle \sin \theta } 1 csc θ {\displaystyle {\frac {1}{\csc \theta }}} ± 1 − cos 2 θ {\displaystyle \pm {\sqrt {1-\cos ^{2}\theta }}} ± sec 2 θ − 1 sec θ {\displaystyle \pm {\frac {\sqrt {\sec ^{2}\theta -1}}{\sec \theta }}} ± tan θ 1 + tan 2 θ {\displaystyle \pm {\frac {\tan \theta }{\sqrt {1+\tan ^{2}\theta }}}} ± 1 1 + cot 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1+\cot ^{2}\theta }}}} csc θ = {\displaystyle \csc \theta =} 1 sin θ {\displaystyle {\frac {1}{\sin \theta }}} csc θ {\displaystyle \csc \theta } ± 1 1 − cos 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1-\cos ^{2}\theta }}}} ± sec θ sec 2 θ − 1 {\displaystyle \pm {\frac {\sec \theta }{\sqrt {\sec ^{2}\theta -1}}}} ± 1 + tan 2 θ tan θ {\displaystyle \pm {\frac {\sqrt {1+\tan ^{2}\theta }}{\tan \theta }}} ± 1 + cot 2 θ {\displaystyle \pm {\sqrt {1+\cot ^{2}\theta }}} cos θ = {\displaystyle \cos \theta =} ± 1 − sin 2 θ {\displaystyle \pm {\sqrt {1-\sin ^{2}\theta }}} ± csc 2 θ − 1 csc θ {\displaystyle \pm {\frac {\sqrt {\csc ^{2}\theta -1}}{\csc \theta }}} cos θ {\displaystyle \cos \theta } 1 sec θ {\displaystyle {\frac {1}{\sec \theta }}} ± 1 1 + tan 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1+\tan ^{2}\theta }}}} ± cot θ 1 + cot 2 θ {\displaystyle \pm {\frac {\cot \theta }{\sqrt {1+\cot ^{2}\theta }}}} sec θ = {\displaystyle \sec \theta =} ± 1 1 − sin 2 θ {\displaystyle \pm {\frac {1}{\sqrt {1-\sin ^{2}\theta }}}} ± csc θ csc 2 θ − 1 {\displaystyle \pm {\frac {\csc \theta }{\sqrt {\csc ^{2}\theta -1}}}} 1 cos θ {\displaystyle {\frac {1}{\cos \theta }}} sec θ {\displaystyle \sec \theta } ± 1 + tan 2 θ {\displaystyle \pm {\sqrt {1+\tan ^{2}\theta }}} ± 1 + cot 2 θ cot θ {\displaystyle \pm {\frac {\sqrt {1+\cot ^{2}\theta }}{\cot \theta }}} tan θ = {\displaystyle \tan \theta =} ± sin θ 1 − sin 2 θ {\displaystyle \pm {\frac {\sin \theta }{\sqrt {1-\sin ^{2}\theta }}}} ± 1 csc 2 θ − 1 {\displaystyle \pm {\frac {1}{\sqrt {\csc ^{2}\theta -1}}}} ± 1 − cos 2 θ cos θ {\displaystyle \pm {\frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta }}} ± sec 2 θ − 1 {\displaystyle \pm {\sqrt {\sec ^{2}\theta -1}}} tan θ {\displaystyle \tan \theta } 1 cot θ {\displaystyle {\frac {1}{\cot \theta }}} cot θ = {\displaystyle \cot \theta =} ± 1 − sin 2 θ sin θ {\displaystyle \pm {\frac {\sqrt {1-\sin ^{2}\theta }}{\sin \theta }}} ± csc 2 θ − 1 {\displaystyle \pm {\sqrt {\csc ^{2}\theta -1}}} ± cos θ 1 − cos 2 θ {\displaystyle \pm {\frac {\cos \theta }{\sqrt {1-\cos ^{2}\theta }}}} ± 1 sec 2 θ − 1 {\displaystyle \pm {\frac {1}{\sqrt {\sec ^{2}\theta -1}}}} 1 tan θ {\displaystyle {\frac {1}{\tan \theta }}} cot θ {\displaystyle \cot \theta }
[ edit ] By examining the unit circle, one can establish the following properties of the trigonometric functions.
Transformation of coordinates (a ,b ) when shifting the reflection angle α {\displaystyle \alpha } π 4 {\displaystyle {\frac {\pi }{4}}} When the direction of a Euclidean vector is represented by an angle θ , {\displaystyle \theta ,} x {\displaystyle x} x {\displaystyle x} θ {\displaystyle \theta } α , {\displaystyle \alpha ,} θ ′ {\displaystyle \theta ^{\prime }} θ ′ = 2 α − θ . {\displaystyle \theta ^{\prime }=2\alpha -\theta .}
The values of the trigonometric functions of these angles θ , θ ′ {\displaystyle \theta ,\;\theta ^{\prime }} α {\displaystyle \alpha } reduction formulae .[ 2]
θ {\displaystyle \theta } α = 0 {\displaystyle \alpha =0} [ 3] odd/even identities θ {\displaystyle \theta } α = π 4 {\displaystyle \alpha ={\frac {\pi }{4}}} θ {\displaystyle \theta } α = π 2 {\displaystyle \alpha ={\frac {\pi }{2}}} θ {\displaystyle \theta } α = 3 π 4 {\displaystyle \alpha ={\frac {3\pi }{4}}} θ {\displaystyle \theta } α = π {\displaystyle \alpha =\pi } compare to α = 0 {\displaystyle \alpha =0} sin ( − θ ) = − sin θ {\displaystyle \sin(-\theta )=-\sin \theta } sin ( π 2 − θ ) = cos θ {\displaystyle \sin \left({\tfrac {\pi }{2}}-\theta \right)=\cos \theta } sin ( π − θ ) = + sin θ {\displaystyle \sin(\pi -\theta )=+\sin \theta } sin ( 3 π 2 − θ ) = − cos θ {\displaystyle \sin \left({\tfrac {3\pi }{2}}-\theta \right)=-\cos \theta } sin ( 2 π − θ ) = − sin ( θ ) = sin ( − θ ) {\displaystyle \sin(2\pi -\theta )=-\sin(\theta )=\sin(-\theta )} cos ( − θ ) = + cos θ {\displaystyle \cos(-\theta )=+\cos \theta } cos ( π 2 − θ ) = sin θ {\displaystyle \cos \left({\tfrac {\pi }{2}}-\theta \right)=\sin \theta } cos ( π − θ ) = − cos θ {\displaystyle \cos(\pi -\theta )=-\cos \theta } cos ( 3 π 2 − θ ) = − sin θ {\displaystyle \cos \left({\tfrac {3\pi }{2}}-\theta \right)=-\sin \theta } cos ( 2 π − θ ) = + cos ( θ ) = cos ( − θ ) {\displaystyle \cos(2\pi -\theta )=+\cos(\theta )=\cos(-\theta )} tan ( − θ ) = − tan θ {\displaystyle \tan(-\theta )=-\tan \theta } tan ( π 2 − θ ) = cot θ {\displaystyle \tan \left({\tfrac {\pi }{2}}-\theta \right)=\cot \theta } tan ( π − θ ) = − tan θ {\displaystyle \tan(\pi -\theta )=-\tan \theta } tan ( 3 π 2 − θ ) = + cot θ {\displaystyle \tan \left({\tfrac {3\pi }{2}}-\theta \right)=+\cot \theta } tan ( 2 π − θ ) = − tan ( θ ) = tan ( − θ ) {\displaystyle \tan(2\pi -\theta )=-\tan(\theta )=\tan(-\theta )} csc ( − θ ) = − csc θ {\displaystyle \csc(-\theta )=-\csc \theta } csc ( π 2 − θ ) = sec θ {\displaystyle \csc \left({\tfrac {\pi }{2}}-\theta \right)=\sec \theta } csc ( π − θ ) = + csc θ {\displaystyle \csc(\pi -\theta )=+\csc \theta } csc ( 3 π 2 − θ ) = − sec θ {\displaystyle \csc \left({\tfrac {3\pi }{2}}-\theta \right)=-\sec \theta } csc ( 2 π − θ ) = − csc ( θ ) = csc ( − θ ) {\displaystyle \csc(2\pi -\theta )=-\csc(\theta )=\csc(-\theta )} sec ( − θ ) = + sec θ {\displaystyle \sec(-\theta )=+\sec \theta } sec ( π 2 − θ ) = csc θ {\displaystyle \sec \left({\tfrac {\pi }{2}}-\theta \right)=\csc \theta } sec ( π − θ ) = − sec θ {\displaystyle \sec(\pi -\theta )=-\sec \theta } sec ( 3 π 2 − θ ) = − csc θ {\displaystyle \sec \left({\tfrac {3\pi }{2}}-\theta \right)=-\csc \theta } sec ( 2 π − θ ) = + sec ( θ ) = sec ( − θ ) {\displaystyle \sec(2\pi -\theta )=+\sec(\theta )=\sec(-\theta )} cot ( − θ ) = − cot θ {\displaystyle \cot(-\theta )=-\cot \theta } cot ( π 2 − θ ) = tan θ {\displaystyle \cot \left({\tfrac {\pi }{2}}-\theta \right)=\tan \theta } cot ( π − θ ) = − cot θ {\displaystyle \cot(\pi -\theta )=-\cot \theta } cot ( 3 π 2 − θ ) = + tan θ {\displaystyle \cot \left({\tfrac {3\pi }{2}}-\theta \right)=+\tan \theta } cot ( 2 π − θ ) = − cot ( θ ) = cot ( − θ ) {\displaystyle \cot(2\pi -\theta )=-\cot(\theta )=\cot(-\theta )}
Shifts and periodicity [ edit ] Transformation of coordinates (a ,b ) when shifting the angle θ {\displaystyle \theta } π 2 {\displaystyle {\frac {\pi }{2}}} Shift by one quarter period Shift by one half period Shift by full periods[ 4] Period sin ( θ ± π 2 ) = ± cos θ {\displaystyle \sin(\theta \pm {\tfrac {\pi }{2}})=\pm \cos \theta } sin ( θ + π ) = − sin θ {\displaystyle \sin(\theta +\pi )=-\sin \theta } sin ( θ + k ⋅ 2 π ) = + sin θ {\displaystyle \sin(\theta +k\cdot 2\pi )=+\sin \theta } 2 π {\displaystyle 2\pi } cos ( θ ± π 2 ) = ∓ sin θ {\displaystyle \cos(\theta \pm {\tfrac {\pi }{2}})=\mp \sin \theta } cos ( θ + π ) = − cos θ {\displaystyle \cos(\theta +\pi )=-\cos \theta } cos ( θ + k ⋅ 2 π ) = + cos θ {\displaystyle \cos(\theta +k\cdot 2\pi )=+\cos \theta } 2 π {\displaystyle 2\pi } csc ( θ ± π 2 ) = ± sec θ {\displaystyle \csc(\theta \pm {\tfrac {\pi }{2}})=\pm \sec \theta } csc ( θ + π ) = − csc θ {\displaystyle \csc(\theta +\pi )=-\csc \theta } csc ( θ + k ⋅ 2 π ) = + csc θ {\displaystyle \csc(\theta +k\cdot 2\pi )=+\csc \theta } 2 π {\displaystyle 2\pi } sec ( θ ± π 2 ) = ∓ csc θ {\displaystyle \sec(\theta \pm {\tfrac {\pi }{2}})=\mp \csc \theta } sec ( θ + π ) = − sec θ {\displaystyle \sec(\theta +\pi )=-\sec \theta } sec ( θ + k ⋅ 2 π ) = + sec θ {\displaystyle \sec(\theta +k\cdot 2\pi )=+\sec \theta } 2 π {\displaystyle 2\pi } tan ( θ ± π 4 ) = tan θ ± 1 1 ∓ tan θ {\displaystyle \tan(\theta \pm {\tfrac {\pi }{4}})={\tfrac {\tan \theta \pm 1}{1\mp \tan \theta }}} tan ( θ + π 2 ) = − cot θ {\displaystyle \tan(\theta +{\tfrac {\pi }{2}})=-\cot \theta } tan ( θ + k ⋅ π ) = + tan θ {\displaystyle \tan(\theta +k\cdot \pi )=+\tan \theta } π {\displaystyle \pi } cot ( θ ± π 4 ) = cot θ ∓ 1 1 ± cot θ {\displaystyle \cot(\theta \pm {\tfrac {\pi }{4}})={\tfrac {\cot \theta \mp 1}{1\pm \cot \theta }}} cot ( θ + π 2 ) = − tan θ {\displaystyle \cot(\theta +{\tfrac {\pi }{2}})=-\tan \theta } cot ( θ + k ⋅ π ) = + cot θ {\displaystyle \cot(\theta +k\cdot \pi )=+\cot \theta } π {\displaystyle \pi }
The sign of trigonometric functions depends on quadrant of the angle. If − π < θ ≤ π {\displaystyle {-\pi }<\theta \leq \pi } sgn is the sign function ,
sgn ( sin θ ) = sgn ( csc θ ) = { + 1 if 0 < θ < π − 1 if − π < θ < 0 0 if θ ∈ { 0 , π } sgn ( cos θ ) = sgn ( sec θ ) = { + 1 if − 1 2 π < θ < 1 2 π − 1 if − π < θ < − 1 2 π or 1 2 π < θ < π 0 if θ ∈ { − 1 2 π , 1 2 π } sgn ( tan θ ) = sgn ( cot θ ) = { + 1 if − π < θ < − 1 2 π or 0 < θ < 1 2 π − 1 if − 1 2 π < θ < 0 or 1 2 π < θ < π 0 if θ ∈ { − 1 2 π , 0 , 1 2 π , π } {\displaystyle {\begin{aligned}\operatorname {sgn}(\sin \theta )=\operatorname {sgn}(\csc \theta )&={\begin{cases}+1&{\text{if}}\ \ 0<\theta <\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <0\\0&{\text{if}}\ \ \theta \in \{0,\pi \}\end{cases}}\\[5mu]\operatorname {sgn}(\cos \theta )=\operatorname {sgn}(\sec \theta )&={\begin{cases}+1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },{\tfrac {1}{2}}\pi {\bigr \}}\end{cases}}\\[5mu]\operatorname {sgn}(\tan \theta )=\operatorname {sgn}(\cot \theta )&={\begin{cases}+1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ 0<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <0\ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },0,{\tfrac {1}{2}}\pi ,\pi {\bigr \}}\end{cases}}\end{aligned}}}
The trigonometric functions are periodic with common period 2 π , {\displaystyle 2\pi ,} θ outside the interval ( − π , π ] , {\displaystyle ({-\pi },\pi ],} § Shifts and periodicity above).
Angle sum and difference identities [ edit ] Illustration of angle addition formulae for the sine and cosine of acute angles. Emphasized segment is of unit length. Diagram showing the angle difference identities for sin ( α − β ) {\displaystyle \sin(\alpha -\beta )} cos ( α − β ) {\displaystyle \cos(\alpha -\beta )} These are also known as the angle addition and subtraction theorems (or formulae ). sin ( α + β ) = sin α cos β + cos α sin β sin ( α − β ) = sin α cos β − cos α sin β cos ( α + β ) = cos α cos β − sin α sin β cos ( α − β ) = cos α cos β + sin α sin β {\displaystyle {\begin{aligned}\sin(\alpha +\beta )&=\sin \alpha \cos \beta +\cos \alpha \sin \beta \\\sin(\alpha -\beta )&=\sin \alpha \cos \beta -\cos \alpha \sin \beta \\\cos(\alpha +\beta )&=\cos \alpha \cos \beta -\sin \alpha \sin \beta \\\cos(\alpha -\beta )&=\cos \alpha \cos \beta +\sin \alpha \sin \beta \end{aligned}}}
The angle difference identities for sin ( α − β ) {\displaystyle \sin(\alpha -\beta )} cos ( α − β ) {\displaystyle \cos(\alpha -\beta )} − β {\displaystyle -\beta } β {\displaystyle \beta } sin ( − β ) = − sin ( β ) {\displaystyle \sin(-\beta )=-\sin(\beta )} cos ( − β ) = cos ( β ) {\displaystyle \cos(-\beta )=\cos(\beta )}
These identities are summarized in the first two rows of the following table, which also includes sum and difference identities for the other trigonometric functions.
Sine sin ( α ± β ) {\displaystyle \sin(\alpha \pm \beta )} = {\displaystyle =} sin α cos β ± cos α sin β {\displaystyle \sin \alpha \cos \beta \pm \cos \alpha \sin \beta } [ 5] [ 6] Cosine cos ( α ± β ) {\displaystyle \cos(\alpha \pm \beta )} = {\displaystyle =} cos α cos β ∓ sin α sin β {\displaystyle \cos \alpha \cos \beta \mp \sin \alpha \sin \beta } [ 6] [ 7] Tangent tan ( α ± β ) {\displaystyle \tan(\alpha \pm \beta )} = {\displaystyle =} tan α ± tan β 1 ∓ tan α tan β {\displaystyle {\frac {\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }}} [ 6] [ 8] Cosecant csc ( α ± β ) {\displaystyle \csc(\alpha \pm \beta )} = {\displaystyle =} sec α sec β csc α csc β sec α csc β ± csc α sec β {\displaystyle {\frac {\sec \alpha \sec \beta \csc \alpha \csc \beta }{\sec \alpha \csc \beta \pm \csc \alpha \sec \beta }}} [ 9] Secant sec ( α ± β ) {\displaystyle \sec(\alpha \pm \beta )} = {\displaystyle =} sec α sec β csc α csc β csc α csc β ∓ sec α sec β {\displaystyle {\frac {\sec \alpha \sec \beta \csc \alpha \csc \beta }{\csc \alpha \csc \beta \mp \sec \alpha \sec \beta }}} [ 9] Cotangent cot ( α ± β ) {\displaystyle \cot(\alpha \pm \beta )} = {\displaystyle =} cot α cot β ∓ 1 cot β ± cot α {\displaystyle {\frac {\cot \alpha \cot \beta \mp 1}{\cot \beta \pm \cot \alpha }}} [ 6] [ 10] Arcsine arcsin x ± arcsin y {\displaystyle \arcsin x\pm \arcsin y} = {\displaystyle =} arcsin ( x 1 − y 2 ± y 1 − x 2 y ) {\displaystyle \arcsin \left(x{\sqrt {1-y^{2}}}\pm y{\sqrt {1-x^{2}{\vphantom {y}}}}\right)} [ 11] Arccosine arccos x ± arccos y {\displaystyle \arccos x\pm \arccos y} = {\displaystyle =} arccos ( x y ∓ ( 1 − x 2 ) ( 1 − y 2 ) ) {\displaystyle \arccos \left(xy\mp {\sqrt {\left(1-x^{2}\right)\left(1-y^{2}\right)}}\right)} [ 12] Arctangent arctan x ± arctan y {\displaystyle \arctan x\pm \arctan y} = {\displaystyle =} arctan ( x ± y 1 ∓ x y ) {\displaystyle \arctan \left({\frac {x\pm y}{1\mp xy}}\right)} [ 13] Arccotangent arccot x ± arccot y {\displaystyle \operatorname {arccot} x\pm \operatorname {arccot} y} = {\displaystyle =} arccot ( x y ∓ 1 y ± x ) {\displaystyle \operatorname {arccot} \left({\frac {xy\mp 1}{y\pm x}}\right)}
Sines and cosines of sums of infinitely many angles [ edit ] When the series ∑ i = 1 ∞ θ i {\textstyle \sum _{i=1}^{\infty }\theta _{i}} converges absolutely then
sin ( ∑ i = 1 ∞ θ i ) = ∑ odd k ≥ 1 ( − 1 ) k − 1 2 ∑ A ⊆ { 1 , 2 , 3 , … } | A | = k ( ∏ i ∈ A sin θ i ∏ i ∉ A cos θ i ) cos ( ∑ i = 1 ∞ θ i ) = ∑ even k ≥ 0 ( − 1 ) k 2 ∑ A ⊆ { 1 , 2 , 3 , … } | A | = k ( ∏ i ∈ A sin θ i ∏ i ∉ A cos θ i ) . {\displaystyle {\begin{aligned}{\sin }{\biggl (}\sum _{i=1}^{\infty }\theta _{i}{\biggl )}&=\sum _{{\text{odd}}\ k\geq 1}(-1)^{\frac {k-1}{2}}\!\!\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}{\biggl (}\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}{\biggr )}\\{\cos }{\biggl (}\sum _{i=1}^{\infty }\theta _{i}{\biggr )}&=\sum _{{\text{even}}\ k\geq 0}(-1)^{\frac {k}{2}}\,\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}{\biggl (}\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}{\biggr )}.\end{aligned}}}
Because the series ∑ i = 1 ∞ θ i {\textstyle \sum _{i=1}^{\infty }\theta _{i}} lim i → ∞ θ i = 0 , {\textstyle \lim _{i\to \infty }\theta _{i}=0,} lim i → ∞ sin θ i = 0 , {\textstyle \lim _{i\to \infty }\sin \theta _{i}=0,} lim i → ∞ cos θ i = 1. {\textstyle \lim _{i\to \infty }\cos \theta _{i}=1.} cofinitely many cosine factors. Terms with infinitely many sine factors would necessarily be equal to zero.
When only finitely many of the angles θ i {\displaystyle \theta _{i}}
Tangents and cotangents of sums [ edit ] Let e k {\displaystyle e_{k}} k = 0 , 1 , 2 , 3 , … {\displaystyle k=0,1,2,3,\ldots } k th-degree elementary symmetric polynomial in the variables x i = tan θ i {\displaystyle x_{i}=\tan \theta _{i}} i = 0 , 1 , 2 , 3 , … , {\displaystyle i=0,1,2,3,\ldots ,}
e 0 = 1 e 1 = ∑ i x i = ∑ i tan θ i e 2 = ∑ i < j x i x j = ∑ i < j tan θ i tan θ j e 3 = ∑ i < j < k x i x j x k = ∑ i < j < k tan θ i tan θ j tan θ k ⋮ ⋮ {\displaystyle {\begin{aligned}e_{0}&=1\\[6pt]e_{1}&=\sum _{i}x_{i}&&=\sum _{i}\tan \theta _{i}\\[6pt]e_{2}&=\sum _{i<j}x_{i}x_{j}&&=\sum _{i<j}\tan \theta _{i}\tan \theta _{j}\\[6pt]e_{3}&=\sum _{i<j<k}x_{i}x_{j}x_{k}&&=\sum _{i<j<k}\tan \theta _{i}\tan \theta _{j}\tan \theta _{k}\\&\ \ \vdots &&\ \ \vdots \end{aligned}}}
Then
tan ( ∑ i θ i ) = sin ( ∑ i θ i ) / ∏ i cos θ i cos ( ∑ i θ i ) / ∏ i cos θ i = ∑ odd k ≥ 1 ( − 1 ) k − 1 2 ∑ A ⊆ { 1 , 2 , 3 , … } | A | = k ∏ i ∈ A tan θ i ∑ even k ≥ 0 ( − 1 ) k 2 ∑ A ⊆ { 1 , 2 , 3 , … } | A | = k ∏ i ∈ A tan θ i = e 1 − e 3 + e 5 − ⋯ e 0 − e 2 + e 4 − ⋯ cot ( ∑ i θ i ) = e 0 − e 2 + e 4 − ⋯ e 1 − e 3 + e 5 − ⋯ {\displaystyle {\begin{aligned}{\tan }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {{\sin }{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}{{\cos }{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}}\\[10pt]&={\frac {\displaystyle \sum _{{\text{odd}}\ k\geq 1}(-1)^{\frac {k-1}{2}}\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}{\displaystyle \sum _{{\text{even}}\ k\geq 0}~(-1)^{\frac {k}{2}}~~\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}}={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }}\\[10pt]{\cot }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {e_{0}-e_{2}+e_{4}-\cdots }{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}
using the sine and cosine sum formulae above.
The number of terms on the right side depends on the number of terms on the left side.
For example: tan ( θ 1 + θ 2 ) = e 1 e 0 − e 2 = x 1 + x 2 1 − x 1 x 2 = tan θ 1 + tan θ 2 1 − tan θ 1 tan θ 2 , tan ( θ 1 + θ 2 + θ 3 ) = e 1 − e 3 e 0 − e 2 = ( x 1 + x 2 + x 3 ) − ( x 1 x 2 x 3 ) 1 − ( x 1 x 2 + x 1 x 3 + x 2 x 3 ) , tan ( θ 1 + θ 2 + θ 3 + θ 4 ) = e 1 − e 3 e 0 − e 2 + e 4 = ( x 1 + x 2 + x 3 + x 4 ) − ( x 1 x 2 x 3 + x 1 x 2 x 4 + x 1 x 3 x 4 + x 2 x 3 x 4 ) 1 − ( x 1 x 2 + x 1 x 3 + x 1 x 4 + x 2 x 3 + x 2 x 4 + x 3 x 4 ) + ( x 1 x 2 x 3 x 4 ) , {\displaystyle {\begin{aligned}\tan(\theta _{1}+\theta _{2})&={\frac {e_{1}}{e_{0}-e_{2}}}={\frac {x_{1}+x_{2}}{1\ -\ x_{1}x_{2}}}={\frac {\tan \theta _{1}+\tan \theta _{2}}{1\ -\ \tan \theta _{1}\tan \theta _{2}}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\[8pt]&={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}}
and so on. The case of only finitely many terms can be proved by mathematical induction .[ 14] [ 15]
Secants and cosecants of sums [ edit ] sec ( ∑ i θ i ) = ∏ i sec θ i e 0 − e 2 + e 4 − ⋯ csc ( ∑ i θ i ) = ∏ i sec θ i e 1 − e 3 + e 5 − ⋯ {\displaystyle {\begin{aligned}{\sec }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {\prod _{i}\sec \theta _{i}}{e_{0}-e_{2}+e_{4}-\cdots }}\\[8pt]{\csc }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {\prod _{i}\sec \theta _{i}}{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}
where e k {\displaystyle e_{k}} k th-degree elementary symmetric polynomial in the n variables x i = tan θ i , {\displaystyle x_{i}=\tan \theta _{i},} i = 1 , … , n , {\displaystyle i=1,\ldots ,n,} [ 16]
For example,
sec ( α + β + γ ) = sec α sec β sec γ 1 − tan α tan β − tan α tan γ − tan β tan γ csc ( α + β + γ ) = sec α sec β sec γ tan α + tan β + tan γ − tan α tan β tan γ . {\displaystyle {\begin{aligned}\sec(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{1-\tan \alpha \tan \beta -\tan \alpha \tan \gamma -\tan \beta \tan \gamma }}\\[8pt]\csc(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{\tan \alpha +\tan \beta +\tan \gamma -\tan \alpha \tan \beta \tan \gamma }}.\end{aligned}}}
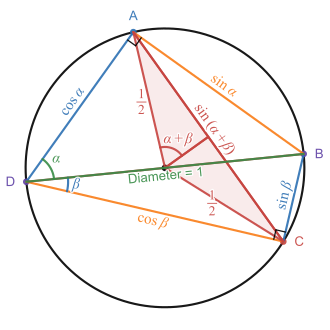
Diagram illustrating the relation between Ptolemy's theorem and the angle sum trig identity for sine. Ptolemy's theorem states that the sum of the products of the lengths of opposite sides is equal to the product of the lengths of the diagonals. When those side-lengths are expressed in terms of the sin and cos values shown in the figure above, this yields the angle sum trigonometric identity for sine: sin(α + β ) = sin α cos β + cos α sin β . Ptolemy's theorem is important in the history of trigonometric identities, as it is how results equivalent to the sum and difference formulas for sine and cosine were first proved. It states that in a cyclic quadrilateral A B C D {\displaystyle ABCD} [ 17]
By Thales's theorem , ∠ D A B {\displaystyle \angle DAB} ∠ D C B {\displaystyle \angle DCB} D A B {\displaystyle DAB} D C B {\displaystyle DCB} B D ¯ {\displaystyle {\overline {BD}}} A B ¯ = sin α {\displaystyle {\overline {AB}}=\sin \alpha } A D ¯ = cos α {\displaystyle {\overline {AD}}=\cos \alpha } B C ¯ = sin β {\displaystyle {\overline {BC}}=\sin \beta } C D ¯ = cos β {\displaystyle {\overline {CD}}=\cos \beta }
By the inscribed angle theorem, the central angle subtended by the chord A C ¯ {\displaystyle {\overline {AC}}} ∠ A D C {\displaystyle \angle ADC} 2 ( α + β ) {\displaystyle 2(\alpha +\beta )} α + β {\displaystyle \alpha +\beta } 1 2 {\textstyle {\frac {1}{2}}} A C ¯ {\displaystyle {\overline {AC}}} 2 × 1 2 sin ( α + β ) {\textstyle 2\times {\frac {1}{2}}\sin(\alpha +\beta )} sin ( α + β ) {\displaystyle \sin(\alpha +\beta )} sin ( α + β ) {\displaystyle \sin(\alpha +\beta )}
When these values are substituted into the statement of Ptolemy's theorem that | A C ¯ | ⋅ | B D ¯ | = | A B ¯ | ⋅ | C D ¯ | + | A D ¯ | ⋅ | B C ¯ | {\displaystyle |{\overline {AC}}|\cdot |{\overline {BD}}|=|{\overline {AB}}|\cdot |{\overline {CD}}|+|{\overline {AD}}|\cdot |{\overline {BC}}|} sin ( α + β ) = sin α cos β + cos α sin β {\displaystyle \sin(\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta } sin ( α − β ) {\displaystyle \sin(\alpha -\beta )} C D ¯ {\displaystyle {\overline {CD}}} B D ¯ {\displaystyle {\overline {BD}}} [ 17]
Tn is the n th Chebyshev polynomial cos ( n θ ) = T n ( cos θ ) {\displaystyle \cos(n\theta )=T_{n}(\cos \theta )} [ 18] de Moivre's formula , i is the imaginary unit cos ( n θ ) + i sin ( n θ ) = ( cos θ + i sin θ ) n {\displaystyle \cos(n\theta )+i\sin(n\theta )=(\cos \theta +i\sin \theta )^{n}} [ 19]
Visual demonstration of the double-angle formula for sine. For the above isosceles triangle with unit sides and angle 2 θ {\displaystyle 2\theta } 1 / 2 × base × height is calculated in two orientations. When upright, the area is sin θ cos θ {\displaystyle \sin \theta \cos \theta } 1 2 sin 2 θ {\textstyle {\frac {1}{2}}\sin 2\theta } sin 2 θ = 2 sin θ cos θ . {\displaystyle \sin 2\theta =2\sin \theta \cos \theta .} Formulae for twice an angle.[ 20]
sin ( 2 θ ) = 2 sin θ cos θ = ( sin θ + cos θ ) 2 − 1 = 2 tan θ 1 + tan 2 θ {\displaystyle \sin(2\theta )=2\sin \theta \cos \theta =(\sin \theta +\cos \theta )^{2}-1={\frac {2\tan \theta }{1+\tan ^{2}\theta }}} cos ( 2 θ ) = cos 2 θ − sin 2 θ = 2 cos 2 θ − 1 = 1 − 2 sin 2 θ = 1 − tan 2 θ 1 + tan 2 θ {\displaystyle \cos(2\theta )=\cos ^{2}\theta -\sin ^{2}\theta =2\cos ^{2}\theta -1=1-2\sin ^{2}\theta ={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}} tan ( 2 θ ) = 2 tan θ 1 − tan 2 θ {\displaystyle \tan(2\theta )={\frac {2\tan \theta }{1-\tan ^{2}\theta }}} cot ( 2 θ ) = cot 2 θ − 1 2 cot θ = 1 − tan 2 θ 2 tan θ {\displaystyle \cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot \theta }}={\frac {1-\tan ^{2}\theta }{2\tan \theta }}} sec ( 2 θ ) = sec 2 θ 2 − sec 2 θ = 1 + tan 2 θ 1 − tan 2 θ {\displaystyle \sec(2\theta )={\frac {\sec ^{2}\theta }{2-\sec ^{2}\theta }}={\frac {1+\tan ^{2}\theta }{1-\tan ^{2}\theta }}} csc ( 2 θ ) = sec θ csc θ 2 = 1 + tan 2 θ 2 tan θ {\displaystyle \csc(2\theta )={\frac {\sec \theta \csc \theta }{2}}={\frac {1+\tan ^{2}\theta }{2\tan \theta }}} Formulae for triple angles.[ 20]
sin ( 3 θ ) = 3 sin θ − 4 sin 3 θ = 4 sin θ sin ( π 3 − θ ) sin ( π 3 + θ ) {\displaystyle \sin(3\theta )=3\sin \theta -4\sin ^{3}\theta =4\sin \theta \sin \left({\frac {\pi }{3}}-\theta \right)\sin \left({\frac {\pi }{3}}+\theta \right)} cos ( 3 θ ) = 4 cos 3 θ − 3 cos θ = 4 cos θ cos ( π 3 − θ ) cos ( π 3 + θ ) {\displaystyle \cos(3\theta )=4\cos ^{3}\theta -3\cos \theta =4\cos \theta \cos \left({\frac {\pi }{3}}-\theta \right)\cos \left({\frac {\pi }{3}}+\theta \right)} tan ( 3 θ ) = 3 tan θ − tan 3 θ 1 − 3 tan 2 θ = tan θ tan ( π 3 − θ ) tan ( π 3 + θ ) {\displaystyle \tan(3\theta )={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}=\tan \theta \tan \left({\frac {\pi }{3}}-\theta \right)\tan \left({\frac {\pi }{3}}+\theta \right)} cot ( 3 θ ) = 3 cot θ − cot 3 θ 1 − 3 cot 2 θ {\displaystyle \cot(3\theta )={\frac {3\cot \theta -\cot ^{3}\theta }{1-3\cot ^{2}\theta }}} sec ( 3 θ ) = sec 3 θ 4 − 3 sec 2 θ {\displaystyle \sec(3\theta )={\frac {\sec ^{3}\theta }{4-3\sec ^{2}\theta }}} csc ( 3 θ ) = csc 3 θ 3 csc 2 θ − 4 {\displaystyle \csc(3\theta )={\frac {\csc ^{3}\theta }{3\csc ^{2}\theta -4}}} Formulae for multiple angles.[ 21]
sin ( n θ ) = ∑ k odd ( − 1 ) k − 1 2 ( n k ) cos n − k θ sin k θ = sin θ ∑ i = 0 ( n + 1 ) / 2 ∑ j = 0 i ( − 1 ) i − j ( n 2 i + 1 ) ( i j ) cos n − 2 ( i − j ) − 1 θ = 2 ( n − 1 ) ∏ k = 0 n − 1 sin ( k π / n + θ ) {\displaystyle {\begin{aligned}\sin(n\theta )&=\sum _{k{\text{ odd}}}(-1)^{\frac {k-1}{2}}{n \choose k}\cos ^{n-k}\theta \sin ^{k}\theta =\sin \theta \sum _{i=0}^{(n+1)/2}\sum _{j=0}^{i}(-1)^{i-j}{n \choose 2i+1}{i \choose j}\cos ^{n-2(i-j)-1}\theta \\{}&=2^{(n-1)}\prod _{k=0}^{n-1}\sin(k\pi /n+\theta )\end{aligned}}} cos ( n θ ) = ∑ k even ( − 1 ) k 2 ( n k ) cos n − k θ sin k θ = ∑ i = 0 n / 2 ∑ j = 0 i ( − 1 ) i − j ( n 2 i ) ( i j ) cos n − 2 ( i − j ) θ {\displaystyle \cos(n\theta )=\sum _{k{\text{ even}}}(-1)^{\frac {k}{2}}{n \choose k}\cos ^{n-k}\theta \sin ^{k}\theta =\sum _{i=0}^{n/2}\sum _{j=0}^{i}(-1)^{i-j}{n \choose 2i}{i \choose j}\cos ^{n-2(i-j)}\theta } cos ( ( 2 n + 1 ) θ ) = ( − 1 ) n 2 2 n ∏ k = 0 2 n cos ( k π / ( 2 n + 1 ) − θ ) {\displaystyle \cos((2n+1)\theta )=(-1)^{n}2^{2n}\prod _{k=0}^{2n}\cos(k\pi /(2n+1)-\theta )} cos ( 2 n θ ) = ( − 1 ) n 2 2 n − 1 ∏ k = 0 2 n − 1 cos ( ( 1 + 2 k ) π / ( 4 n ) − θ ) {\displaystyle \cos(2n\theta )=(-1)^{n}2^{2n-1}\prod _{k=0}^{2n-1}\cos((1+2k)\pi /(4n)-\theta )} tan ( n θ ) = ∑ k odd ( − 1 ) k − 1 2 ( n k ) tan k θ ∑ k even ( − 1 ) k 2 ( n k ) tan k θ {\displaystyle \tan(n\theta )={\frac {\sum _{k{\text{ odd}}}(-1)^{\frac {k-1}{2}}{n \choose k}\tan ^{k}\theta }{\sum _{k{\text{ even}}}(-1)^{\frac {k}{2}}{n \choose k}\tan ^{k}\theta }}} The Chebyshev method is a recursive algorithm for finding the n th multiple angle formula knowing the ( n − 1 ) {\displaystyle (n-1)} ( n − 2 ) {\displaystyle (n-2)} [ 22]
cos ( n x ) {\displaystyle \cos(nx)} cos ( ( n − 1 ) x ) {\displaystyle \cos((n-1)x)} cos ( ( n − 2 ) x ) {\displaystyle \cos((n-2)x)} cos ( x ) {\displaystyle \cos(x)}
cos ( n x ) = 2 cos x cos ( ( n − 1 ) x ) − cos ( ( n − 2 ) x ) . {\displaystyle \cos(nx)=2\cos x\cos((n-1)x)-\cos((n-2)x).}
This can be proved by adding together the formulae
cos ( ( n − 1 ) x + x ) = cos ( ( n − 1 ) x ) cos x − sin ( ( n − 1 ) x ) sin x cos ( ( n − 1 ) x − x ) = cos ( ( n − 1 ) x ) cos x + sin ( ( n − 1 ) x ) sin x {\displaystyle {\begin{aligned}\cos((n-1)x+x)&=\cos((n-1)x)\cos x-\sin((n-1)x)\sin x\\\cos((n-1)x-x)&=\cos((n-1)x)\cos x+\sin((n-1)x)\sin x\end{aligned}}}
It follows by induction that cos ( n x ) {\displaystyle \cos(nx)} cos x , {\displaystyle \cos x,} Chebyshev polynomials#Trigonometric definition .
Similarly, sin ( n x ) {\displaystyle \sin(nx)} sin ( ( n − 1 ) x ) , {\displaystyle \sin((n-1)x),} sin ( ( n − 2 ) x ) , {\displaystyle \sin((n-2)x),} cos x {\displaystyle \cos x} sin ( n x ) = 2 cos x sin ( ( n − 1 ) x ) − sin ( ( n − 2 ) x ) {\displaystyle \sin(nx)=2\cos x\sin((n-1)x)-\sin((n-2)x)} sin ( ( n − 1 ) x + x ) {\displaystyle \sin((n-1)x+x)} sin ( ( n − 1 ) x − x ) . {\displaystyle \sin((n-1)x-x).}
Serving a purpose similar to that of the Chebyshev method, for the tangent we can write:
tan ( n x ) = tan ( ( n − 1 ) x ) + tan x 1 − tan ( ( n − 1 ) x ) tan x . {\displaystyle \tan(nx)={\frac {\tan((n-1)x)+\tan x}{1-\tan((n-1)x)\tan x}}\,.}
sin θ 2 = sgn ( sin θ 2 ) 1 − cos θ 2 cos θ 2 = sgn ( cos θ 2 ) 1 + cos θ 2 tan θ 2 = 1 − cos θ sin θ = sin θ 1 + cos θ = csc θ − cot θ = tan θ 1 + sec θ = sgn ( sin θ ) 1 − cos θ 1 + cos θ = − 1 + sgn ( cos θ ) 1 + tan 2 θ tan θ cot θ 2 = 1 + cos θ sin θ = sin θ 1 − cos θ = csc θ + cot θ = sgn ( sin θ ) 1 + cos θ 1 − cos θ sec θ 2 = sgn ( cos θ 2 ) 2 1 + cos θ csc θ 2 = sgn ( sin θ 2 ) 2 1 − cos θ {\displaystyle {\begin{aligned}\sin {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {1-\cos \theta }{2}}}\\[3pt]\cos {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {1+\cos \theta }{2}}}\\[3pt]\tan {\frac {\theta }{2}}&={\frac {1-\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1+\cos \theta }}=\csc \theta -\cot \theta ={\frac {\tan \theta }{1+\sec {\theta }}}\\[6mu]&=\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}={\frac {-1+\operatorname {sgn}(\cos \theta ){\sqrt {1+\tan ^{2}\theta }}}{\tan \theta }}\\[3pt]\cot {\frac {\theta }{2}}&={\frac {1+\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1-\cos \theta }}=\csc \theta +\cot \theta =\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\\sec {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1+\cos \theta }}}\\\csc {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1-\cos \theta }}}\\\end{aligned}}} [ 23] [ 24]
Also tan η ± θ 2 = sin η ± sin θ cos η + cos θ































































































































![{\displaystyle {\begin{aligned}\operatorname {sgn}(\sin \theta )=\operatorname {sgn}(\csc \theta )&={\begin{cases}+1&{\text{if}}\ \ 0<\theta <\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <0\\0&{\text{if}}\ \ \theta \in \{0,\pi \}\end{cases}}\\[5mu]\operatorname {sgn}(\cos \theta )=\operatorname {sgn}(\sec \theta )&={\begin{cases}+1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },{\tfrac {1}{2}}\pi {\bigr \}}\end{cases}}\\[5mu]\operatorname {sgn}(\tan \theta )=\operatorname {sgn}(\cot \theta )&={\begin{cases}+1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ 0<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <0\ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },0,{\tfrac {1}{2}}\pi ,\pi {\bigr \}}\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14cc79239a0fcdfb53b132d75a93474e9e6d5ba0)

![{\displaystyle ({-\pi },\pi ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/122328145a5f3a4162d21b4fbb5f4d1149932d2b)






































![{\displaystyle {\begin{aligned}e_{0}&=1\\[6pt]e_{1}&=\sum _{i}x_{i}&&=\sum _{i}\tan \theta _{i}\\[6pt]e_{2}&=\sum _{i<j}x_{i}x_{j}&&=\sum _{i<j}\tan \theta _{i}\tan \theta _{j}\\[6pt]e_{3}&=\sum _{i<j<k}x_{i}x_{j}x_{k}&&=\sum _{i<j<k}\tan \theta _{i}\tan \theta _{j}\tan \theta _{k}\\&\ \ \vdots &&\ \ \vdots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb1927ae2be96f5156e18813a20486fdb0ff72f1)
![{\displaystyle {\begin{aligned}{\tan }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {{\sin }{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}{{\cos }{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}}\\[10pt]&={\frac {\displaystyle \sum _{{\text{odd}}\ k\geq 1}(-1)^{\frac {k-1}{2}}\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}{\displaystyle \sum _{{\text{even}}\ k\geq 0}~(-1)^{\frac {k}{2}}~~\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}}={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }}\\[10pt]{\cot }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {e_{0}-e_{2}+e_{4}-\cdots }{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d02567417a5a013481366384787e518cd74c68be)
![{\displaystyle {\begin{aligned}\tan(\theta _{1}+\theta _{2})&={\frac {e_{1}}{e_{0}-e_{2}}}={\frac {x_{1}+x_{2}}{1\ -\ x_{1}x_{2}}}={\frac {\tan \theta _{1}+\tan \theta _{2}}{1\ -\ \tan \theta _{1}\tan \theta _{2}}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\[8pt]&={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c9196b8ab5e0aef6cf7d7fec7d7546f2a6e7d2f)
![{\displaystyle {\begin{aligned}{\sec }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {\prod _{i}\sec \theta _{i}}{e_{0}-e_{2}+e_{4}-\cdots }}\\[8pt]{\csc }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {\prod _{i}\sec \theta _{i}}{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b24f2b169fbe11608507c63f5bb728e03b2b4957)


![{\displaystyle {\begin{aligned}\sec(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{1-\tan \alpha \tan \beta -\tan \alpha \tan \gamma -\tan \beta \tan \gamma }}\\[8pt]\csc(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{\tan \alpha +\tan \beta +\tan \gamma -\tan \alpha \tan \beta \tan \gamma }}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e082e69aab7a9c782f590f3a93262ba3101899b7)




























































![{\displaystyle {\begin{aligned}\sin {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {1-\cos \theta }{2}}}\\[3pt]\cos {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {1+\cos \theta }{2}}}\\[3pt]\tan {\frac {\theta }{2}}&={\frac {1-\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1+\cos \theta }}=\csc \theta -\cot \theta ={\frac {\tan \theta }{1+\sec {\theta }}}\\[6mu]&=\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}={\frac {-1+\operatorname {sgn}(\cos \theta ){\sqrt {1+\tan ^{2}\theta }}}{\tan \theta }}\\[3pt]\cot {\frac {\theta }{2}}&={\frac {1+\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1-\cos \theta }}=\csc \theta +\cot \theta =\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\\sec {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1+\cos \theta }}}\\\csc {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1-\cos \theta }}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d53d104c73c4b28f1dd7bfa5d2b0c7207c68cd87)