圖乘積

此條目没有列出任何参考或来源。 (2020年3月23日) |
在圖論中,圖乘積為一個在圖上的二元運算,精確地說,這是一個需要兩個圖G1和G2,並產生出圖H 有著以下性質
- 圖H的頂點集合 是 笛卡爾乘積 V(G1) × V(G2),其中 V(G1)和 V(G2)分別是圖 G1 和 G2的頂點集合。
- H的兩個頂點(u1, u2)和(v1, v2) 是由一條邊所連接頂點 u1, u2, v1, v2滿足一個條件需要將圖 G1 和 G2的邊列入考慮。
關於用詞以及符號對於特定的圖乘積有非常多,讀者應當注意去確認作者使用的定義
圖表
[编辑]以下的表格顯示了常見的圖乘積,並用記作兩頂點有被一條邊連接,用記作兩頂點有未被一條邊連接
| 各種乘積 | 當的情況 | 頂點數與邊數
| 範例 |
|---|---|---|---|
| 笛卡爾乘積(圖論)
| ( = and ) 或是 ( and = ) | 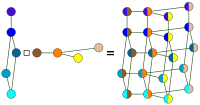 | |
| 張量積(圖論)
| and |  | |
| 強乘積(AND乘積)
| ( u1 = v1 and u2 ∼ v2 ) 或是 ( u1 ∼ v1 and u2 = v2 ) 或是 ( u1 ∼ v1 and u2 ∼ v2 ) | ||
| 弱乘積(OR乘積)
| 或是
| ||
| 根乘積 |  |
其他概念
[编辑]參考
[编辑]

















