调和矩阵

此條目翻譯品質不佳。 (2020年2月17日) 翻譯者可能不熟悉中文或原文語言，也可能使用了機器翻譯。請協助翻譯本條目或重新編寫，并注意避免翻译腔的问题。明顯拙劣的翻譯請改掛{{d|G13}}提交刪除。

在图论中，调和矩阵（harmonic matrix），也称拉普拉斯矩阵或拉氏矩阵（Laplacian matrix）、离散拉普拉斯（discrete Laplacian），是图的矩阵表示。^[1]

调和矩阵也是拉普拉斯算子的离散化。换句话说，调和矩阵的缩放极限是拉普拉斯算子。它在机器学习和物理学中有很多应用。

若G是简单图，G有n个顶点，A是邻接矩阵，D是度数矩阵，则调和矩阵是^[1]

${\displaystyle L=D-A}$

${\displaystyle L_{i,j}:={\begin{cases}\deg(v_{i})&{\mbox{if}}\ i=j\\-1&{\mbox{if}}\ i\neq j\ {\mbox{and}}\ v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}\end{cases}}}$

这跟拉普拉斯算子有什么关系？若f 是加权图G的顶点函数，则^[2]

${\displaystyle E(f)=\sum w(uv)(f(u)-f(v))^{2}/2=f^{t}Lf}$

w是边的权重函数。u、v是顶点。f = (f(1), ..., f(n)) 是n维的矢量。上面泛函也称为Dirichlet泛函。^[3]

而且若K是接续矩阵（incidence matrix），则^[2]

${\displaystyle K_{ev}=\left\{{\begin{array}{rl}1,&{\text{if }}v=i\\-1,&{\text{if }}v=j\\0,&{\text{otherwise}}.\end{array}}\right.}$

${\displaystyle L=K^{t}K}$

Kf 是f 的图梯度。另外，特征值满足

${\displaystyle {\begin{aligned}\lambda _{i}&=\mathbf {v} _{i}^{\textsf {T}}L\mathbf {v} _{i}\\&=\mathbf {v} _{i}^{\textsf {T}}M^{\textsf {T}}M\mathbf {v} _{i}\\&=\left(M\mathbf {v} _{i}\right)^{\textsf {T}}\left(M\mathbf {v} _{i}\right)\\\end{aligned}}}$

图	度矩阵	邻接矩阵	调和矩阵
	${\textstyle \left({\begin{array}{rrrrrr}2&0&0&0&0&0\\0&3&0&0&0&0\\0&0&2&0&0&0\\0&0&0&3&0&0\\0&0&0&0&3&0\\0&0&0&0&0&1\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrrrr}0&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\\\end{array}}\right)}$	${\textstyle \left({\begin{array}{rrrrrr}2&-1&0&0&-1&0\\-1&3&-1&0&-1&0\\0&-1&2&-1&0&0\\0&0&-1&3&-1&-1\\-1&-1&0&-1&3&0\\0&0&0&-1&0&1\\\end{array}}\right)}$

${\displaystyle L^{\text{sym}}:=D^{-{\frac {1}{2}}}LD^{-{\frac {1}{2}}}=I-D^{-{\frac {1}{2}}}AD^{-{\frac {1}{2}}}}$

${\displaystyle L_{i,j}^{\text{sym}}:={\begin{cases}1&{\mbox{if }}i=j{\mbox{ and }}\deg(v_{i})\neq 0\\-{\frac {1}{\sqrt {\deg(v_{i})\deg(v_{j})}}}&{\mbox{if }}i\neq j{\mbox{ and }}v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}.\end{cases}}}$

注意^[4]

${\displaystyle \lambda \ =\ {\frac {\langle g,L^{\text{sym}}g\rangle }{\langle g,g\rangle }}\ =\ {\frac {\left\langle g,D^{-{\frac {1}{2}}}LD^{-{\frac {1}{2}}}g\right\rangle }{\langle g,g\rangle }}\ =\ {\frac {\langle f,Lf\rangle }{\left\langle D^{\frac {1}{2}}f,D^{\frac {1}{2}}f\right\rangle }}\ =\ {\frac {\sum _{u\sim v}(f(u)-f(v))^{2}}{\sum _{v}f(v)^{2}d_{v}}}\ \geq \ 0,}$

${\displaystyle L^{\text{rw}}:=D^{-1}L=I-D^{-1}A}$

${\displaystyle L_{i,j}^{\text{rw}}:={\begin{cases}1&{\mbox{if }}i=j{\mbox{ and }}\deg(v_{i})\neq 0\\-{\frac {1}{\deg(v_{i})}}&{\mbox{if }}i\neq j{\mbox{ and }}v_{i}{\mbox{ is adjacent to }}v_{j}\\0&{\mbox{otherwise}}.\end{cases}}}$

例如，离散的冷却定律使用调和矩阵^[5]

${\displaystyle {\begin{aligned}{\frac {d\phi _{i}}{dt}}&=-k\sum _{j}A_{ij}\left(\phi _{i}-\phi _{j}\right)\\&=-k\left(\phi _{i}\sum _{j}A_{ij}-\sum _{j}A_{ij}\phi _{j}\right)\\&=-k\left(\phi _{i}\ \deg(v_{i})-\sum _{j}A_{ij}\phi _{j}\right)\\&=-k\sum _{j}\left(\delta _{ij}\ \deg(v_{i})-A_{ij}\right)\phi _{j}\\&=-k\sum _{j}\left(\ell _{ij}\right)\phi _{j}.\end{aligned}}}$

使用矩阵矢量

${\displaystyle {\begin{aligned}{\frac {d\phi }{dt}}&=-k(D-A)\phi \\&=-kL\phi \end{aligned}}}$

${\displaystyle {\frac {d\phi }{dt}}+kL\phi =0}$

解是

${\displaystyle {\begin{aligned}{\frac {d\left(\sum _{i}c_{i}\mathbf {v} _{i}\right)}{dt}}+kL\left(\sum _{i}c_{i}\mathbf {v} _{i}\right)&=0\\\sum _{i}\left[{\frac {dc_{i}}{dt}}\mathbf {v} _{i}+kc_{i}L\mathbf {v} _{i}\right]&=\\\sum _{i}\left[{\frac {dc_{i}}{dt}}\mathbf {v} _{i}+kc_{i}\lambda _{i}\mathbf {v} _{i}\right]&=\\{\frac {dc_{i}}{dt}}+k\lambda _{i}c_{i}&=0\\\end{aligned}}}$

${\displaystyle c_{i}(t)=c_{i}(0)e^{-k\lambda _{i}t}}$

${\displaystyle c_{i}(0)=\left\langle \phi (0),\mathbf {v} _{i}\right\rangle }$

当${\textstyle \lim _{t\to \infty }\phi (t)}$的时候，

${\displaystyle \lim _{t\to \infty }e^{-k\lambda _{i}t}=\left\{{\begin{array}{rlr}0&{\text{if}}&\lambda _{i}>0\\1&{\text{if}}&\lambda _{i}=0\end{array}}\right\}}$

${\displaystyle \lim _{t\to \infty }\phi (t)=\left\langle c(0),\mathbf {v^{1}} \right\rangle \mathbf {v^{1}} }$

${\displaystyle \mathbf {v^{1}} ={\frac {1}{\sqrt {N}}}[1,1,...,1]}$

${\displaystyle \lim _{t\to \infty }\phi _{j}(t)={\frac {1}{N}}\sum _{i=1}^{N}c_{i}(0)}$

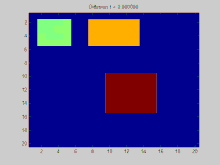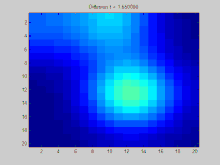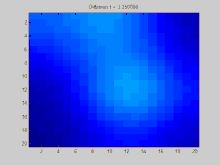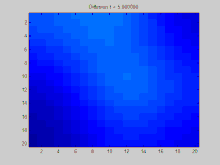
N = 20;%The number of pixels along a dimension of the image A = zeros(N, N);%The image Adj = zeros(N*N, N*N);%The adjacency matrix  %Use 8 neighbors, and fill in the adjacency matrix dx = [-1, 0, 1, -1, 1, -1, 0, 1]; dy = [-1, -1, -1, 0, 0, 1, 1, 1]; for x = 1:N    for y = 1:N        index = (x-1)*N + y;        for ne = 1:length(dx)            newx = x + dx(ne);            newy = y + dy(ne);            if newx > 0 && newx <= N && newy > 0 && newy <= N                index2 = (newx-1)*N + newy;                Adj(index, index2) = 1;            end        end    end end  %%%BELOW IS THE KEY CODE THAT COMPUTES THE SOLUTION TO THE DIFFERENTIAL %%%EQUATION Deg = diag(sum(Adj, 2));%Compute the degree matrix L = Deg - Adj;%Compute the laplacian matrix in terms of the degree and adjacency matrices [V, D] = eig(L);%Compute the eigenvalues/vectors of the laplacian matrix D = diag(D);  %Initial condition (place a few large positive values around and %make everything else zero) C0 = zeros(N, N); C0(2:5, 2:5) = 5; C0(10:15, 10:15) = 10; C0(2:5, 8:13) = 7; C0 = C0(:);  C0V = V'*C0;%Transform the initial condition into the coordinate system  %of the eigenvectors for t = 0:0.05:5    %Loop through times and decay each initial component    Phi = C0V.*exp(-D*t);%Exponential decay for each component    Phi = V*Phi;%Transform from eigenvector coordinate system to original coordinate system    Phi = reshape(Phi, N, N);    %Display the results and write to GIF file    imagesc(Phi);    caxis([0, 10]);    title(sprintf('Diffusion t = %3f', t));    frame = getframe(1);    im = frame2im(frame);    [imind, cm] = rgb2ind(im, 256);    if t == 0       imwrite(imind, cm, 'out.gif', 'gif', 'Loopcount', inf, 'DelayTime', 0.1);     else       imwrite(imind, cm, 'out.gif', 'gif', 'WriteMode', 'append', 'DelayTime', 0.1);    end end 

• Kirchoff定理：调和矩阵的行列式
• 人工智能
• 非线性降维
• 谱聚类
• Cheeger不等式：调和矩阵的第二大的特征值跟最大割問題有关
• 图Signal processing^[3]

1. ^ ^{1.0 1.1} Weisstein, Eric W. (编). Laplacian Matrix. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2020-02-14]. （原始内容存档于2019-12-23） （英语）. 
2. ^ ^{2.0 2.1} Muni Sreenivas Pydi (ముని శ్రీనివాస్ పైడి)'s answer to What's the intuition behind a Laplacian matrix? I'm not so much interested in mathematical details or technical applications. I'm trying to grasp what a laplacian matrix actually represents, and what aspects of a graph it makes accessible. - Quora. www.quora.com. [2020-02-14]. 
3. ^ ^{3.0 3.1} Shuman, David I.; Narang, Sunil K.; Frossard, Pascal; Ortega, Antonio; Vandergheynst, Pierre. The Emerging Field of Signal Processing on Graphs: Extending High-Dimensional Data Analysis to Networks and Other Irregular Domains. IEEE Signal Processing Magazine. 2013-05, 30 (3): 83–98 [2020-02-14]. ISSN 1053-5888. doi:10.1109/MSP.2012.2235192. （原始内容存档于2020-01-11）. 
4. ^ Chung, Fan. Spectral Graph Theory. American Mathematical Society. 1997 [1992] [2020-02-14]. ISBN 978-0821803158. （原始内容存档于2020-02-14）. 
5. ^ Newman, Mark. Networks: An Introduction. Oxford University Press. 2010. ISBN 978-0199206650. 

• T. Sunada. Chapter 1. Analysis on combinatorial graphs. Discrete geometric analysis. P. Exner, J. P. Keating, P. Kuchment, T. Sunada, A. Teplyaev (编). 'Proceedings of Symposia in Pure Mathematics 77. 2008: 51–86. ISBN 978-0-8218-4471-7. 
• B. Bollobás, Modern Graph Theory, Springer-Verlag (1998, corrected ed. 2013), ISBN 0-387-98488-7, Chapters II.3 (Vector Spaces and Matrices Associated with Graphs), VIII.2 (The Adjacency Matrix and the Laplacian), IX.2 (Electrical Networks and Random Walks).