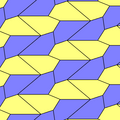
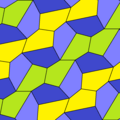
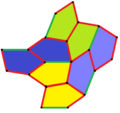
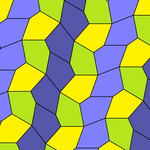
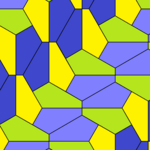
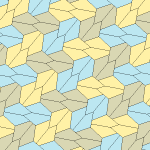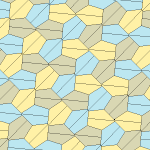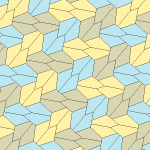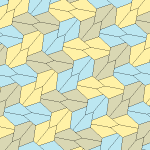
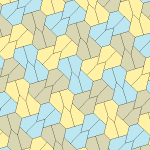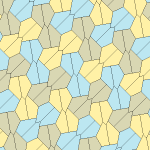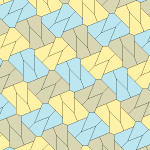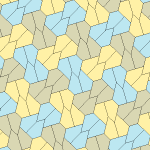
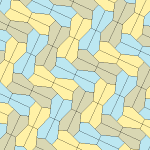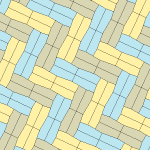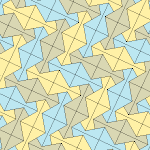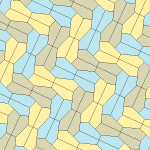
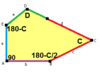
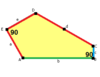
Пятиугольный паркет


Пятиугольный паркет — в геометрии: замощение, составленное из выпуклых пятиугольников. Замощение из правильных пятиугольников в евклидовом пространстве невозможно, поскольку общий угол правильного пятиугольника равен 108° и не делит ни 180°, ни 360°. Однако ими можно замостить[англ.] гиперболическую плоскость и сферу.
Для плоскости же задача о полном описании всех возможных замощений неправильными пятиугольниками (описания всех видов пятиугольников, для которых возможно такое замощение) является очень сложной и исследования по ней ведутся больше века.
Замощение плоскости одной выпуклой плиткой
[править | править код]Количество паркетов из одной выпуклой плитки
[править | править код]Пятиугольные паркеты вообще
[править | править код]Предполагается, что существует всего 15 классов пятиугольников, бесконечные паркеты из которых могут замостить плоскость. Поиск всех таких классов продолжался до 2015 года, а 1 мая 2017 года Микаэль Рао предъявил доказательство того, что других таких пятиугольников не существует[1][2]. По состоянию на декабрь 2017 года компьютерная программа, используемая и специально написанная для доказательства теоремы, независимо воспроизведена и проверена Томасом Хейлзом[вд], профессором математики Питсбургского университета[3][4], а остальная часть статьи всё ещё находится на рецензировании.
Паркеты типа «ребро к ребру»
[править | править код]Более простой задачей является отыскание всех паркетов, составляющих замощение «ребро к ребру», то есть когда ни одна сторона ни одной плитки не совпадает сразу с двумя сторонами двух других (или, другими словами, когда никакая из вершин многоугольников замощения не лежит посреди некоторой стороны другого многоугольника).
Всего существует восемь видов пятиугольных паркетных выпуклых плиток «ребро к ребру». Тот факт, что других таких видов паркетных плиток, кроме уже найденных, не существует, был доказан Ольгой Багиной на Омском алгебраическом семинаре в 2011 году[5]. Доказательство было опубликовано в 2017 году[6].
Независимо от Багиной доказательство получил также Сугимото (Sugimoto) в 2012 году[7].
Известные типы паркетов
[править | править код]Ни один из пятнадцати известных классов доступных для замощения пятиугольников не накрывается полностью объединением других. Тем не менее, некоторые пары классов могут пересекаться. Кроме того, в некоторых классах есть многоугольники, для которых кроме стандартной схемы замощения плоскости плитками этого класса существуют ещё и альтернативные способы замощения.
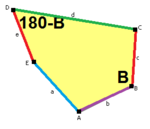
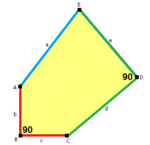
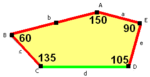
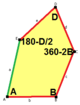
В приведенной классификации плиток углы пятиугольника обозначены через A,B,C,D,E, а длины его сторон через a, b, c, d, e, где |EA|=a, |AB|=b, |BC|=c, |CD|=d, |DE|=e. Многие из этих классов имеют степени свободы, выражающиеся уравнениями для углов и сторон. В частности, классы 1, 2, 4, 5, 6, 7, 8, 9 и 13 допускают параметры, при которых пятиугольники становятся невыпуклыми.
Периодические замощения могут быть характеризованы своей группой симметрии[англ.], например, p2 (2222) для замощений, содержащих 4 точки вращения (с учётом параллельного переноса) порядка 2 (изображение переходит в себя при повороте на 360/2=180°). Это используется далее в иллюстрациях, где одинаковыми цветами показаны, плитки мозаики, переходящие друг в друга при соответствующем повороте.
Примитивной ячейкой будем называть наименьшую из плиток, которая при копировании и переносе образует всю данную мозаику.
Типы 1,2,3,4,5 (Рейнхардт, 1918)
[править | править код]Первые пять типов замощений описал в 1918 году Карл Рейнхардт[англ.].[8] Все эти пять замощений были изоэдральными, то есть каждую из плиток можно было перевести в каждую другую обычным поворотом и переносом, без применения зеркального отражения.
Грюнбаум и Шефард показали, что существует ровно 24 типа различных изоэдральных замощений.[9] Все эти 24 типа принадлежали к классам, описанным Рейнхардтом, но иногда требовали добавочных условий. Существует по два изоэдральных замощения для каждого набора из типа 2, и по одному для каждого из четырёх остальных. 15 из 18 остальных типов представляют собой специальные случаи замощения типа 1. 9 из 24 типов относятся к паркетам «ребро к ребру».[10]
Группы симметрий рядом с картинками ниже приведены в орбифолдной нотации[англ.].
Для плиток первого типа существует множество способов замощения плоскости ими. Ниже приведены пять топологически разных примеров замощения:
| Тип 2 | |
|---|---|
| pgg (22×) | |
| p2 (2222) | |
 |  |
| Примитивная ячейка из 4 плиток | |
 c = e B + D = 180° | 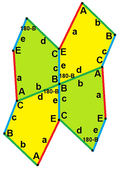 c = e, d = b B + D = 180° |
Типы 6,7,8 (Кершнер, 1968)
[править | править код]Ричард Кершнер в 1968 году описал ещё три типа плиток. Он утверждал, что, кроме найденных теперь восьми типов, других не существует, но оказался не прав.
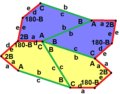
В типах 7 и 8 впервые появляются хиральные плитки (то есть для полного описания орбит симметрии впервые приходится использовать не только вращения, но и отражения). На картинке ниже пары хиральных плиток обозначены парами цветов (жёлтый, зелёный) и (синий, бледно-синий).
Все представленные ниже примеры 2-изоэдральны.
Тип 10 (Джеймс, 1975)
[править | править код]Изучив результаты Кершнера в колонке Мартина Гарднера «Математические игры» журнала Scientific American, Ричард Джеймс нашёл ещё один тип пятиугольников, который сейчас именуется типом 10.
Представленные здесь примеры 3-изоэдральны.
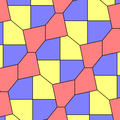
| Type 10 | |
|---|---|
| p2 (2222) | cmm (2*22) |
 |  |
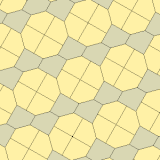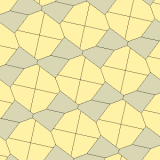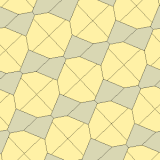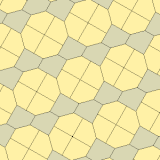 | |
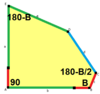 a=b=c+e A=90, B+E=180°, B+2C=360° | 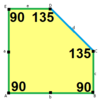 a=b=2c=2e A=B=E=90°, C=D=135° |
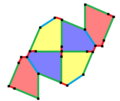 Примитивная ячейка из 6 плиток | |
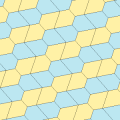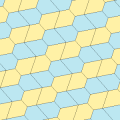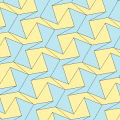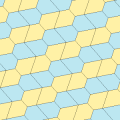
Типы 9, 11, 12, 13 (Райс, 1977)
[править | править код]Математик-любитель Марджори Райс в 1976 и 1977 году нашла ещё четыре типа плиток, подходящих для замощения.
Все четыре типа паркетов 2-изоэдральны. На картинке ниже пары хиральных плиток обозначены парами цветов (жёлтый, зелёный) и (синий, бледно-синий).
Из всех четырёх типов только тип 9 даёт замощение типа «ребро к ребру».
Примитивные ячейки везде содержат по 8 плиток.
Тип 14 (Стейн, 1985)
[править | править код]Четырнадцатую мозаику нашёл Рольф Стейн в 1985 году. Найденное им замощение 3-изоэдрально и не относится к типу «ребро к ребру».
Более того, его замощение состоит из строго фиксированных плиток — никакой вариабельности через уравнения на углы, как в предыдущих типах, никаких степеней свободы здесь нет. Вот некоторые параметры этой фиксированной плитки:
Из этих значений можно легко вывести остальные.
Примитивная ячейка такого замощения содержит шесть плиток.
| Type 14 | |||
|---|---|---|---|
| pgg (22×) | |||
 |  2a=2c=d=e A=90°, B≈145.34°, C≈69.32°, D≈124.66°, E≈110.68° (2B+C=360°, C+E=180°). |  Примитивная ячейка из 6 плиток | |
Тип 15 (Манн, Маклауд, фон Дюрей, 2015)
[править | править код]Исследователи из Вашингтонского университета в Ботелле, математики Кейси Манн, Джениффер Маклауд и Дэвид фон Дюрей в 2015 году, используя компьютерные вычисления, нашли пятнадцатый тип паркета. Их работа была опубликована в октябре 2015 года.[11]
Эта мозаика не относится к типу «ребро к ребру». Она 3-изоэдральна (это обеспечивается двумя симметриями — поворотом на 180° относительно центра стыка светло-жёлтых плиток одной элементарной ячейки и зеркальным отражением относительно центра стыка светло-жёлтых плиток из двух разных элементарных ячеек). В мозаике есть хиральные плитки — на рисунке они обозначены парами цветов (жёлтый, светло-жёлтый), (синий, голубой), (красный, розовый). Примитивная ячейка содержит 12 плиток.
Так же, как паркет типа 14, этот паркет может быть построен из одной единственной плитки, никаких степеней свободы для изменения углов и длин сторон нет.
| Type 15 | ||
|---|---|---|
 (Larger image) | 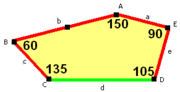 a=c=e, b=2a, d=√2 + √3a A=150°, B=60°, C=135° D=105°, E=90° | 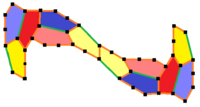 Примитивная ячейка из 12 плиток |
Непериодические паркеты
[править | править код]Непериодические паркеты из пятиугольных плиток также существуют. Они имеют радиальную симметрию, то есть совпадают с собой после поворота на некоторый угол относительно центра.
Ниже мы будем говорить о замощении с радиальной симметрией порядка если оно совпадает с собой после поворота на относительно центральной точки.
В 2016 году Бернард Клаасен показал, что для любого существует непериодическое пятиугольное замощение с радиальной симметрией порядка [12][13]. Его метод построения заключался в том, чтобы заполнять плоскость парами пятиугольников, состыкованных по одной стороне таким образом, что он образуют шестиугольник. Если один из углов пятиугольника равен и длины сторон подобраны правильным образом, то, начиная от тривиально состыкованных вокруг одной точки таких пятиугольников, можно предсказуемо заполнять окружающие их слои один за другим.
Паркеты, двойственные однородным
[править | править код]Существует три типа паркетов, двойственных однородным. Все эти паркеты относятся к типу «ребро к ребру». Симметрии в двойственных паркетах совпадают с симметриями в соответствующих однородных. Поскольку однородные паркеты изогональны, до двойственные им — изоэдральны.
| cmm (2*22) | p4g (4*2) | p6 (632) |
|---|---|---|
 | 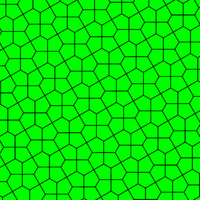 |  |
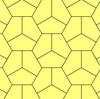
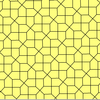
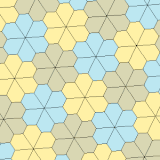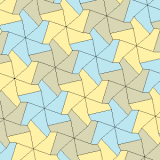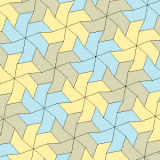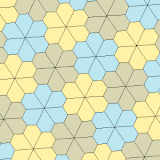
| Призматический пятиугольный паркет Экземпляр типа 1[8] | Каирская пятиугольная мозаика Экземпляр типа 4[8][14] | Цветочная пятиугольная мозаика Экземпляр типов 1, 2 и 5 |
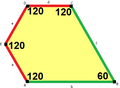
 120°, 120°, 120°, 90°, 90° V3.3.3.4.4 | 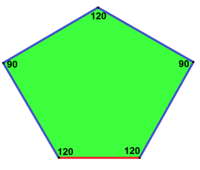 120°, 120°, 90°, 120°, 90° V3.3.4.3.4 | 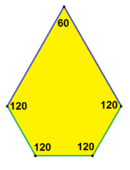 120°, 120°, 120°, 120°, 60° V3.3.3.3.6 |
Замощение плоскости несколькими плитками
[править | править код]Паркеты, двойственные k-однородным
[править | править код]Другие k-однородные паркеты, все вершины которых имеют по пять исходящих рёбер, также имеют двойственные пятиугольные паркеты, но состоящие из нескольких разных плиток. Однако никаких других плиток кроме трёх, фигурирующих в обычных паркетах, двойственных однородным, в них не появляется.
Паркеты, двойственные k-однородному, являются k-изоэдральными.
Ниже для примера приведены пятиугольные паркеты, двойственные 2,3,4 и 5-однородным, а также отдельно (ниже каждого) — плитки, составляющие их.
| 2-изоэдральные | 3-изоэдральные | |||
|---|---|---|---|---|
| p4g (4*2) | pgg (22×) | p2 (2222) | p6 (*632) | |
 |  |  |  |  |
| 4-изоэдральные | 5-изоэдральные | |||
| pgg (22×) | p2 (2222) | p6m (*632) | ||
 |  |  |  |  |
| 5-изоэдральные | ||||
| pgg (22×) | p2 (2222) | |||
 |  |  |  |  |
Пятиугольно-шестиугольные мозаики
[править | править код]
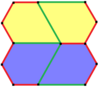
Пятиугольники находятся в интересных соотношениях с шестиугольниками. Некоторые виды шестиугольников могут быть разбиты на пятиугольники — в частности, отдельный шестиугольник может быть разбит на:
- 2 плитки типа 1
- 3 плитки типа 3
- 4 плитки типа 4
- 9 плиток типа 3
Вследствие такого разнообразия возможностей, плоскость может быть разбита на пятиугольники бесконечным числом способов, генерируемых из подразбиения шестиугольников регулярной мозаики.
Замощение невыпуклыми пятиугольниками
[править | править код]Замощения плоскости невыпуклыми многоугольниками также существуют. Один из таких примеров — мозаика «Сфинкс», непериодическое замощение через наращивание размера делящейся плитки. Для фигуры «Сфинкс» существует также и периодическое замощение через сборку их пар в параллелограммы и тривиальное замощение плоскости такими параллелограммами.
В 2003 году Гервер показал, как правильный треугольник можно разбить на три невыпуклых многоугольника. Пользуясь той же схемой, можно бесконечным числом способов разбить любой правильный -угольник на невыпуклых пятиугольников. В частности, этот способ подходит для 3, 4 и 6-угольников, через подразбиение регулярных мозаик которых можно таким образом генерировать ещё один бесконечный класс разбиений плоскости на невыпуклые многоугольники.
Примечания
[править | править код]- ↑ Коняев, Андрей (2017-07-12). "Французский математик решил задачу о замощении плоскости". N+1. Архивировано 5 января 2018. Дата обращения: 4 января 2018.
- ↑ Препринт работы Рао. Дата обращения: 12 марта 2018. Архивировано 2 августа 2017 года.
- ↑ Код программы Хейлза
- ↑ Публикация о работе Хейлза Архивная копия от 6 августа 2017 на Wayback Machine на сайте Quanta Magazine[англ.]
- ↑ Омский алгебраический семинар. Дата обращения: 12 марта 2018. Архивировано 12 марта 2018 года.
- ↑ О. Г. Багина. О свойствах мозаичных пятиугольников с парой равных смежных сторон // Институт математики им. С. Л. Соболева СО РАН Сибирские электронные математические известия. — Электронный журнал, 2017. — 8 декабрь (т. 14). — С. 1380—1412. — doi:10.17377/semi.2017.14.119. Архивировано 12 марта 2018 года.
- ↑ Sugimoto, Teruhisa (2012), "Convex pentagons for edge-to-edge tiling, I.", Forma, 27 (1): 93—103, MR 3030316, Архивировано из оригинала 20 мая 2020, Дата обращения: 12 марта 2018
{{citation}}: Недопустимый|ref=harv(справка) - ↑ 1 2 3 Reinhardt, Karl (1918), Über die Zerlegung der Ebene in Polygone, Dissertation Frankfurt am Main (нем.), Borna-Leipzig, Druck von Robert Noske, pp. 77—81
{{citation}}: Википедия:Обслуживание CS1 (лишняя пунктуация) (ссылка) (замечание: в работе присутствует как минимум одна ошибка — сумма углов γ+δ в первых двух типах плиток на странице 77 должна быть равна π, а не 2π) - ↑ Grünbaum, Shephard, 1978.
- ↑ Schattschneider, 1978.
- ↑ Mann, Casey; McLoud-Mann, Jennifer; David Von Derau (2015). "Convex pentagons that admit $i$-block transitive tilings". arXiv:1510.01186 [math.MG].
- ↑ Klaassen, Bernhard. Rotationally symmetric tilings with convex pentagons and hexagons (англ.) // Elemente der Mathematik[англ.] : journal. — 2016. — Vol. 71, no. 4. — P. 137—144. — ISSN 0013-6018. — doi:10.4171/em/310.
- ↑ Klaassen, Bernhard (2016). "Rotationally Symmetric Tilings with Convex Pentagons and Hexagons". arXiv:1509.06297 [math.MG].
- ↑ Cairo pentagonal tiling generated by a pentagon type 4 query Архивная копия от 28 декабря 2017 на Wayback Machine and by a pentagon type 2 tiling query Архивная копия от 29 декабря 2017 на Wayback Machine on wolframalpha.com Архивная копия от 24 февраля 2011 на Wayback Machine (caution: the wolfram definition of pentagon type 2 tiling does not correspond with type 2 defined by Reinhardt in 1918)
Ссылки
[править | править код]- Branko Grünbaum, Geoffrey C. Shephard. Isohedral tilings of the plane by polygons // Commentarii Mathematici Helvetici. — 1978. — Т. 53. — С. =542—571. — ISSN 0010-2571. — doi:10.5169/seals-40786. (недоступная ссылка)
- Schattschneider, Doris (1978), "Tiling the plane with congruent pentagons", Mathematics Magazine, 51 (1): 29—44, doi:10.2307/2689644, ISSN 0025-570X, MR 0493766
{{citation}}: Неизвестный параметр|jstуууууor=игнорируется (справка) - Gerver, M. L. (2003), "Theorems on tessellations by polygons", Sbornik: Mathematics, 194 (6): 879—895, Bibcode:2003SbMat.194..879G, doi:10.1070/sm2003v194n06abeh000743
- Pentagon Tilings
- Математики нашли новый тип пятиугольного паркета
- Математический паркет